 |
PROBLEMAS
DE RELATIVIDAD EN BACHILLERATO RESUELTOS COMO
INVESTIGACIÓN (1) |
 |
|
|
|
Problemas de
relatividad (cinemática) con
enunciado abierto, resueltos como actividad de investigación
usando conceptos del programa oficial de 2º Bachillerato.
La teoría básica sobre relatividad especial se puede
consultar
aquí.
|
|
|
Realizados por Manuel
Alonso Sánchez, Jaime Carrascosa Alís y
Salvador Martínez Sala |
|
|
|
|
Problemas de cinemática
relativista |
|
|
|
 |
|
 |
|
Enunciado: Desde una nave que se está
alejando de la Tierra se emite un haz de
partículas ¿Qué velocidad tiene ese haz con
respecto a la Tierra? (Aplicad el resultado
obtenido a diferentes supuestos, considerando
que las partículas se emitan en uno u otro
sentido, que su velocidad sea relativamente
pequeña o comparable con la velocidad de la luz
o que lo que se emita sea, por ejemplo, un haz
de luz láser para comunicarse con con la Tierra) |
|
|
|
|
|
 |
|
 |
|
Enunciado: Durante el año 2017 el
telescopio espacial Kepler descubrió que
alrededor de la estrella catalogada como GJ 9827
orbitan tres planetas similares a la Tierra. ¿A
qué velocidad tendría que viajar una nave
intergaláctica para llegar a uno de esos
planetas, situado a 100 años luz de la Tierra y
que sus tripulantes pudieran confirmar la
posibilidad de establecer allí una colonia
terrestre? |
|
|
|
|
|
|
 |
|
 |
|
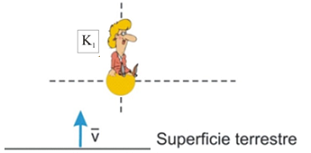
Enunciado: Una partícula subatómica en
reposo en un SRI (K1) se desintegra
espontáneamente con un periodo de semi-desintegración
determinado. ¿Cuánto valdrá dicho periodo cuando
el mismo se mida desde otro SRI (K2) respecto
del cual la partícula se desplaza con velocidad
constante? |
|
|
|
|
|
|
 |
|
 |
|
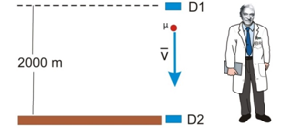
Enunciado: En su histórico experimento
los científicos Rossi y Hall colocaron un
detector de muones a 2000 m de altura (D1) y
otro al nivel del mar (D2). De esta forma
pudieron comprobar que el número de muones
registrados por el detector D1 era de 563 muones/hora.
De acuerdo con la teoría de la relatividad
¿cuántos muones por hora debieron registrar en
el detector D2? |
|
|
|
|
|
|
 |
|
 |
|
Enunciado: Se determina por métodos
ópticos la longitud de una nave espacial que
pasa por las proximidades de la Tierra
obteniendo un valor de 100 m. En contacto
radiofónico los astronautas que viajan en la
nave comunican que la longitud de su nave es de
120 m. Considerando Tierra y nave como sistemas
de referencia inerciales, determinad la
velocidad (módulo) con que la nave se desplaza
respecto de la Tierra. |
|
|
|
|
|
|
 |
|
 |
|
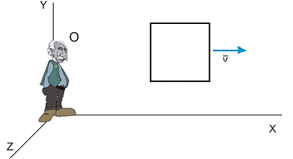
Enunciado: La longitud propia de cada uno
de los lados de un cuadrado es “a”. ¿Cuánto
valdrá su perímetro para un observador “O”
situado en un sistema de referencia inercial que
se aleja de dicho cuadrado a una velocidad
constante y en dirección paralela a uno de sus
lados? (Estudiad el resultado para los casos en
que v<<c y para cuando v tiende a
c) |
|
|
|
|
|
|
 |
|
 |
|
Enunciado: Una nave describe una órbita
circular a gran velocidad alrededor de un
determinado cuerpo celeste. ¿Cuánto vale en el
sistema de referencia de la nave el cociente (C)
entre la longitud (L) y el diámetro (D) de la
órbita? |
|
|
|