| |
|
 |
LEYES DE TRANSFORMACIÓN
RELATIVISTAS |
 |
|
|
|
| |
|
El carácter relativo de
los movimientos exige a toda teoría mecánica
dotarse de un conjunto de
ecuaciones adecuado para trasladar los valores de las
magnitudes que describen cada movimiento al pasar
de un sistema de referencia a otro. De acuerdo con los
hechos experimentales, dichas ecuaciones han de tener
ser compatibles con un límite superior de velocidad, c,
y han de mostrar una
adecuada ligazón en las coordenadas que dan el tiempo y
la posición. Todos estos requisitos los cumplen las leyes de transformación
de la teoría de la relatividad especial, o leyes de transformación de Lorentz-Einstein,
que, como todas las expresiones relativistas, se pueden
deducir operativamente de los
postulados de la relatividad.
|
| |
|
 |
|
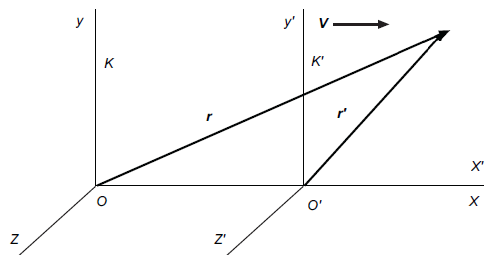
Así pues, las ecuaciones de Lorentz-Einstein relacionan
las coordenadas que dan la posición y el tiempo
de un móvil en un sistema de referencia
inercial, K (x, y, z, t) y en
otro
sistema de referencia inercial, K' (x',
y', z', t'), que tenga una velocidad, v, respecto de K.
|
| |
|
 |
|
El factor gamma que aparece en
estas ecuaciones depende del cociente entre la velocidad
relativa de los sistemas de referencia, v, y la velocidad de la luz, c,
según expresa la fórmula
siguiente:
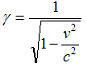 |
|
|
| |
|
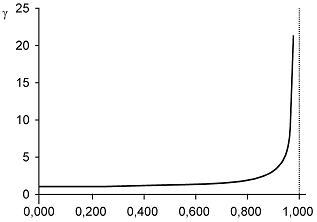
Es
importante fijarse en que este factor tiende a ser igual a uno
cuando la velocidad es pequeña comparada con la
velocidad de la luz, c, y que, para que aumente
significativamente, la
velocidad relativa entre los SRI que
alcanzar valores muy elevados (ver figura adjunta).
Esto implica que mientras las velocidades
son pequeñas en comparación
con la velocidad de la luz, las leyes de transformación
relativistas apenas se diferencian de las de la mecánica
de Newton y es aplicable el
principio de relatividad de Galileo. Así ocurre en muchos movimientos y experiencias cotidianas (el movimiento de un proyectil,
un viaje en tren o en avión, etc.). Por eso, en estos casos, es legítimo
usar la mecánica de
Newton, pues dicha teoría produce resultados que
apenas se desvían de los más correctos
que proporcionan las leyes de la
relatividad. |
|
 |
|
|
|
|
| |
|
|
| |
En otros casos,
la aplicación de las leyes relativistas es obligada, ya que esas
grandes velocidades si son habituales, por ejemplo, en la física
nuclear y en la física de partículas, donde las radiaciones y
los "vuelos" de partículas subatómicas tienen velocidades
comparables con la velocidad de la luz, c. |
|
| |
|
|
| |
| |
Índice |
 |
|
|
|
| |
|
|
|

