EL ESPACIO-TIEMPO

 

Para introducir este concepto central de la relatividad se puede pensar en un objeto que tenga una determinada velocidad respecto de un sistema de referencia, K. El mismo objeto tiene una velocidad mayor respecto de cualquier otro sistema de referencia K´, que se mueva alejándose de K en sentido opuesto. Esa velocidad es aún mayor respecto de un tercer sistema de referencia K´´, que se aleje de K´, del mismo modo. Y así sucesivamente. El cociente entre los desplazamientos espaciales y los correspondientes intervalos de tiempo del objeto respecto de cada uno de estos sistemas de referencia es su velocidad media en ellos.

 

Ahora bien, como el objeto no puede alcanzar el límite superior de velocidad, este cociente no puede tomar cualquier valor arbitrariamente grande. Por tanto, las distancias espaciales y los intervalos temporales del movimiento del objeto han de ser interdependientes y dependientes del sistema de referencia. Por ello, en lugar de hablar del espacio y/o del tiempo por separado, procede concebir un entramado espacio-tiempo.

Para formalizar este concepto, se define un vector, ds, de cuatro dimensiones (una temporal y tres espaciales) con origen en un punto del espacio-tiempo (x1, y1, z1, ct1) y final en otro (x2, y2, z2, ct2). Este vector [ds = (c·dt, dx, dy, dz)] se llama cuadrivector espacio-tiempo, y usando las leyes relativistas se constata que su módulo, ds [cuyo cuadrado es: (ds)2 = (cdt)2-(dx)2-(dy)2-(dz)2] es una magnitud invariante en esta teoría, lo que significa que tiene el mismo valor en cualquier sistema de referencia inercial y se escribe igual en todos ellos. Se llama a esta magnitud invariante, ds, intervalo o distancia en el espacio-tiempo.

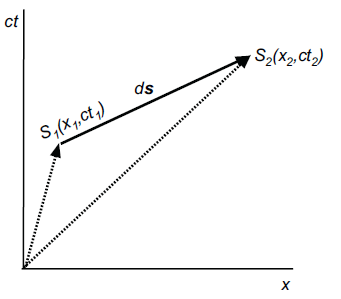
En el esquema adjunto (a la derecha) se representa el vector ds en un diagrama de ejes coordenados que considera una de las tres dimensiones espaciales (x) y la dimensión temporal (c·t).

 

 

Conviene fijarse en el signo negativo de la expresión que define la distancia en el espacio tiempo, pues implica que cuanto mayor sea la longitud de un desplazamiento espacial realizada por un móvil con respecto a un determinado sistema de referencia inercial, mayor es el tiempo que se mide en él de ese movimiento. Esto ocurre así porque el cociente entre ese desplazamiento y ese tiempo es la velocidad del móvil y ésta, por mucho que aumente (al cambiar de sistema de referencia), no puede alcanzar la velocidad límite.

 

 

En esta animación se representa el cuadrivector espacio-tiempo del movimiento de una partícula con respecto a dos sistemas de referencia inerciales (SRI): El SRI propio, ligado a la partícula (con respecto al cual dicha partícula está en reposo) y otro SRI diferente, respecto del que la partícula tiene una cierta velocidad, v.

Se puede modificar el valor de v (lo que equivale a cambiar de sistema de referencia) y comprobar que cuanto mayor sea v, mayor es la longitud aparente del cuadrivector en esta representación abstracta.

Clic aquí para descargar esta animación. Para usarla en tu ordenador, descarga Modellus

 

Índice