| |
|
 |
CUADRIVECTOR IMPULSO-ENERGÍA |
 |
|
|
|
|
|
|
Para transitar de la cinemática a la dinámica
relativista se define un
cuadrivector dinámico, P,
multiplicando
la masa de la partícula,
m,
por una velocidad en el
espacio-tiempo
(igual al
cociente entre el
desplazamiento en el espacio-tiempo,
ds,
y el tiempo propio correspondiente a ese
desplazamiento
dt0): |
|
|
|
P = m · ds/dt0 |
|
|
|
Este cuadrivector
dinámico, P, es proporcional al
cuadrivector espacio-tiempo
de la cinemática, ya que la masa m y el intervalo de
tiempo propio, dt0 son magnitudes invariantes en
relatividad, es decir, tienen el mismo valor con
independencia de cual sea el sistema de referencia (inercial)
que se adopte. |
|
|
|
Para entender el significado físico de este
vector dinámico, P, se ha de tener en cuenta que su primera componente (proporcional al
tiempo) es escalar y multiplicada por c, tiene
dimensiones de energía, E, mientras que las otras tres
componentes (proporcionales a
las tres coordenadas espaciales) forman en conjunto un
vector que tiene dimensiones de impulso o cantidad de
movimiento, p. Por todo ello, el vector dinámico
se denomina cuadrivector impulso-energía y se acostumbra
a expresar (él y sus componentes) en unidades de energía, es decir P (en
unidades de energía) = P·c = (E, p·c) |
|
|
|
Teniendo todo esto en cuenta, se obtienen
fácilmente (se pueden consultar
aquí
los desarrollos)
las expresiones de
la energía, E, del impulso, p y del cuadrivector
impulso-energía, P, que se expresan como
vemos en el cuadro adjunto. |
|
|
Cuadrivector impulso-energía |
P = (E, p·c) (en unidades de
energía) |
|
Energía |
E = m·c2·γ |
|
Impulso |
p = m·γ·v |
|
|
|
|
|
Por otra parte, puesto que, como se acaba
de ver, el cuadrivector
impulso-energía (dinámico) es proporcional al cuadrivector
desplazamiento
espacio-tiempo (cinemático), ambos vectores (cinemático
y dinámico) tienen la misma métrica y también ocurre que
el modulo de ambos es invariante. |
|
|
|
 |
|
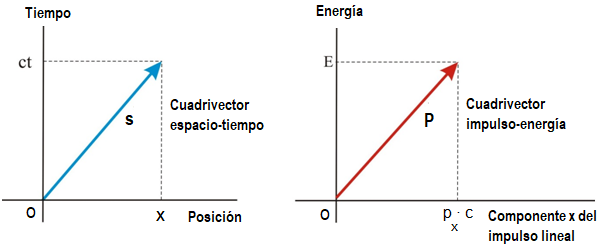
Estas
propiedades hacen que el cuadrivector
dinámico, P, se pueda representar en un diagrama
impulso-energía semejante al diagrama
espacio-tiempo que se usa para representar el cuadrivector cinemático,
ds.
Para una
determinada partícula (de masa m), y con
respecto a un determinado sistema de referencia
inercial, ambos vectores (representado cada uno
de ellos en su correspondiente diagrama) tienen la
misma orientación y sus longitudes son
proporcionales. |
|
|
|
|
Finalmente, también
resulta útil e interesante
representar en dinámica el cuadrivector de una partícula
usando un diagrama múltiple que considere diferentes
sistemas de referencia con respecto a los cuales, esa
partícula, tendrá velocidades diferentes. |
|
|
|
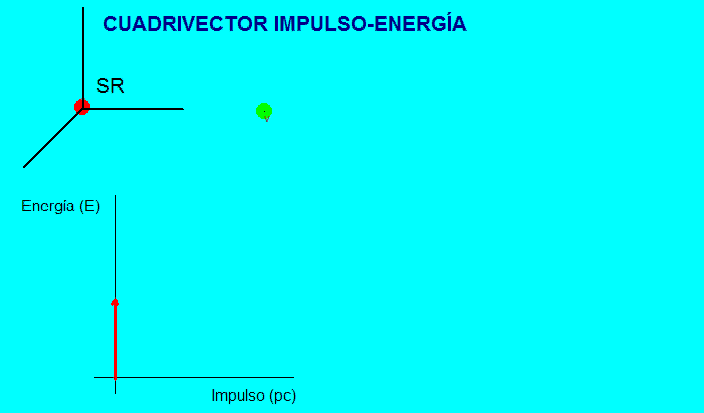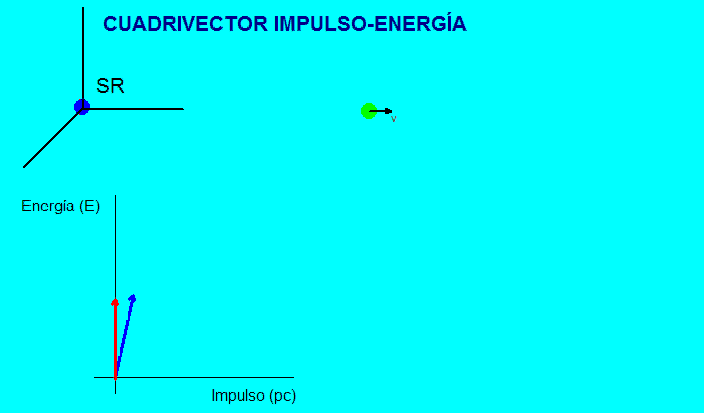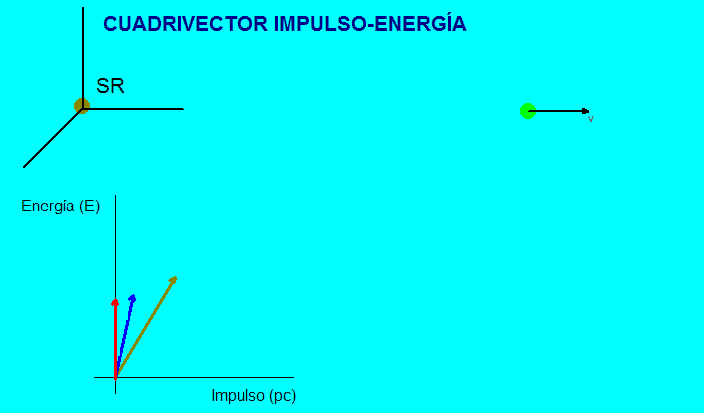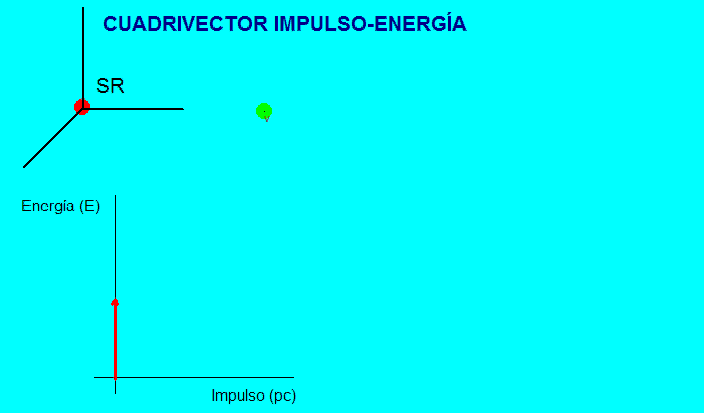
La animación
adjunta muestra esta representación.
En
el
sistema de referencia propio (ligado a la partícula), el
vector dinámico es vertical en el diagrama y, en
cualquier otro sistema de referencia se inclina y
aumenta su longitud aparente (tanto más cuanto mayor sea
la velocidad de la partícula).
Como es lógico, la métrica
que rige sobre estos vectores dinámicos, es
la misma que tienen los vectores cinemáticos y deriva
del hecho de que la partícula no pueda alcanzar el límite superior de
velocidades, c.
Clic
aquí
para
descargar esta animación.
Para usarla en tu
ordenador, descarga
Modellus |
|
 |
|
|
|
| |
|
|
| |
| |
Índice |
 |
|
|
|
| |
|
|
|
|
|
|