Dilatación de tiempos y contracción de longitudes

"DILATACIÓN DE TIEMPOS" Y "CONTRACCIÓN DE LONGITUDES"

Dos de las leyes importantes de la cinemática relativista, que corresponden al cambio entre sistemas inerciales, son la ley de dilatación del tiempo y la ley de contracción de la longitud. En realidad, como veremos ahora, son dos caras de la misma moneda, ya que muestran dos aspectos del mismo hecho físico.

Ley de dilatación del tiempo

La ley de dilatación del tiempo relaciona el intervalo de tiempo (que puede corresponder a la duración que tiene un proceso físico) en dos sistemas de referencia. Su expresión operativa es la siguiente:

Dt = gDt₀ siendo

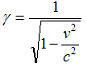En esta expresión el subíndice ₀ indica que nos referimos al intervalo de tiempo propio. El tiempo propio es una magnitud fundamental en relatividad y se define como el tiempo que registra un reloj transportado por un objeto en movimiento arbitrario; es una propiedad absoluta del movimiento del objeto, y por tanto, del reloj en ese movimiento. Así, el tiempo propio coincide con la coordenada t de un SRI cuando el reloj está en reposo en ese SRI y operacionalmente, podríamos usar ese reloj de ese sistema de referencia para medirlo. Así podemos decir que el intervalo de tiempo propio, Dt₀, que pueda corresponder a la duración de un proceso físico, es el que se determina en el sistema de referencia respecto del cual el origen y el final de dicho proceso ocurren en la misma posición. En cualquier otro sistema de referencia, los eventos que corresponden al origen y al final de ese mismo proceso no suceden en la misma posición y su duración tiene un valor diferente, Dt. Como g >1 lo que expresa la ley de dilatación del tiempo es que Dt > Dt₀ .

Es esencial que quede claro que esta discrepancia entre el valor de los tiempos referidos a un mismo proceso físico en dos sistemas de referencia distintos, no significa, de ninguna manera, que le pase nada al tiempo propio de cualquier proceso, aquel que puede medirse con un reloj en el sistema de referencia respecto del cual el origen y el final de ese proceso tienen la misma posición espacial. Con el concepto de espacio-tiempo en la mano, que se ha desarrollado anteriormente, debemos desprendernos de la concepción newtoniana del tiempo (un tiempo absoluto) y sustituirla por el mencionado entramado espacio-tiempo. Entonces, en este marco relativista, llegamos a la conclusión fundamental de que en la ley anterior, mientras el tiempo propio Dt₀ correspondiente a la duración de un proceso que ocurre en reposo respecto a un determinado SRI y se puede medir con un reloj de dicho SRI, el tiempo Dt que corresponda a la duración de ese mismo proceso en otros SRI se puede inferir usando la ley anterior, pero no medirse en ellos. Por este motivo, la expresión "dilatación de tiempos" para referirse a esta ley es muy desafortunada (aunque seguiremos usándola, si bien, desde ahora entrecomillada, ya que así se conoce esta ley) y podría inducirnos a malinterpretar el significado de esta ley, ya que es fuerte la tentación de olvidar el hecho fundamental de el tiempo no existe con independencia del espacio, sino que espacio y tiempo son inseparables.

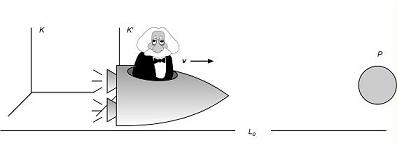
Podemos concretar un poco más e ilustrar la ley de "dilatación de tiempos" imaginando un viaje de una nave desde la Tierra hacia un planeta lejano, P. Los viajeros pueden medir la duración de este viaje con su reloj obteniendo el intervalo de tiempo propio del mismo en el sistema de referencia ligado a ellos (K´). Si consideramos a la Tierra y al planeta lejanos en reposo en un cierto SRI (K), respecto del cual los viajeros y su sistema de referencia (K´) se mueven con la velocidad v (esta aproximación implica despreciar la aceleración de ambos astros y proponer que la distancia entre ellos sea constante), podemos aplicar la ley de "dilatación de tiempos" entre estos dos SRI, y así concluimos que la duración del viaje es mayor en K que en K´.

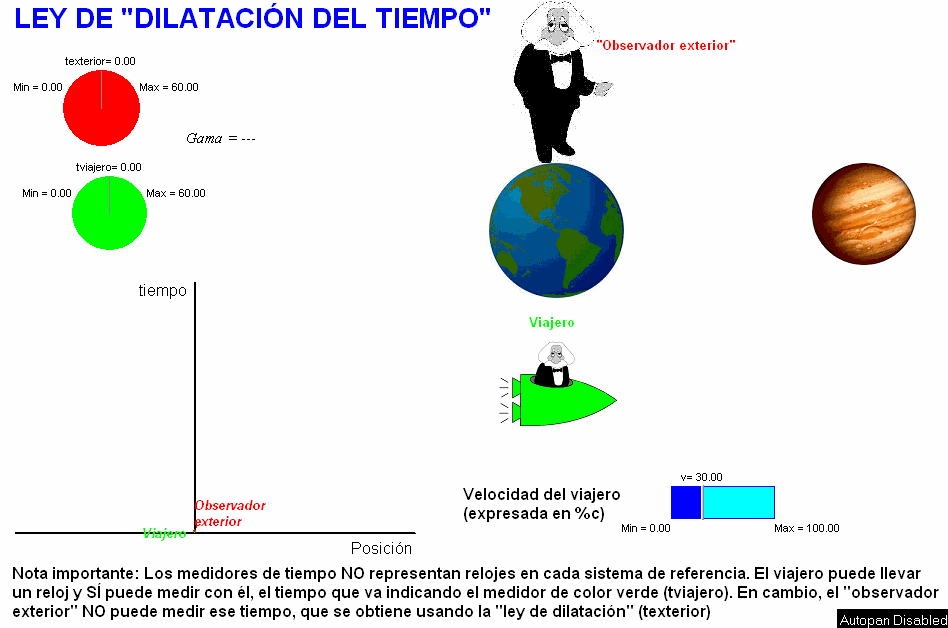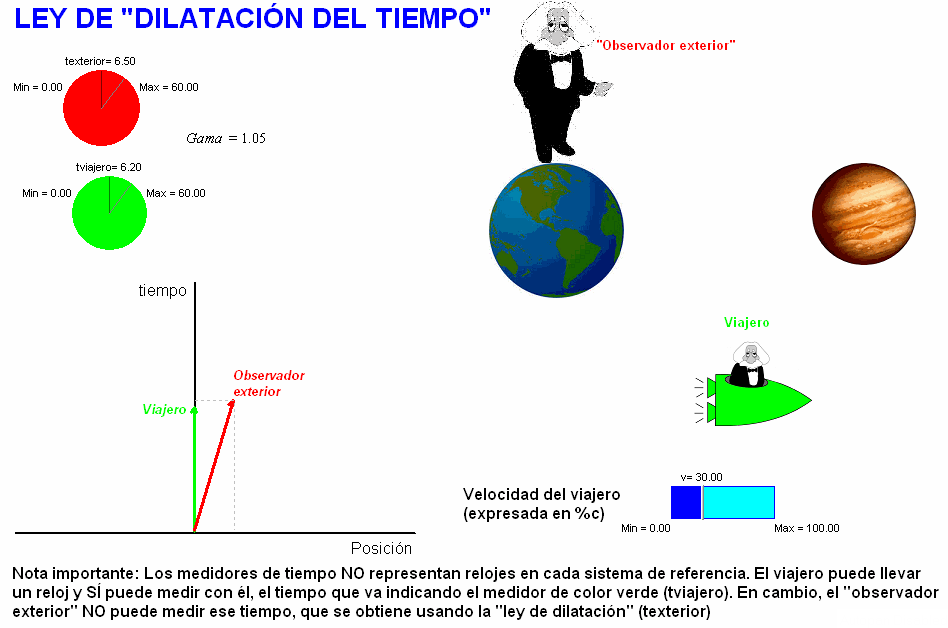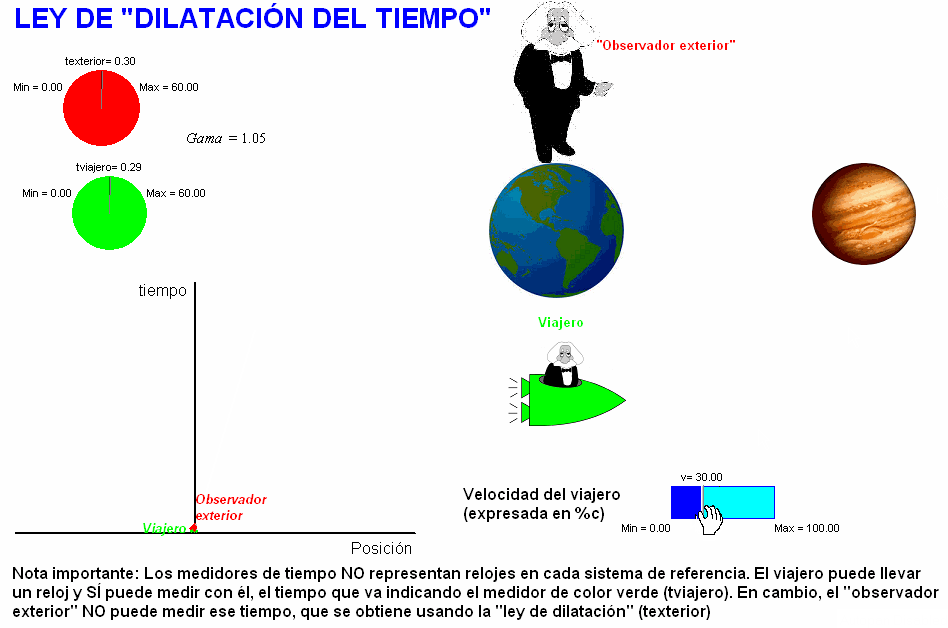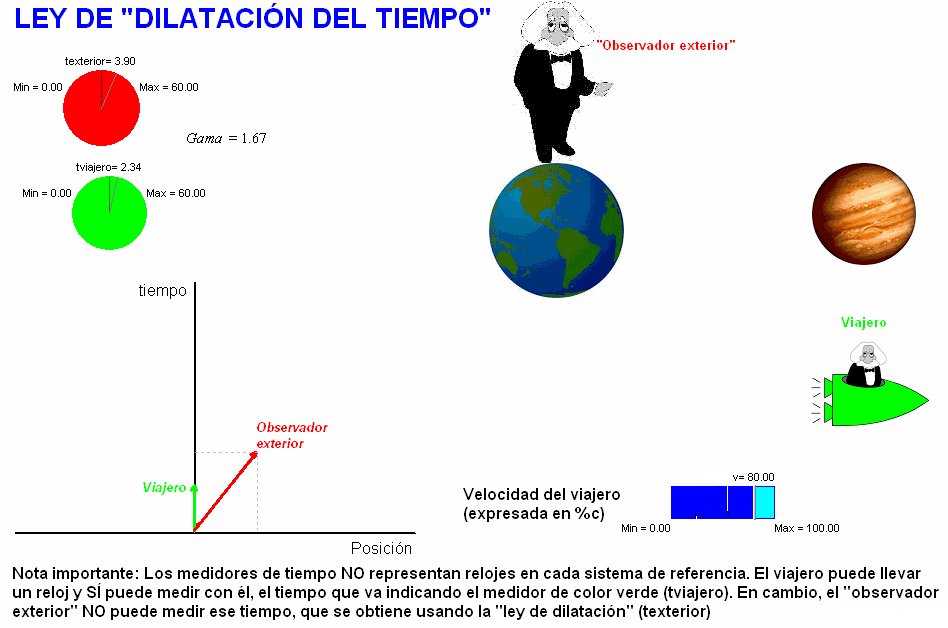
La animación adjunta (debajo) simula este viaje hipotético. En la pantalla se va dibujando el vector espacio-tiempo del viaje según el punto de vista de ambos sistemas de referencia y se calcula la duración del viaje para los viajeros (que ellos mismos pueden medir con su reloj) y para los habitantes de la Tierra (que pueden deducir usando la ley anterior, si, de algún modo, tienen conocimiento de la duración propia del viaje). El usuario puede modificar la velocidad del viaje y comprobar que la dilatación del tiempo resulta mayor cuanto mayor sea la velocidad de la nave.

Obsérvese en dicha animación la nota que nos recuerda no se ha de incurrir en el error de suponer que los medidores de tiempo (de color verde y rojo) pudieran representar sendos relojes en cada sistema de referencia. Como ya debemos saber, el único reloj real que se podría equiparar aquí con alguno de estos dos medidores es uno que lleve el viajero montado en la nave consigo, quien sí podría usarlo para medir la duración (propia) de su viaje, es decir, tviajero. En cambio, el "observador exterior" no puede medir con un reloj suyo la duración de ese viaje que él no realiza y, en este sentido, el término "observador exterior", también es desafortunado. El valor de la duración del viaje en el sistema de referencia ligado a la Tierra es inferido. Se obtiene aplicando las leyes de la relatividad.

Clic aquí para descargar esta animación. Si no lo tienes instala Modellus 2.5 (32 bits) o Modellus 3 (64 bits)

Ley de contracción de la longitud

Para llegar a expresar la ley de contracción de la longitud, seguimos analizando el ejemplo de este viaje hipotético, pero ahora lo hacemos según el punto de vista de los viajeros, es decir, con respecto al sistema de referencia ligado a la nave. En ese sistema de referencia el viaje se interpreta como un movimiento de la Tierra y del planeta en sentido opuesto a la misma velocidad v.

La distancia espacial entre la Tierra y el planeta es una longitud entre dos objetos que están en reposo en el sistema de referencia ligado a la Tierra, pero en movimiento en el sistema de referencia ligado a la nave. Por tanto, los viajeros se ven obligados a interpretar el mismo hecho físico, afirmando que esta distancia es menor en su sistema de referencia que el valor que tiene en el sistema de referencia en el que ambos astros están en reposo o longitud propia, la cual pueden medir los habitantes de la Tierra. Este razonamiento conduce directamente a expresar la también mal llamada ley de la "contracción de longitudes":

L= L₀/g siendo

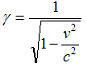En esta ley el subíndice ₀ vuelve a indicar que nos referimos a una longitud propia, que podemos expresar como el intervalo espacial entre dos posiciones en el sistema de referencia en el que dichas posiciones están en reposo. Siendo g >1 lo que expresa la ley de contracción de la longitud es que L< L₀.

La definición estandard de la longitud propia en relatividad es bastante más delicada que la anteriormente expuesta del tiempo propio, pero para entender la esencia de la ley de la contracción de la longitud, es suficiente con que se vea, como acabamos de decir, que es el reverso de la ley de dilatación del tiempo. Así hemos visto, en el ejemplo del hipotético viaje, que lo que se interpreta en el sistema de referencia ligado a la Tierra y a planeta lejano como una "dilatación del tiempo" (la duración del viaje es mayor para los terrestres que para los viajeros), en el sistema de referencia ligado a la nave se interpreta como una "contracción de longitud" (la distancia entre la Tierra y el planeta es menor para los viajeros). Ambas son interpretaciones locales de un mismo hecho, que lógicamente es consecuencia de la ligazón espacio-tiempo en el mundo real (relativista) donde existe un límite superior de velocidades y donde, como ya sabemos (y esta es la clave), el módulo del intervalo espacio-tiempo es invariante se escribe igual y vale lo mismo en todos los sistemas de referencia.

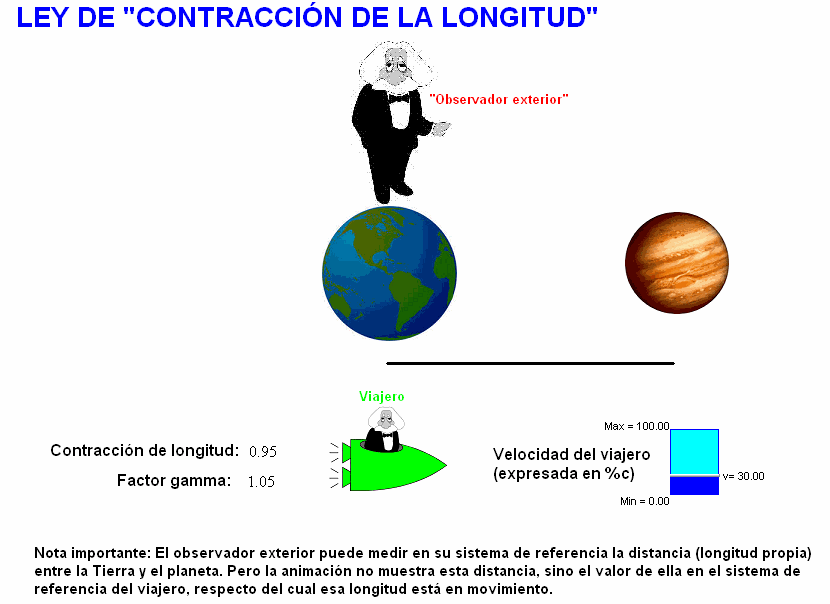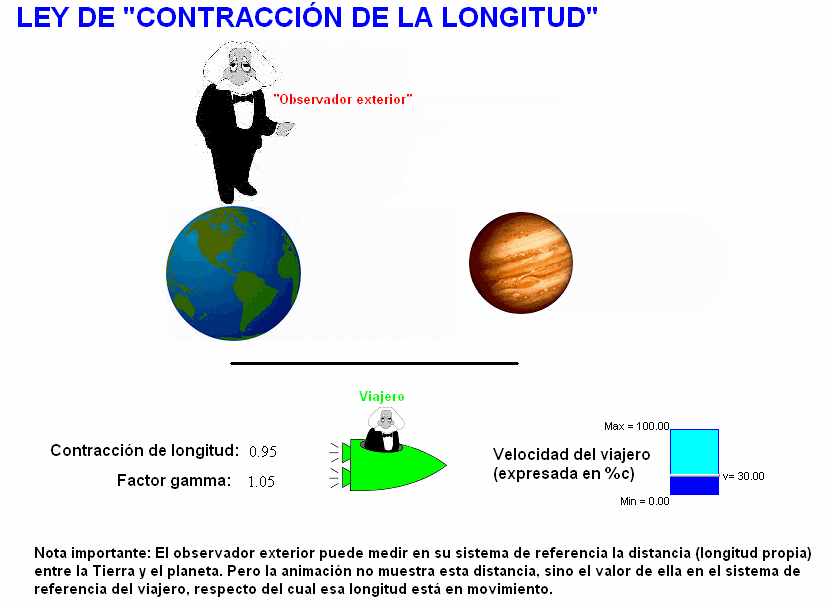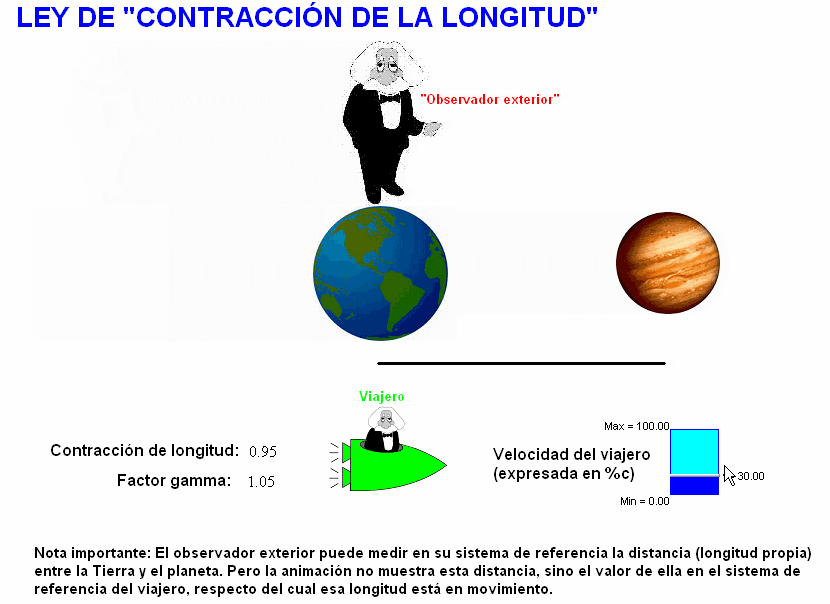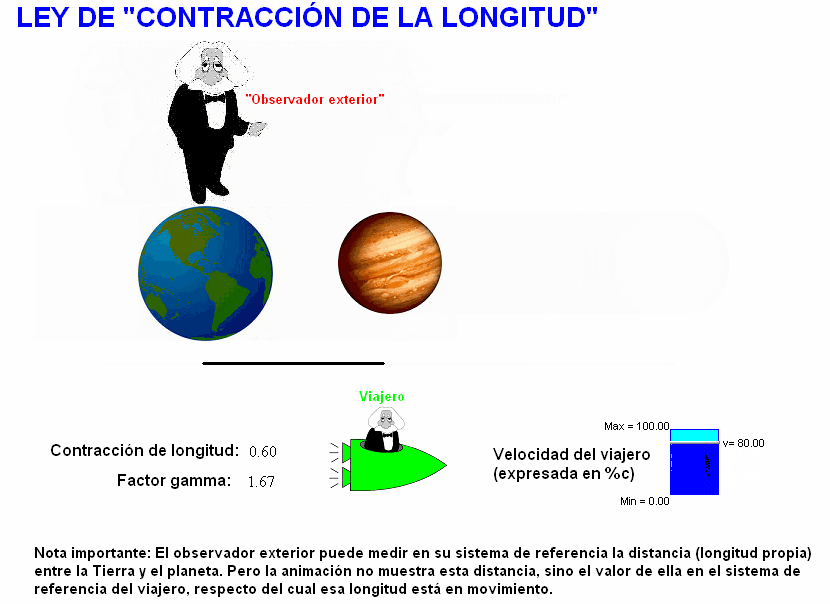
Esta otra animación simula el mismo viaje anterior según este punto de vista que obtiene una contracción de la longitud de una varilla con origen en la Tierra y extremo en el planeta. Manipulándola, se puede modificar la velocidad de la nave (con respecto a la Tierra y el planeta) y ver que ello se traduce en una contracción mayor o menor de esa longitud.

Clic aquí para descargar esta animación. Si no lo tienes instala Modellus 2.5 (32 bits) o Modellus 3 (64 bits)

También aquí hay que fijarse en la nota que nos recuerda que la separación entre la Tierra y el planeta que, como vemos, se dibuja diferente dependiendo de la velocidad a la que ambos astros se mueven respecto del viajero, es una distancia que NO puede medir dicho viajero. El "observador exterior" sí que puede medir la longitud propia del viaje, es decir, la distancia entre la Tierra y el planeta, ya que ambos astros están en reposo en su sistema de referencia. Pero no es esta la distancia que se representa en la animación, sino la que corresponde al viaje según el punto de vista del viajero..

Hay que tener en consideración también el hecho de que la "contracción de la longitud" se produce únicamente en la dirección del movimiento, ya que, como hemos visto, es consecuencia de las propiedades del espacio-tiempo cuando nos desplazamos por él esa dirección. Si, por ejemplo, tuviéramos una varilla orientada verticalmente desplazándose (con respecto a un determinado sistema de referencia exterior) paralelamente a si misma en la dirección horizontal, su longitud (vertical) sería igual en el sistema de referencia ligado a ella y en el sistema de referencia exterior. Y, si esa varilla mantuviera una posición oblicua con respecto a la dirección en la que se desplaza, la contracción de longitud respecto del sistema de referencia exterior sería la de su proyección en la dirección del movimiento.

En este documento se deduce matemáticamente la ley de dilatación del tiempo por dos procedimientos diferentes: Usando el concepto de que el módulo del intervalo espacio-tiempo es invariante y usando "relojes de luz". En este otro documento se deduce la ley de la contracción de la longitud, a partir de la ley de dilatación del tiempo, por tanto, mostrando la interrelación entre ambas.