| |
|
 |
CAUSALIDAD |
 |
|
|
|
|
| |
|
|
| |
Se acaba
de ver que dos sucesos S1 y S2
pueden ser simultáneos en un cierto sistema de
referencia inercial, S1 anterior a S2
en otro sistema de referencia inercial y S2
anterior a S1 en un tercer sistema de
referencia inercial. Entonces, nos podemos plantear la
siguiente cuestión: ¿Se vulnera la causalidad de las
leyes físicas?, ¿podría ser en relatividad un suceso
(como, por ejemplo, un nacimiento) anterior a otro que
lo provocó (la correspondiente fecundación)?
|
|
| |
|
|
| |
|
 |
|
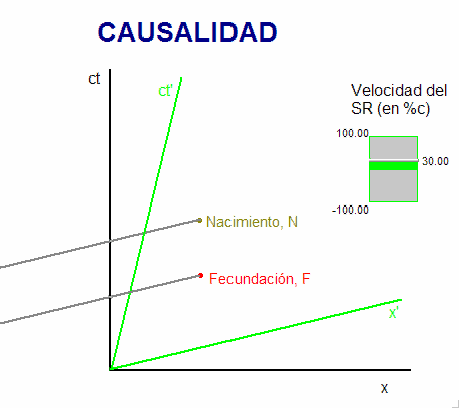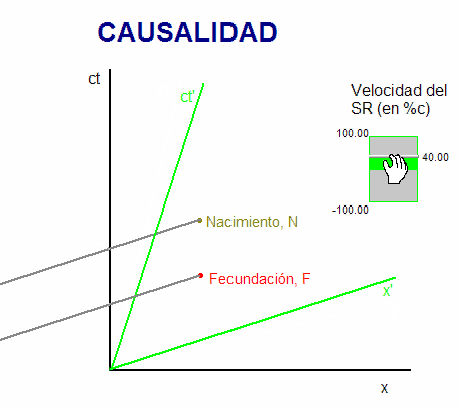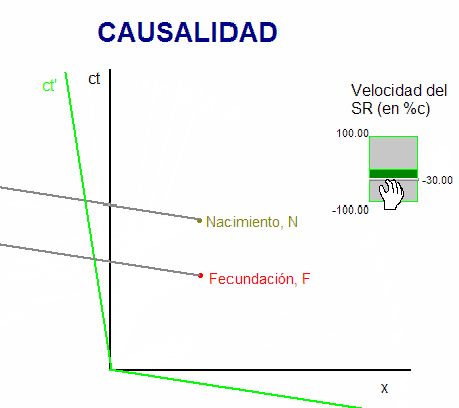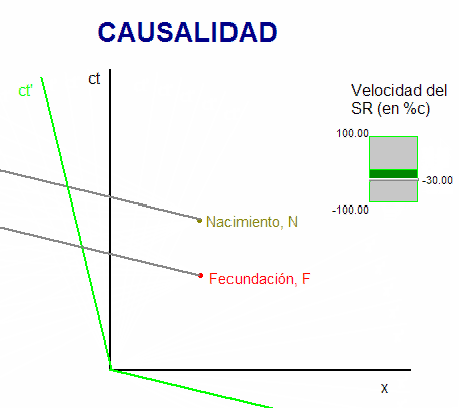
La animación adjunta resuelve esta cuestión usando un
diagrama múltiple que incluye dos
sistemas de referencia inerciales: Uno ligado a
la madre (ejes de color negro), en el que el
suceso del nacimiento, N, ocurre 9 meses después
que el de la fecundación, F. Otro (ejes de color
verde) cuya velocidad con respecto al sistema de
referencia ligado a la madre se puede modificar
(asignándole cualquier valor que no alcance el
límite superior, c).
Como se ve, al modificar la velocidad del
segundo sistema de referencia, varía la
inclinación de sus ejes coordenados en el
diagrama, y también varía
(respecto de ese sistema de referencia) el
tiempo transcurrido entre la fecundación y el
nacimiento. Pero en ningún caso se
altera el orden temporal entre estos dos
sucesos. Por tanto, se obtiene que la
fecundación es absolutamente anterior al
nacimiento, en consonancia con el principio de
causalidad de las leyes físicas (la causa es
siempre anterior al efecto).
Clic
aquí
para
descargar esta animación. Si no lo tienes instala
Modellus
2.5 (32 bits) o
Modellus 3 (64 bits) |
|
|
| |
|
|
| |
|
 |
|
Esta otra animación permite al usuario
desplazar el lugar del espacio-tiempo en el que sucede el
nacimiento, N, y puede ayudar a aclarar un poco más
estos conceptos. Vemos que es posible desplazar
N, manteniendo el hecho
de que en el sistema de referencia de la madre
(ejes de color negro) ocurra 9 meses después de
la fecundación, F, y logrando que en el otro
sistema de referencia (ejes de color verde)
dicho nacimiento, N, llegue a ser ser anterior a la
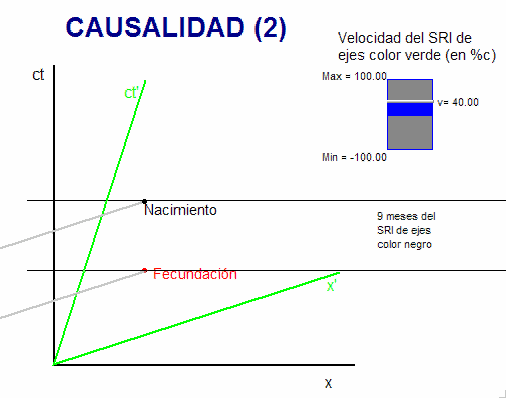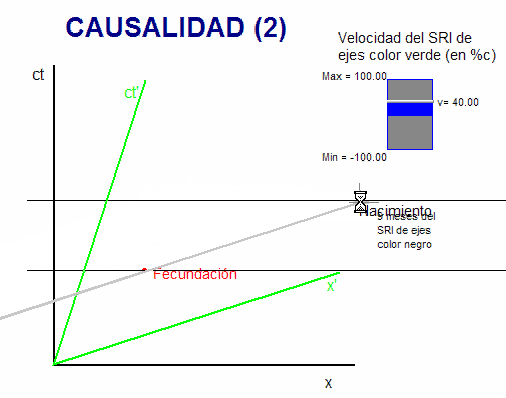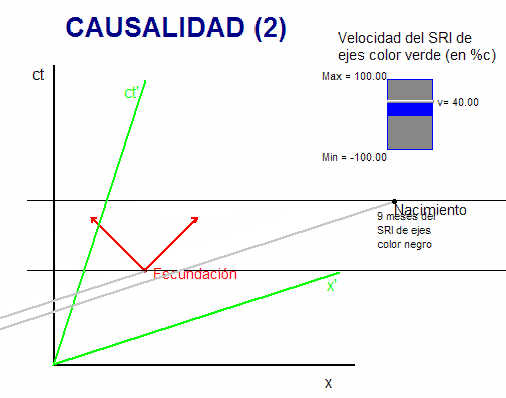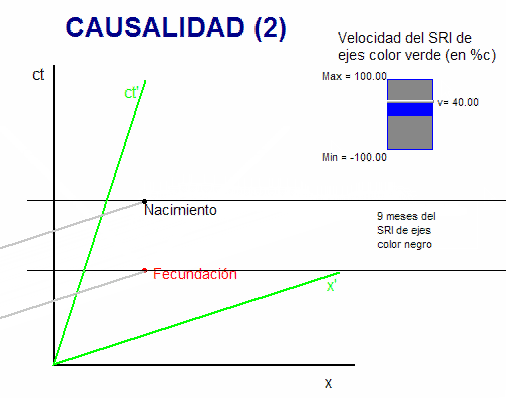
fecundación, F. ¿Se vulnera entonces el
principio de causalidad?. La respuesta vuelve a
ser NO, porque, como se ve, para que pueda tener
lugar esa inversión temporal entre los dos
sucesos, es necesario que el nacimiento, N,
quede fuera del cono de luz (representado en
color rojo) con origen en la fecundación, F.
Es decir, en ese caso, F y N no serían sucesos
ligados causalmente y N se situaría en el
diagrama en la zona que Minkowski denominó
presente de F u "otro lugar".
Clic
aquí
para
descargar esta animación. Si no lo tienes instala
Modellus
2.5 (32 bits) o
Modellus 3 (64 bits) |
|
|
| |
|
|
| |
A modo
de resumen diremos que entre dos
sucesos del espacio-tiempo, cabe considerar dos
posibilidades: a) Que se pueda establecer entre
ellos una relación causal. Entonces, uno de ellos es
absolutamente anterior al otro y ambos entran dentro un
mismo "cono de luz" en un diagrama espacio-tiempo. b)
Que no se pueda establecer una relación causal entre
ellos. Entonces, ambos son simultáneos en un determinado
sistema de referencia inercial, uno es anterior al otro
en otros referenciales y se invierte dicho orden
temporal en otros. En este caso, al representarlos en un diagrama
espacio-tiempo, no es posible ubicarlos dentro de un
mismo cono de luz. |
|
| |
|
|
|
|