| |
|
 |
LOS GEMELOS |
 |
|
|
|
|
| |
|
|
| |
La llamada
paradoja de los gemelos la protagonizan dos hermanos.
Uno hace un largo viaje de ida y vuelta a una estrella en una
nave espacial y el otro se queda en la Tierra. Considerando la
ley de la dilatación del tiempo (o, su reverso, la ley de
contracción de la longitud) la cuestión que se plantea es saber
cuando se encuentran de nuevo cuál es el gemelo más joven y cuál
el mas viejo. La paradoja surge a partir de las siguientes
observaciones: a) Según el punto de vista del gemelo que
se queda en Tierra, el tiempo que determina del viaje de su
hermano es impropio y, por tanto, cuando se encuentren de nuevo,
el gemelo que hizo el viaje ha de ser el más joven. b)
Según el punto de vista del gemelo que va dentro de la nave, el
que viaja, en realidad, es el gemelo en la Tierra y, por tanto,
cabría esperar que cuando vuelvan a encontrarse sea el gemelo
que en la Tierra quien haya envejecido menos. |
|
| |
|
|
| |
La formulación
más habitual de esta aparente paradoja se debe a
Paul Langevin (1872-1976)
y a Einstein le costó aclararla unos cuantos años, hasta
que formuló la relatividad general y demostró que es el gemelo
de la Tierra quien envejece más rápido. Sin embargo, aunque
Einstein la resolvió inicialmente en el contexto de la
relatividad general, la paradoja se puede resolver sin especial
dificultad dentro de los límites de la teoría de la relatividad
especial. Es más, en realidad no hay tal paradoja y ello es así
porque no
existe una verdadera simetría entre ambos gemelos, ya que sólo a uno de ellos se puede ligar a un sistema de referencia inercial. Ese
gemelo puede considerarse legítimamente en reposo y, si
así ocurre, el otro gemelo tendrá que acelerar como mínimo al
salir y al cambiar de sentido antes de regresar. En estas
condiciones, la aplicación de las leyes obtiene que el gemelo que queda en reposo (o con movimiento
rectilíneo y uniforme) es, sin lugar a dudas, el que envejece más
que su hermano viajero. |
|
| |
|
|
| |
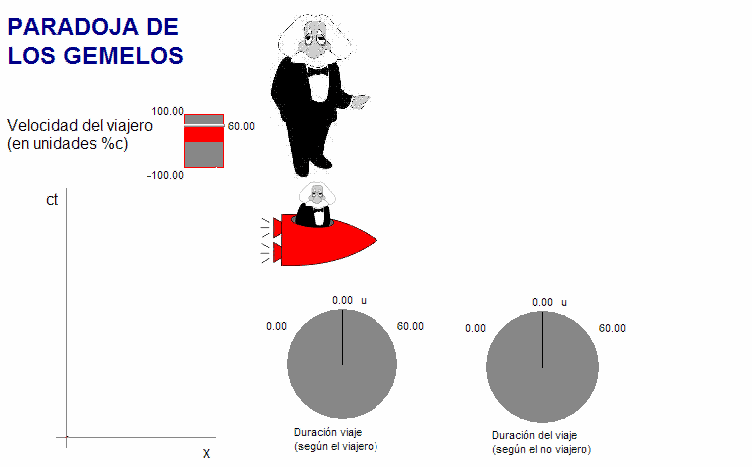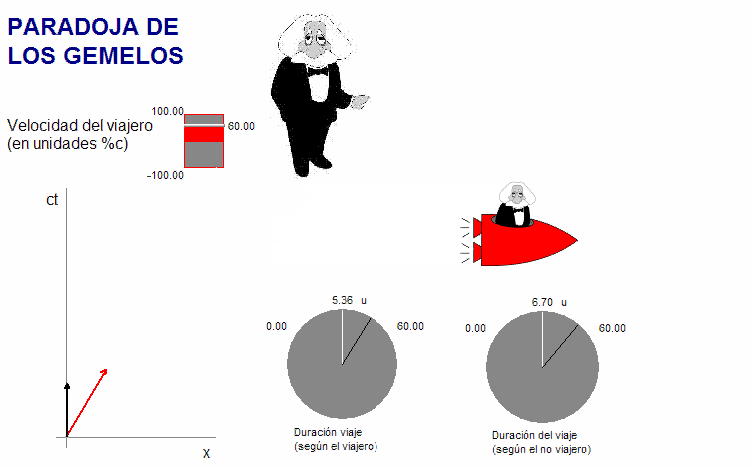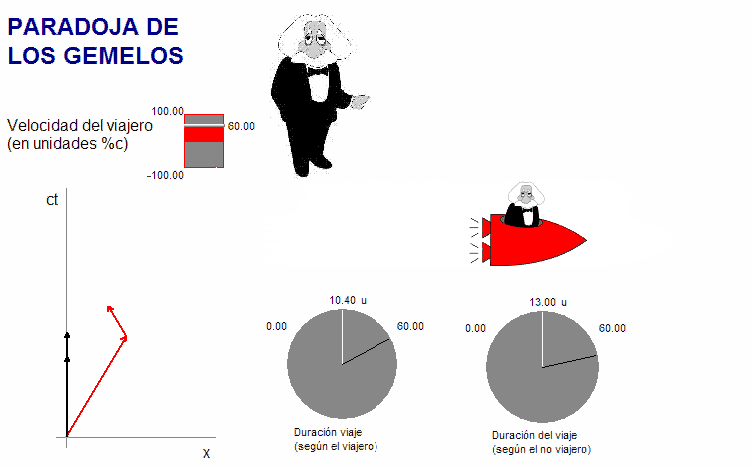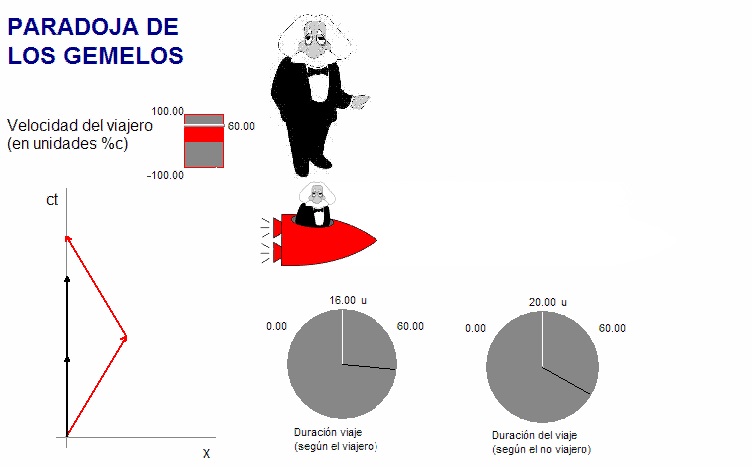
La
animación adjunta (debajo) representa el problema en un diagrama
espacio-tiempo dibujado en el sistema de referencia
inercial. Los cuadrivectores que corresponden al
gemelo inercial (color negro), son verticales (está en reposo),
mientras que los de su hermano viajero (color rojo) se inclinan y
aumenta su tamaño aparente, tanto más cuanto mayor la
velocidad de la nave. |
|
| |
|
|
| |
|
 |
|
En
consecuencia, el viaje del gemelo no inercial acaba en
un punto del diagrama situado más arriba que lo hace el
"no viaje" del gemelo inercial. Para que éste
alcance ese punto del diagrama tiene que esperar un
tiempo de su sistema de referencia igual al tramo que
falta en el diagrama. Es decir, lo recibirá siendo más
viejo.
Clic
aquí
para
descargar esta animación.
Para usarla en tu
ordenador, descarga
Modellus
Aclaración: Como
hicimos en animaciones similares anteriores conviene que
aquí también advertir de que al
usar esta animación hay que tener la debida
cautela para no incurrir en el error de pensar que los medidores de tiempo pudieran representar
relojes reales. El único reloj que se puede
equiparar en el proceso que se ilustra con esos
medidores es el que puede llevar el viajero
montado en la nave consigo, ya que con dicho
reloj el viajero sí puede ir midiendo la duración de
su viaje. El
otro "falso gemelo" no puede ir midiendo la
duración de ese viaje que él no realiza, aunque
cuando el viajero regrese ambos podrán cotejar sus
relojes y, entonces sí, comprobar que han transcurrido
tiempos diferentes para cada uno de ellos. |
|
|
| |
|
|
| |
Una vez se ha
comprendido este problema es conveniente concebir
otras situaciones en las que los hermanos puedan viajar
separadamente y lo hagan de tal modo que cuando se reencuentren
tengan la misma edad. Como es evidente, el requisito que se ha
de cumplir para que así ocurra es que los dos hermanos realicen
sendos viajes realmente idénticos respecto de algún sistema de
referencia, o, podríamos decir mejor,
que no se rompa la simetría de la situación con respecto a ambos
gemelos. |
|
| |
|
|
| |
|
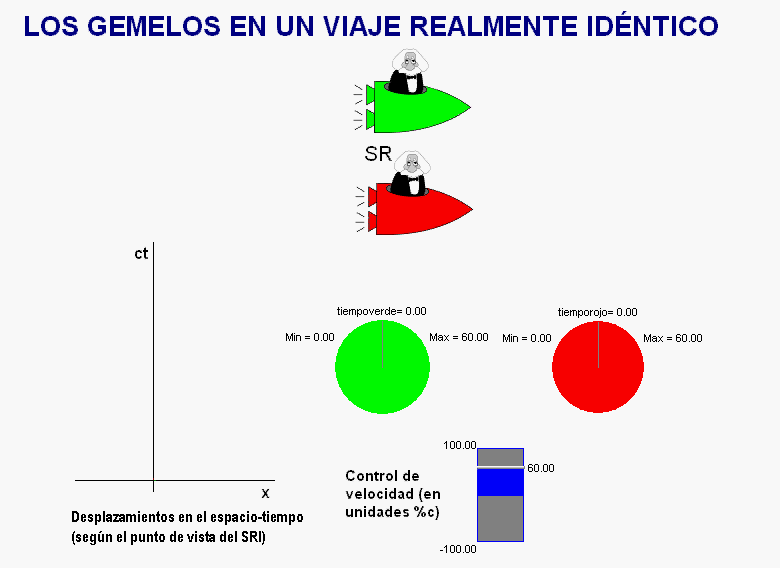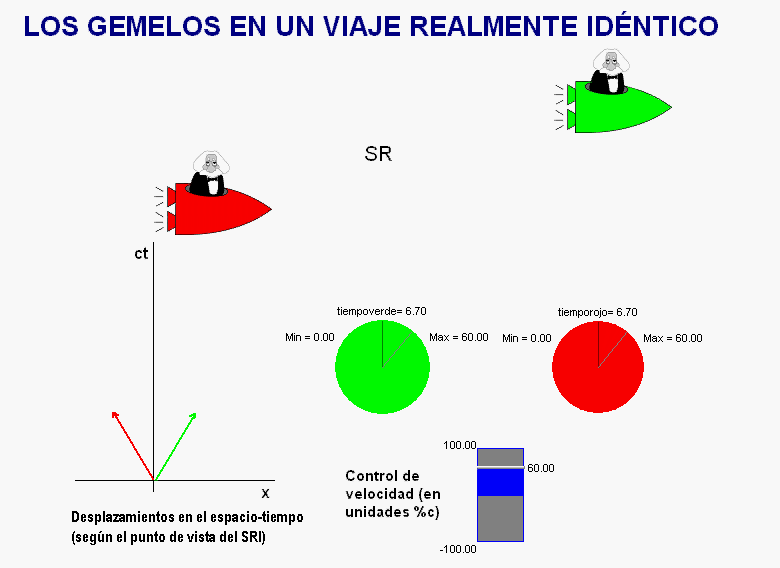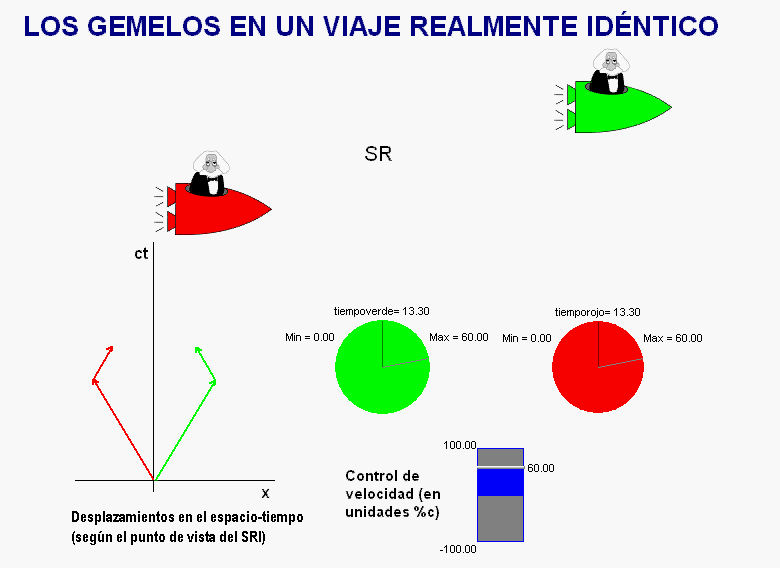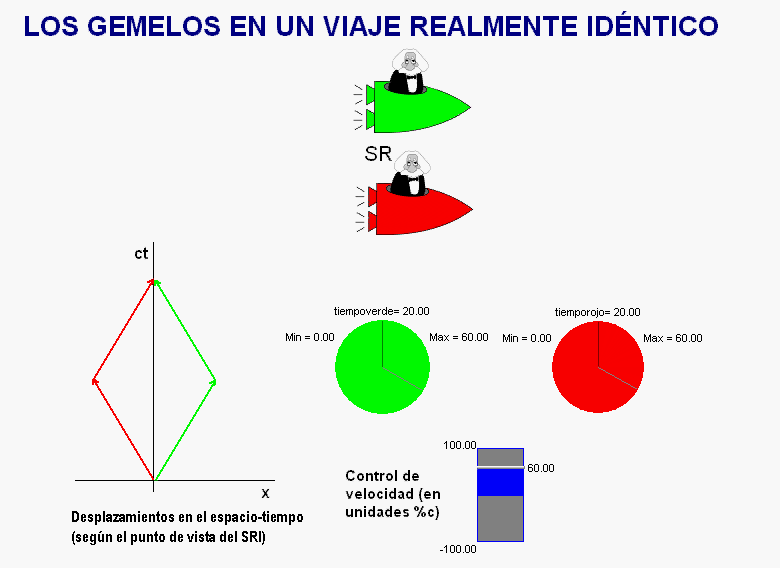
La
animación adjunta muestra una posible solución de este
tipo.
Como vemos, ahora los dos hermanos realizan sendos
viajes que resultan simétricos al ser representados en
un diagrama espacio-tiempo ligado a un sistema de
referencia exterior a ambos.
En estas condiciones, ambos
tienen la misma edad al reencontrarse.
Clic
aquí
para
descargar esta animación.
Para usarla en tu
ordenador, descarga
Modellus |
|
 |
|
|
| |
|
|
| |
| |
Índice |
 |
|
|
|
| |
|
|
|

