| |
|
 |
PRINCIPIO DE
EQUIVALENCIA |
 |
|
|
|
|
|
|
Reproducimos aquí algunos aspectos del razonamiento
original que permitió a Einstein avanzar hacia la
generalización de la relatividad. Lo sugirió en 1907,
volvió a él en 1911, y, a partir de entonces, lo utilizó
como un principio básico.
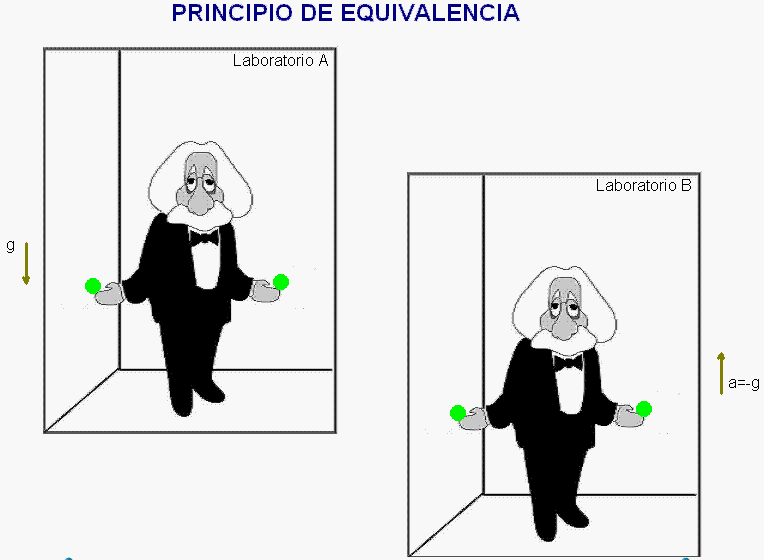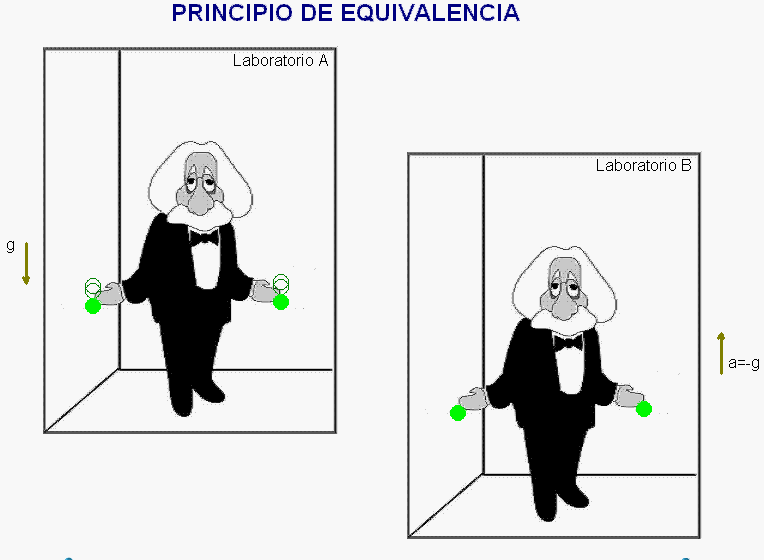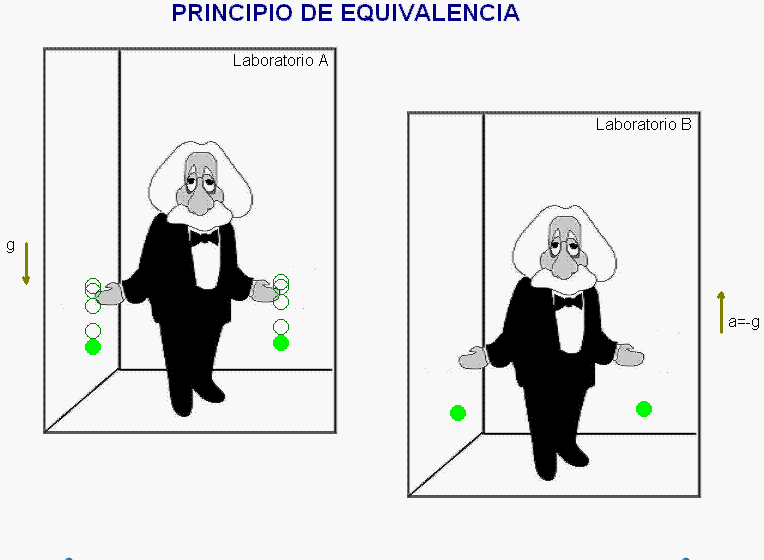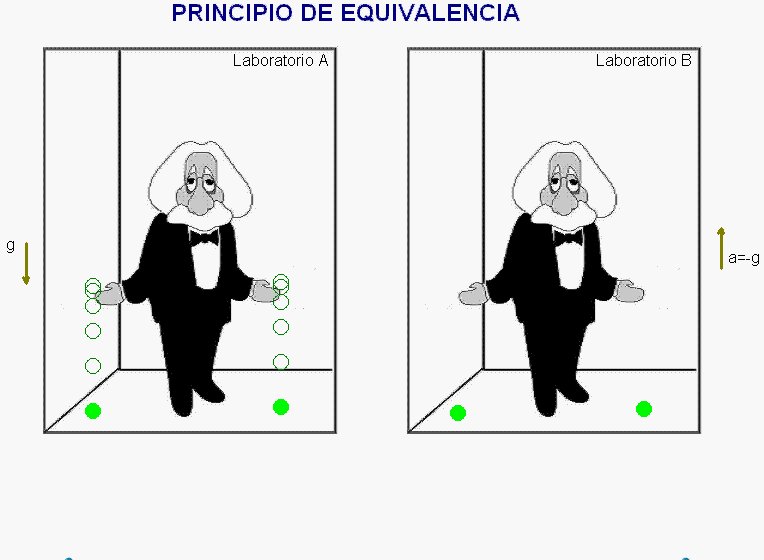
El razonamiento comienza considerando un laboratorio, A,
en reposo en un campo gravitatorio uniforme y otro
laboratorio ideal, B, supuestamente aislado y, en
consecuencia, no sometido a fuerzas gravitatorias. Se
pretende comparar el comportamiento mecánico de los
objetos en ambos laboratorios.
Como ejemplo de una
situación mecánica que permite realizar esta
comparación, se considera el movimiento de dos esferas
que se dejan libres en ellos.
La animación adjunta reproduce el resultado de este
experimento mental en
el laboratorio
A,
donde
las esferas sufren la acción del campo gravitatorio
uniforme de intensidad g.
Como
simula la animación,
debido a la
equivalencia
entre masa inercial
y masa gravitatoria,
las dos esferas caen
ahí
con
la
misma aceleración a = g
Clic
aquí
para
descargar esta animación.
Para usarla en tu ordenador instala
Modellus |
|
 |
|
|
|
|
Pensemos ahora en el
laboratorio ideal, B, no sometido a ningún campo
gravitatorio. En estas condiciones ideales ese
laboratorio es un sistema de referencia inercial (SRI). Por lo tanto, se le puede aplicar
el
primer postulado de la relatividad especial.
Esto significa que los objetos que se suelten ahí han de
compartir cualquier movimiento rectilíneo y uniforme que
el laboratorio pueda tener. Dicho de otro modo, mientras
el laboratorio ideal tenga un movimiento rectilíneo y
uniforme, las esferas permanecerán en reposo dentro de
él. |
|
|
|
Entonces, ¿cómo se puede conseguir
en ese laboratorio ideal que las dos esferas
tengan el mismo comportamiento mecánico que
tienen en el laboratorio terrestre?, es decir,
¿cómo se puede hacer que caigan en su interior
con una aceleración igual a g?
Sencillamente, pensó Einstein,
dotando al laboratorio ideal de esa misma
aceleración, a = g, pero dirigida en sendito
contrario ("hacia arriba").
La
animación adjunta muestra el resultado de este
experimento mental de Einstein en los dos laboratorios.
A los ojos del observador ubicado dentro de cada uno de
ellos, dicho resultado es idéntico, con lo que,
siguiendo este razonamiento, no podrá saber si su
laboratorio está sometido a un campo gravitatorio o si,
en ausencia de él, está acelerado.
Clic
aquí
para
descargar esta animación.
Para usarla en tu ordenador instala
Modellus
|
|
 |
|
|
|
|
La generalización de este
razonamiento conduce a una consecuencia muy importante
en relación con el problema de la relatividad: no se
puede distinguir por medio de experimentos mecánicos
un sistema de referencia sometido a un campo
gravitatorio uniforme de intensidad, g, de otro sistema
de referencia que, no sometido a ningún campo
gravitatorio, tenga una aceleración
constante, de sentido contrario e igual a g. Si esta conclusión fuera cierta, no
únicamente en relación con experimentos mecánicos, sino
para cualquier tipo de pruebas, resultaría que cualquier
aceleración constante se podría sustituir, a todos los
efectos, por un campo gravitatorio uniforme y viceversa. Einstein se dio cuenta de la importancia de esta
posibilidad y, en el camino hacia la construcción de la
teoría de la relatividad general, elevó esta hipótesis a
la categoría de principio fundamental. El resultado se
denomina principio de equivalencia y se puede expresar
así: |
|
|
|
Principio de
equivalencia: Sean dos sistemas de referencia: un
sistema de referencia K, no acelerado o inercial, en el
que actúa un campo gravitatorio uniforme; otro sistema
de referencia K’, que acelera uniformemente con respecto
a K, pero en el que no actúa campo gravitatorio alguno.
Estos dos sistemas de referencia son equivalentes, es
decir, los experimentos que se lleven a cabo bajo
condiciones idénticas en estos dos sistemas de
referencia darán lugar a resultados idénticos. |
|
|
|
El
principio de equivalencia relaciona la
aceleración uniforme con la gravedad uniforme. Ahora
bien, los campos gravitatorios reales producidos por los
objetos del cosmos (estrellas, planetas, galaxias, etc.), no son, ni mucho
menos, uniformes. Por ejemplo, el
campo gravitatorio
creado por la Tierra no tiene el mismo valor en todos
los puntos de su superficie, debido a la forma achatada
y densidad no uniforme de nuestro planeta. Además varía muy
apreciablemente con la distancia al centro del planeta y
sus líneas de fuerza no son paralelas, sino que forman
un haz dirigido hacia dicho centro de la Tierra. Además, cada punto de la superficie terrestre
no está fijo, sino animado de un movimiento de rotación.
Como consecuencia de todo esto, el campo gravitatorio
terrestre (e igualmente el creado por cualquier otro
objeto del Universo) no puede ser imitado simplemente
tomando un enorme laboratorio y acelerándolo. Sin
embargo, si se limita el procedimiento a pequeños
laboratorios sin rotación y durante pequeños intervalos
de tiempo, sí se puede reproducir
localmente dicho campo gravitatorio. Esto se hace tanto
mejor cuanto más pequeños sean los laboratorios y cuando
menor sea el intervalo de tiempo adoptado. Desde
un punto de vista formal esto
significa que, estrictamente, la
equivalencia en el mundo real entre un laboratorio
sometido al campo gravitatorio y otro laboratorio ideal
acelerado convenientemente, sólo se puede establecer a
nivel local, es decir, cuando se adopta un intervalo
infinitesimal del
espacio-tiempo. |
|
|
| |
|
|
| |
| |
Índice |
 |
|
|
|
| |
|
|
|