masa inercial y masa gravitatoria

EQUIVALENCIA ENTRE LA MASA INERCIAL Y LA MASA GRAVITATORIA

Consideramos dos cuerpos, de masas gravitatorias, m_1gy m_2g, colocados a una cierta altura del suelo terrestre. Suponemos que tienen una forma adecuada para minimizar el rozamiento con la atmósfera (se consigue una buena aproximación usando pequeñas esferas metálicas). Las esferas cuelgan de dos muelles idénticos, cuyos estiramientos delatan que la Tierra les ejerce una fuerza de atracción diferente. En estas condiciones, la intensidad de la fuerza de atracción de la Tierra sobre cada esfera se calcula con la ley de gravitación:

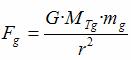Es decir, cuanto mayor sea la masa gravitatoria de la esfera, m_g , mayor es la fuerza de atracción que ejerce la Tierra sobre ella. Supongamos ahora que en un instante determinado se rompen los muelles y las esferas caen hacia la superficie de la Tierra. ¿Cómo cae cada una?. Para responder a esta cuestión calculamos la aceleración de los respectivos movimientos de caída recurriendo al segundo principio de la Dinámica de Newton, en el que la propiedad relevante es la masa inercial, m_i , de la bola. Es decir:

a = F_res/m_i

Como la única fuerza que actúa sobre cada esfera es la fuerza de atracción de la Tierra (F_res=F_g) se deduce la siguiente expresión para el módulo de la aceleración de caída de cada esfera metálica:

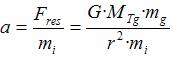En principio, esta aceleración de caída debería ser distinta para cada una de las esferas, dependiendo de los valores que tenga su masa inercial, m_i , y su masa gravitatoria, m_g. La esfera con masa gravitatoria mayor debería ser atraída más que otra de masa gravitatoria menor; pero, sometidas a la misma fuerza de atracción, la esfera de masa inercial mayor debería adquirir una aceleración menor que otra de masa inercial menor. Ahora bien, si la masa inercial y la masa gravitatoria fueran iguales (o proporcionales), m_i=m_g , sus efectos se compensarían y las dos esferas caerían con la misma aceleración. Esto es exactamente que ocurre y, por ello, decimos que la masa inercial y la masa gravitatoria son magnitudes equivalentes.

Podemos decir que la mecánica clásica intuyó la equivalencia entre la masa inercial y la masa gravitatoria, porque no diferenció estas dos magnitudes al concretar operativamente el segundo principio de la dinámica y la ley de gravitación universal. Al formular estas leyes (más concretamente al establecer las unidades de fuerza y de masa, así como el valor de la constante de gravitación universal, G) la mecánica clásica asignó la misma magnitud y la misma cantidad a la masa inercial y a la masa gravitatoria, lo que probablemente tuvo bastante que ver con el hecho de que entonces subyacía la idea de interpretar que toda masa (inercial o gravitatoria) debía indicar una misma cualidad de los objetos, ambiguamente entendida como su “cantidad de materia”.