| |
|
 |
EJERCICIOS DE DINÁMICA RELATIVISTA |
|
|
|
|
| |
|
| |
| ENUNCIAT |
Solució |
|
Una partícula choca cargada
contra otra de igual masa y el mismo tipo de
carga, inicialmente en reposo. Obtened el ángulo
que forman las trayectorias de salida de las
partículas aplicando: a) La Mecánica de Newton
(suponiendo que la colisión es elástica). b) La
Dinámica Relativista. |
 |
|
(5-2
p. 188)
En l’experiment pensat per Alväger i
col·laboradors s’observa la desintegració dels
mesons πo
neutres per a donar lloc a fotons d’alta
energia, γ.
Aquests mesons
πo
tenen energies entre 6,0 i els 18,0 GeV,
energies en repòs de 135,1 MeV i vides mitjnes
pròpies de 2·10-16 s.
(a) Quin
és l’interval de velocitats dels mesons
πo?
(b) Quin
és l’interval en què estaven compreses les vides
mitjanes en el sistema del laboratori?
(c) Quina
distància recorren abans de desintegrar-se?
La velocitat dels raigs gamma pugué
determinar-se creant els mesons
πo,
i en conseqüència els raigs gamma, en ràfegues i
mesurant a continuació el temps que invertien
els raigs gamma de cada ràfega a recórrer una
distància determinada en una certa direcció. Si
aquesta distància fou de 60 m en el sistema de
laboratori, quin seria aleshores el temps de vol
per als raigs gamma que es mouen a la velocitat
c?
|
 |
|
(6-1,
p. 229)
Suposem que un fotó té una energia de 200 MeV i
es desplaça en la direcció de l’eix x. Suposem
que un altre fotó té una energia de 100 MeV i la
direcció la del eix y. (a) Quina és l’energia
total d’aquest sistema?, (b) Quina és l’impuls
total? (c) Si una partícula aïllada tingués
aquesta energia i impuls totals, quina seria la
massa de la partícula? (d) En quina direcció es
mouria? (e) Amb quina velocitat? |
 |
|
(6-2,
p. 229)
En determinat sistema de referència s’observa
que una partícula té una energia total de 5 GeV
i un impuls de 3 GeV.
(a) Quina és l’energia d’aquesta partícula en un
sistema en el que l’impuls val 4 GeV?
(b)
Quina serà la massa de la partícula?
(c) Quina és la velocitat relativa dels dos sistemes
de referència? |
 |
|
(6-3,
p. 229) Una
partícula de massa m i energia cinètica
2mc2 xoca contra una altra
partícula en repòs la massa de la qual és 2m
i roman unida a ella. Calculeu la massa en repòs
M de la partícula composta. |
 |
|
(6-4,
p. 230)
(a) Un fotó d’energia Ef xoca
amb una partícula estacionària de massa m
i és absorbit. Quina és la velocitat de la
partícula composta que resulta?
(b) Una
partícula amb una massa m que es mou a
una velocitat de 4c/5 xoca amb una
partícula semblant que està en repòs i es forma
aleshores una partícula composta. Quina és la
massa de la partícula composta i quina és la
velocitat d’aquesta?
|
 |
|
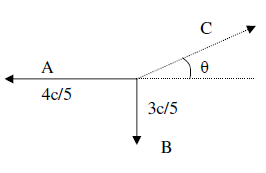
(6-5, p. 230) Una partícula de massa M es
troba en repòs en el laboratori quan es
desintegra en tres partícules iguals, cada una
de les quals té una massa m. Dues de les
partícules, A i B, tenen les velocitats i
direccions indicades en la figura.
(a) Calculeu la direcció i la velocitat de la partícula C.
(b)
Trobeu el quocient M/m. |
 |
|
 |
|
(6-7, p. 231) Un coet de fotons fa servir radiació
pura per a la propulsió. Si les masses inicial i
final del coet són Mi i Mf,
demostreu que la velocitat final V del coet
relativa al sistema de referència en repòs
inicial vé donat per l’equació adjunta |
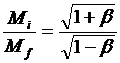 |
|
 |
|
(6-8,
p. 231) Una
nau espacial porta una mena de vela que rep
l’empeny d’un raig làser dirigit cap a ella des
de la Terra. Si la vela es perfectament
reflectora, calculeu la massa de la llum que cal
per accelerar un vehicle de massa M fins un
valor determinat de
g.
|
 |
|
(6-9,
p. 231) Un
làser amb una massa de 10 kg està situat en
l’espai lliure i apunta a la Terra. El làser
emet contínuament 1020 fotons/s amb
una longitud d’ona de 600 nm, mesurada en el
sistema propi. En t = 0 el làser es troba en
repòs respecte de la Terra.
(a) Inicialment, quanta energia radiant es
rep a la Terra en la unitat de temps?
(b) La radiació emesa cap a la Terra fa que
el làser s’allunye del nostre planeta. Quina
serà la velocitat del làser relativa a la Terra
després que hagen transcorregut 10 anys (temps
del làser)?
(c) En l’instant en què el làser es mou a una
velocitat
βc relativa a
la Terra, quant menor és la velocitat a la que
es rep l’energia en la Terra respecte a la
velocitat original quan β
= 0? Calculeu el valor per a t = 10 anys (temps
del làser).
(d) Indica la forma en què un observador
situat en la Terra pot explicar, aproximadament,
per què la velocitat de recepció disminueix
contínuament en funció de la conservació de
l’energia. |
 |
|
(6-10
p. 231)
Un àtom amb un estat excitat d’energia Qo
per sobre de l’estat fonamental es mou amb una
velocitat V cap a un comptador de
centelleig. L’àtom es desintegra i passa a
l’estat fonamental d’aquest mitjançant l’emissió
d’un fotó d’energia Ef, com
indica el comptador, assolint d’aquesta manera
el repòs. Si la massa de l’àtom és m, demostreu
que: |
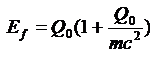 |
|
 |
|
(6-11,
p. 232) El
messó neutre
po
es descompon en dos raigs
g,
i no res més. Si un
po,
la massa del qual és de 135 MeV, es mou amb una
energia cinètica d’1 GeV:
(a) Quines són les energies dels raigs
g
si el procés de desintegració fa que siguen
emesos en sentit oposat segons la trajectòria
original del
po?
(b) Quin angle formen els raigs
g
si són emesos formant un angle igual respecte de
la direcció del moviment del
po? |
 |
|
(6-12,
p. 232) Un
antiprotó
p- amb
una energia cinètica de 2/3 GeV xoca contra un
protó p que es troba en repòs al
laboratori. S’anihilen mitjançant la reacció
p+ +p->
γ1
+ γ2, és a dir, es creen dos
fotons gamma que marxen en sentit directe o
invers segons la línia que recorre l’antiprotó
en incidir. La massa del protó i antiprotó
suposem que és d’1 GeV cada una.
(a) Quines són les energies que tenen els
fotons?
(b) En quina direcció marxen cadascun
dels fotons?
(c)
Quina energia té cada un dels
fotons mesurada en el sistema de referència fix
a l’antiprotó
p- incident? |
 |
|
(6-13,
p. 232) Un
positró amb una energia cinètica de 0,51 MeV
xoca inelàsticament amb un electró en repòs i es
crea un àtom de positroni que retrocedeix
lliurement. L’electró i el positró que formen el
positroni s’anihilen en vol creant dos fotons
g.
(a) Quina és la velocitat de l’àtom de
positroni?
(b)
Quina és l’energia màxima possible per a
un dels fotons produïts mitjançant aquest procés
d’anihilació? |
 |
|
(6-14
p. 232)
Demostreu que els processos que s’indiquen a
continuació són impossibles des del punt de
vista dinàmic:
(a) Un
fotó xoca amb un electró en repòs i transfereix
tota l’energia a l’electró.
(b) Un
fotó situat en l’espai lliure es transforma en
un electró i un positró.
(c) Un
positró i un electró en repòs es destrueixen
s’anihilen creen un únic fotó. |
 |
|
(6-15,
p. 232-3)
(a) Si un protó amb una energia cinètica de 437
MeV xoca inelàsticament amb un protó en repòs i
els dos protons reboten amb energies iguals,
quin és l’angle existent entre tots dos? (b) Si
el protó que entra té una energia total de 33
GeV, quin s l’angle que formen tots dos protons
resultants?
|
 |
|
(6-16
p. 233)
La teoria usual de l’efecte Compton considera el
cas d’un electró lliure en repòs que es abastat
per un fotó que es dispersat en un fotó
d’energia menor. Suposem que un fotó d’energia
Ef, xoca amb un electró en moviment de massa m,
com indica la figura. Quina velocitat inicial
tindrà l’electró si, com a conseqüència del xoc,
el fotó retrocedeix amb la mateixa energia Ef
que el fotó incident?
|
 |
|
(6-18
p. 233)
(a) Un fotó d’energia hυ
xoca
elàsticament amb un electró en repòs. L’energia
del fotó després del xoc és de hυ/2
i marxa formant un angle de 60o amb
la direcció original. Quin és el valor de
υ?
Quin tipus de fotó n’és?
(b) Un fotó amb una energia hυ xoca amb un àtom
excitat que es troba en repòs. Després del xoc
el fotó continua tenint una energia hυ,
però el sentit del moviment experimenta un canvi
de 180o. Si l’àtom es troba en
l’estat fonamental després del xoc, quina és
l’energia d’excitació inicial?
|
 |
|
(6-19
p. 233)
Un fotó d’energia gran xoca i és dispersat per
un protó que es troba inicialment en repòs i pot
retrocedir lliurement. El protó retrocedeix
formant un angle de 30o amb una
energia cinètica de 100 MeV.
(a) Quina
era l’energia del fotó incident?
(b) Quina
és la direcció i l’energia del fotó dispersat? |
 |
|
(7-1,
p. 260) La
massa del messó K és mKc2
= 494 MeV i la del messó
p,
mpc2
= 137 MeV. Un messó K que recorre el laboratori
es descompon en duos messons
p.
Un messó roman en repòs.
(a) Quina és l’energia de K?
(b)
Quina era l’energia de l’altre messó
p?
|
 |
|
(7-2
p. 260)
Un raig gamma,
γ, abasta un electró en repòs i crea una parella electró positró:
γ
+ e- e- +
e+ + e-
Quina serà l’energia mínima del raig
γ que ha fet possible aquest procés?
|
 |
|
(7-3,
p. 261)
Suposem que un accelerador pot subministrar als
protons una energia cinètica de 200 GeV. La
massa del protó, m, és 0,938 GeV.
Calculeu la màxima massa possible, M,
d’una partícula X que pot produir-se per la
col·lisió d’un d’aquests protons d’elevada
energia amb un protó en repòs segons el procés
següent:
p
+ p p + p + X |
 |
|
(7-6
p. 261)
L’energia cinètica Ec d’un sistema en
coordenades de laboratori età relacionada amb
l’energia Ec* en el
sistema del centre de masses en el cas no
relativista mitjançant l’expressió Ec=Ec*+MV2/2,
a on M és la massa total del sistema i V la
velocitat del centre de masses. Quina és
l’expressió anàloga per al cas relativista?
Demostreu que es redueix al cas anterior si
totes les velocitats són molt menors que c.
|
 |
|
 (7-7,
p. 261) Un
fotó d’energia E marxa cap a l’origen
O d’un sistema de coordenades K
formant un angle
α amb l’eix y,
com s’indica a la figura. Fent ús de les
transformades de Lorentz Einstein per a
l’energia i l’impuls calculeu l’energia del
fotó, E’, en un sistema K’ en el
qual s’observa que el fotó recorre cap avall
l’eix y’. (7-7,
p. 261) Un
fotó d’energia E marxa cap a l’origen
O d’un sistema de coordenades K
formant un angle
α amb l’eix y,
com s’indica a la figura. Fent ús de les
transformades de Lorentz Einstein per a
l’energia i l’impuls calculeu l’energia del
fotó, E’, en un sistema K’ en el
qual s’observa que el fotó recorre cap avall
l’eix y’.
|
 |
|
(7-9
p. 262)
El ciclotró és una màquina emprada per accelerar
els ions positius a energies d’uns pocs MeV
(veure figura). Les D són cuirasses metàl·liques
que fan pantalla als camps elèctric, però no els
magnètics. Existeix, per tant, un camp magnètic
efectiu B en tot l’interior del recipient
metàl·lic en el que s’ha fet el buit i un camp
elèctric altern, sinusoïdal, en la petita
obertura entre les D. Quan aquest camp es troba
en fase amb els ions, aquests reben un impuls
cada semicercle. Aquests impulsos augmenten
l’energia i, per tant, el radi de l’òrbita dels
ions fins que, finalment, són expulsats per la
finestra.
(a) Quina
és la freqüència a la qual els ions
recorren el ciclotró? Demostreu que la
resposta és independent de l’energia
cinètica dels ions si v<<c. Obteniu el
resultat numèric corresponent al cas
dels protons si suposem que B = 1,5 T.
(b) Si el màxim diàmetre
que pot utilitzar-se en l’interior de
les D és 60 cm, quines són l’energia
cinètica màxima i la velocitat màxima
que poden assolit el protó?
(c)
Si
els protons reben un impuls de 105
volt cada vegada que travessen la separació
entre les dues D, quantes revolucions efectuaran
abans d’escapar per la finestra Quant de temps
dura el procés sencer?
(c) Quina
dificultat tècnica sorgeix si el màxim diàmetre
que es pot fer servir augmenta fins a 6 m, per
exemple?
|
 |
| |
Radi de curvatura =
34,0 cm
|
|
(7-10
p. 262)
En un experiment amb una cambra de boira [H.
Whiteside, J. N. Palmieri i R. A. Burnstein,
Am. J. Phys., 34, 1005 (1966)],
s’observà que un mesó K-
interaccionava amb un protó en repòs i
s’obtenia, en conseqüència, un mesó
π+ i una partícula
desconeguda, X, i s’hi obtenien les tres
trajectòries que es mostren a la figura. El camp
magnètic en l’interior de la cambra de boira era
de 1.7 (+-0.7) T.
(a) Per
què les trajectòries que tenen com origen el
vèrtex O, punt d’intersecció, indiquen que el K-
es trobava en repòs en l’instant de la
intersecció?
(b) Identifiqueu la partícula desconeguda fent ús de
la taula que es dóna a continuació. |
|
 |
|
|
|
Nom |
Símbol |
|
|
|
Positró, electró |
e+, e- |
0,511 |
+1, -1 |
|
Muó |
μ+,
μ- |
105,7 |
+1, -1 |
|
Mesó pi |
π+,
π- |
139,6 |
+1, -1 |
|
Mesó K |
K+, K- |
493,8 |
+1, -1 |
|
Protó |
p+ |
938,3 |
+1 |
|
Neutró |
n |
939,6 |
0 |
|
Lambda |
Λo |
1.115,4 |
0 |
|
Sigma més |
Σ+ |
1.189,4 |
+1 |
|
Sigma zero |
Σo |
1.192,3 |
0 |
|
Sigma menys |
Σ- |
1.197,2 |
-1 |
|
Xi zero |
Ξo |
1.314,4 |
0 |
|
Xi menys |
Ξ-1 |
1.320,8 |
-1 |
|
Omega menys |
Ω- |
1.675 |
-1 |
|
 |
|
|
|
|
Los enunciados de todos los problemas, excepto el
primero de esta lista, proceden del libro de
A.P. French, Relatividad especial (Reverté;
Barcelona) |
|
|
|
|