PROBLEMAS DE FÍSICA DE MATERIALES Y DE FÍSICA BIOMÉDICA EN BACHILLERATO

Tema

Artículos

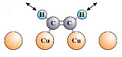
(*) Vibraciones moleculares: Las energías de vibración de las moléculas son discretas, como ocurre con los niveles energéticos de los electrones en un átomo. En este problema, se utiliza el principio de la conservación de la energía para hallar el potencial necesario para excitar las moléculas en función de su frecuencia de vibración y, con ese resultado, a partir de los espectros vibracionales obtenidos en un Microscopio de Efecto Túnel, se identifican dos moléculas con átomos ligeros de masas distintas, aproximando sus modos de vibración al Movimiento Armónico Simple.

Single-Molecule Vibrational Spectroscopy and Microscopy (C.B Stipe, M.A. Rezaei y W. Ho; Science,) (1998)

Nanoscale Science of Single Molecules using Local Probes (J.K. Gimzewski y Ch. Joaquin, Science) (1999)

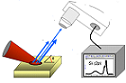
(*) Efecto fotoeléctrico: En este problema se profundiza sobre los niveles electrónicos correspondientes a los iones de un metal y se ve una ampliación sencilla de la ley simplificada del efecto fotoeléctrico. A partir de los espectros de fotoemisión de electrones, se identifican los niveles electrónicos profundos de un material metálico y se calcula la energía cinética de los electrones que provienen de dichos niveles.

Spectroscopic evidence for Ag (III) in Highly Oxidized Silver Films by X-ray Photoelectron Spectroscopy (T.C. Kaspar, T. Droubay,  S.A. Chambers y P. S. Bagus; J. Phys. Chem. C.) (2010)

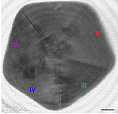
(*) Difracción de electrones: La difracción de electrones se utiliza de forma muy habitual en física de materiales para identificar y analizar la estructura cristalina de los sólidos. En este ejercicio se obtiene el ángulo respecto al haz incidente, de los electrones que dan lugar al primer máximo y se deduce el número total de máximos de interferencia. Para resolverlo se usa la ley de De Broglie, la relación no relativista entre energía y momento, y la condición de la interferencia constructiva.

Ambient-stable tetragonal phase in silver nanostructures (Y. Sun, Y. Ren, Y. Liu,  J. Wen,  J.S. Okasinski y D.J. Miller; Nature) (2012)

(*) Laser: En este problema se calcula la dispersión natural de frecuencias de la luz de un láser de HeNe, se evalúa en qué grado es monocromática,  se deduce la expresión general de la longitud de onda de la luz emitida por la cavidad en función de la longitud de dicha cavidad óptica, y se ve cómo generalizar esa expresión cuando el medio activo es un sólido (p.ej. un nanohilo). Para su resolución se usa el principio de incertidumbre de Heisenberg y las leyes sobre ondas estacionarias.

Lasing in robust cesium lead halide perovskite nanowires (Eaton S et al, Nat. Acad. Sci. 113) (2016)

Single-nanowire electrically driven lasers (Duan et al. Nature) (2003)

Efecto Hall: El efecto Hall se produce cuando se ejerce un campo magnético transversal sobre un conductor por el que circulan cargas. Como la fuerza magnética ejercida sobre ellas es perpendicular al campo magnético y a su velocidad (ley de la fuerza de Lorentz), las cargas son impulsadas hacia un lado del conductor y se genera en él un voltaje transversal o voltaje Hall. En Física de Materiales, la medida del efecto Hall se puede utilizar para medir la densidad de portadores en un material y así, en el primer problema (*) se recrean datos de una investigación reciente referida al estudio del óxido de estroncio y titanio (STO). En biomedicina del efecto Hall se aplica a determinar la velocidad de circulación del flujo sanguíneo, así como la concentración de los iones en la sangre, como muestra el segundo problema (**).

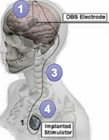
(**) Propiedades físicas de las neuronas: Las neuronas tienen unas propiedades eléctricas diferentes a las del resto de células del cuerpo humano, siendo así las únicas capaces de generar y transmitir el impulso nervioso. En este problema se aplican leyes básicas de la electrostática y de la electrodinámica para obtener propiedades eléctricas pasivas de una neurona (resistencia, capacitancia,..) y, también, para determinar magnitudes necesarias para su estimulación artificial, como la densidad de carga que ha de atravesarla y la densidad mínima de corriente que han de aportar los electrodos para lograr esa estimulación.

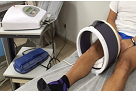
(**) Fuerza de Lorentz: Una aplicación actual del uso de campos magnéticos en medicina es conseguir una aceleración del metabolismo en la recuperación de ciertas lesiones, pues las moléculas que intervienen en las reacciones metabólicas son iones disueltos que hay en nuestro organismo. En este problema, se usa la ley de la fuerza de Lorentz para calcular la frecuencia que ha de tener un campo magnético para estimular el metabolismo de varios tipos de tejido.

(**) Ecografía Doppler: Este tipo de ecografía utiliza ultrasonidos y permite visualizar las ondas de velocidad del flujo que circula por vasos sanguíneos. En el problema se aplica la ley del efecto Doppler para obtener la resolución mínima en frecuencias que debe tener el dispositivo, usando datos plausibles y a partir de la imagen obtenida en una prueba real.

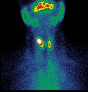
(**) Desintegración radiactiva: En un problema se aplica la ley de desintegración radiactiva a la técnica de la gammagrafía, calculando la dosis de material radiactivo que hay que inyectar a un paciente. En otro, se aplica la misma ley a la técnica de datación de un resto orgánico encontrado en un yacimiento

Technetium in nuclear medicine (AG Jones - Radiochimica Acta) (1995),