| |
|
 |
LEYES DE LA DINÁMICA
RELATIVISTA |
 |
|
|
|
|
|
|
Ya se ha visto que
el módulo del
cuadrivector espacio-tiempo
es una magnitud invariante y que,
como el cuadrivector impulso-energía, P, es proporcional a
él, su módulo (definido de
forma análoga) también es una magnitud invariante.
Expresado en unidades de energía el
cuadrado de dicho módulo es: |
|
|
|
P2
=
E2 –
(p·c)2 |
|
|
|
|
En particular,
en el sistema de referencia ligado a la partícula
(sistema de referencia propio), se tiene que el factor
gamma es igual a la unidad y que la velocidad de la
partícula es cero. Entonces, en este referencial,
resulta P2 = (mc2)2.
Pero, como esta magnitud es invariante, este valor de
P2 es el mismo en cualquier sistema de
referencia inercial y, por tanto, se puede escribir la
siguiente ecuación general que relaciona la masa, el
impulso y la energía: |
|
|
|
(m·c2)2 =
E2 – (p·c)2 |
|
|
|
A esta ecuación que relaciona las tres magnitudes
dinámicas, la podemos considerar como ley fundamental de la
dinámica relativista, ya que relaciona entre sí a las
tres magnitudes básicas en dinámica (masa, impulso y
energía) y de ella se pueden deducir varias expresiones
particulares de interés. |
|
|
|
Conviene
señalar, por otra parte, que la proporcionalidad entre
el cuadrivector cinemático espacio-tiempo y el
cuadrivector dinámico impulso-energía implica que
los cocientes entre sus componentes
respectivas sean
iguales
(considerando sólo una componente espacial, se tiene:
dx/cdt = px·c/E).
Entonces, como el módulo de la
velocidad de la
partícula es v = dx/dt, se
cumple la siguiente relación entre
la
velocidad, v,
y las magnitudes dinámicas
(impulso, p, y energía, E): |
|
|
|
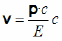 |
|
|
|
La tabla adjunta
recoge todas las expresiones ya obtenidas y otras
expresiones particulares que que es importante
considerar en dinámica relativista (aplicables a una
partícula de masa, m).
Todas ellas se deducen de forma bastante sencilla a
partir de ecuación fundamental de la dinámica
relativista (deducciones en
este documento).
En los siguientes
apartados se comentan aspectos conceptuales relativos a
dos de estas expresiones particulares que no se han comentado todavía: la
equivalencia entre masa y energía, y la relación entre
la energía y el impulso de la luz.
|
|
|
Magnitudes de la dinámica
relativista |
|
Cuadri-vector impulso-energía |
P
= (E,
p·c)
|
|
Impulso
lineal |
p
= m·γ·v |
|
Energía |
E = m·γ·c2 |
|
Relación
entre
el
cuadrado del módulo de P y la masa,
m
(en unidades de energía) |
P2 = (mc2)2
|
|
Ley fundamental de la dinámica relativista
|
(mc2)2 = E2 – (p·c)2
|
|
Relación entre la velocidad, la energía y el
impulso lineal. |
v =[(p·c)/E]·c |
|
Equivalencia entre la masa y la energía (propia) |
Eo = m·c2 |
|
Energía cinética |
Ec = E-Eo |
|
Relación entre la energía y el impulso lineal de
entidades físicas de masa nula
(fotones) |
E = p·c |
|
Expresiones aplicables a una
partícula de masa (invariante) m |
|
|
|
|
|
| |
|
|
| |
| |
Índice |
 |
|
|
|
| |
|
|
|
|
|
|