| |
|
 |
REPRESENTACIÓN DE SUCESOS E HISTORIAS EN EL ESPACIO-TIEMPO |
 |
|
|
| |
|
|
| |
|
|
|
Un
suceso es
un hecho puntual que ocurre en un cierto lugar y un
cierto instante, sin que llegue a transcurrir tiempo.
En
cinemática se determina dando en un sistema
de referencia inercial cuatro valores: las coordenadas
espaciales (x, y, z), que proporcionan su posición, y la
coordenada temporal, t.
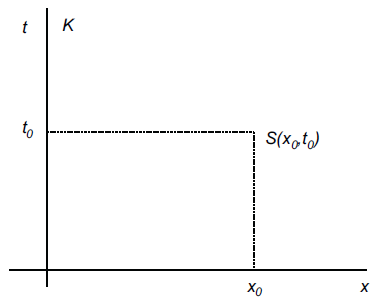
Así, el modo de
representar un suceso S de coordenadas (x0,
y0, z0, t0)
es construir un diagrama espacio-tiempo, en el que, para hacer la representación más
sencilla, se reduce el análisis de las cuatro a
dos dimensiones: una coordenada
espacial, x, y la coordenada temporal, t.
Las
representaciones abstractas de sucesos y de procesos físicos sobre
dos ejes (x, t) son similares a las gráficas del movimiento
que se utilizan ordinariamente para describir
movimientos en la
mecánica de Newton, salvo una diferencia ya vista al definir el
cuadrivector espacio-tiempo: En relatividad se
suele representar el tiempo en el eje vertical
(ordenadas) y la posición en el eje horizontal (abcisas). |
|
 |
|
|
|
|
Al exigir el
cumplimiento de los postulados de la relatividad
especial, los diagramas espacio-tiempo adquieren un
perfil particular y proporcionan unas conclusiones
coherentes con esta teoría y completamente diferenciadas
de las predicciones de la mecánica de Newton. |
|
|
|
 |
|
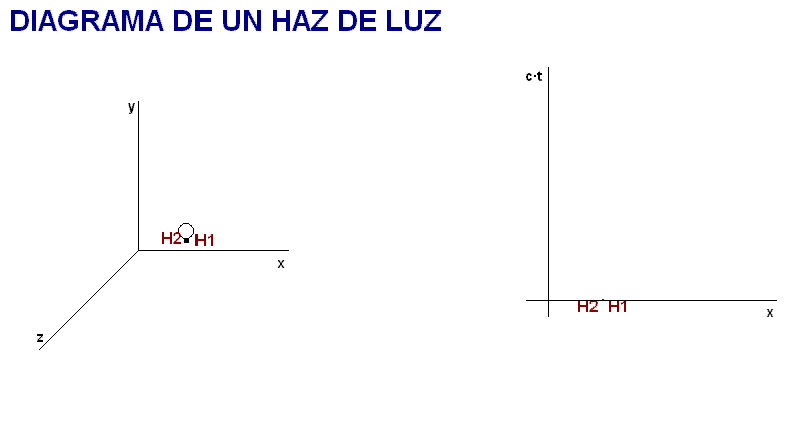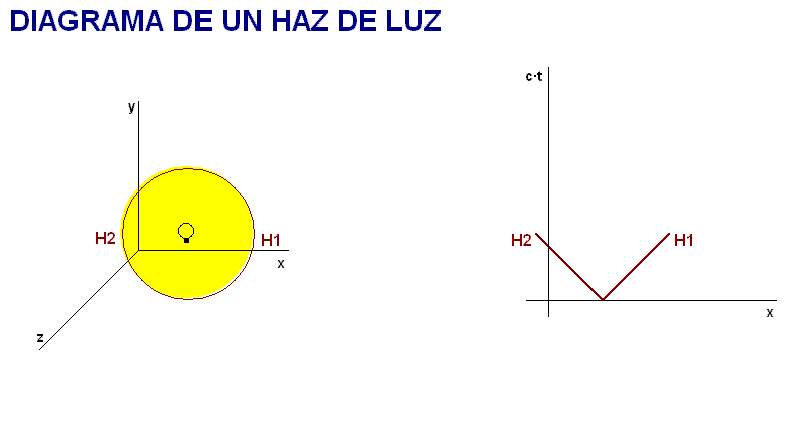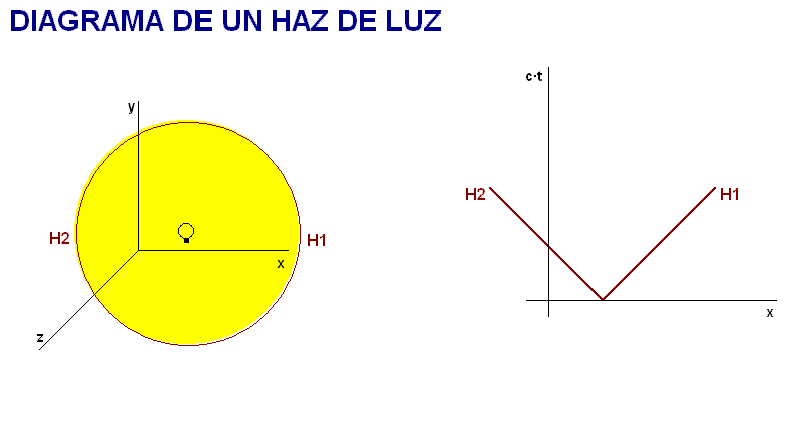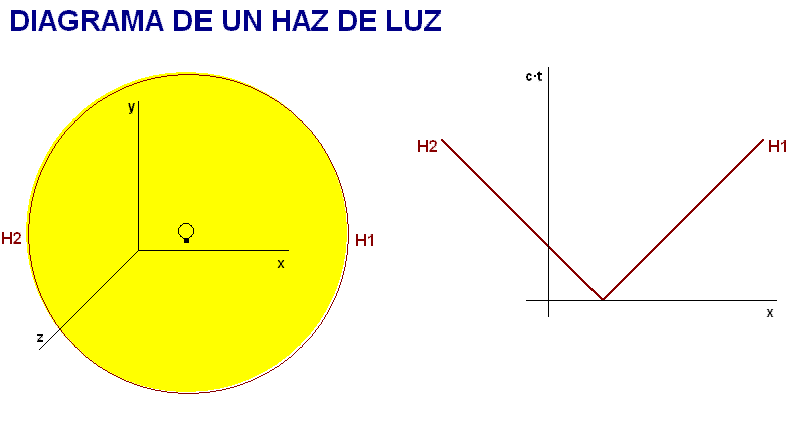
Para empezar a verlo, se puede considerar la
representación de una haz de luz emitido por una
bombilla con respecto a un determinado SRI.
De acuerdo con las predicciones
relativistas la onda electromagnética
correspondiente a ese haz luminoso se propaga en
todas las direcciones a la velocidad c, y la representación de la historia del haz
en el diagrama ha
de reflejar el avance de dos extremos del mismo,
H1 y H2, a la velocidad, c,
respectivamente en el sentido positivo y en el sentido
negativo del eje X.
Por tanto, graduando el eje de
tiempos como c·t (ya se ha dicho que esto se hace con objeto de usar
la dimensión espacial y una misma unidad en
todos los ejes), la evolución de los extremos
del haz de luz se representa en el diagrama como
muestra la animación adjunta (a la izquierda
de este texto)
Clic
aquí
para
descargar esta animación.
Para usarla en tu
ordenador, descarga
Modellus
|
|
|
|
|
Esta representación tiene más importancia de la
que pueda parecer a primera vista, debido a que c, además de ser la velocidad de la
luz, es el límite superior de velocidad,
que ningún objeto material puede alcanzar. |
|
|
|
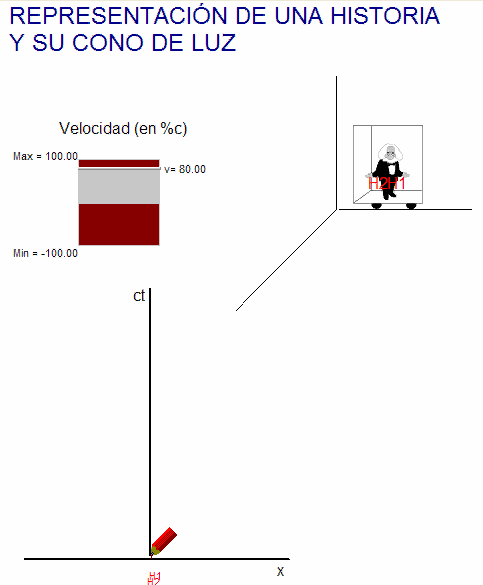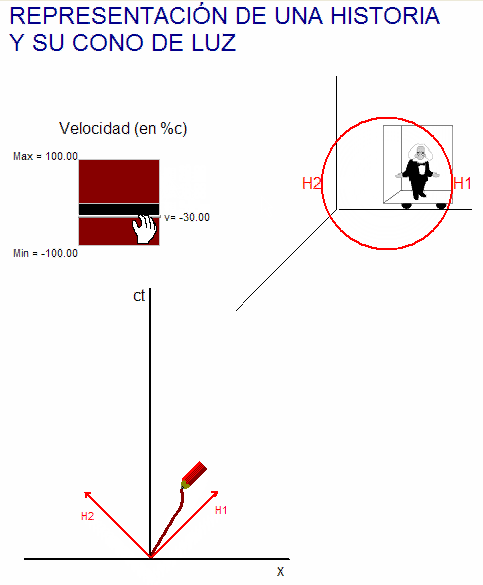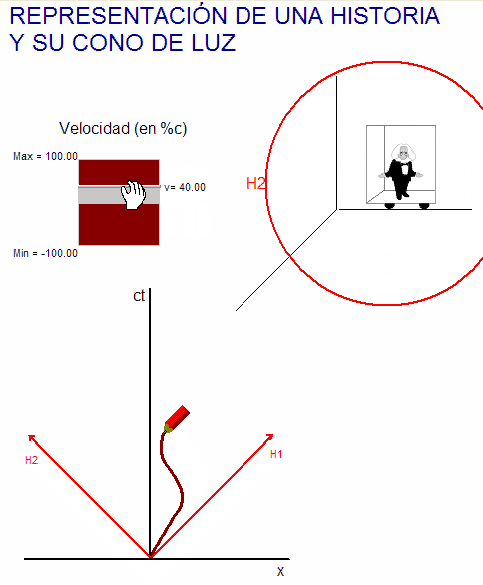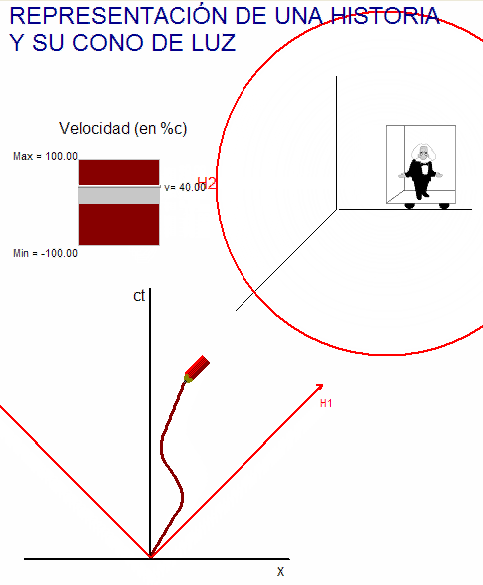
Por tanto, cuando
se traza la
curva representativa de otro movimiento cualquiera que
también comience ahí (podría ser, por ejemplo, el de una persona que en ese lugar encendió la
lámpara) se ha de tener en cuenta que dicha curva se
tiene que ubicar en el interior de la zona que delimitan
las historias de las puntas H1 y H2 del haz de luz pues
su velocidad siempre es inferior a la velocidad límite
c.
Además, su pendiente, respecto del eje vertical de
tiempos, ha de tener en todos los puntos un valor
inferior a las pendientes de las rectas OH1 y OH2.
Para practicar este concepto se puede usar
la animación adjunta, en la que el usuario puede mover a nuestro "Einstein"
viajero y comprobar que la representación de su viaje
queda necesariamente dentro del "cono de luz". Entrando en la
ventana del modelo físico-matemático de la animación
se constata que este comportamiento es consecuencia
de la existencia del límite superior de velocidades, c.
Clic
aquí
para
descargar esta animación.
Para usarla en tu
ordenador, descarga
Modellus
El matemático
Herman Minkowski
(1864-1909), antes profesor de Einstein y luego
admirador de su obra,
fue
quien primero planteó estos
diagramas y mostró sus potentes aplicaciones.
Diagramas espacio-tiempo
de Minkowski |
|
 |
|
|
|
| |
|
|
| |
| |
Índice |
 |
|
|
|
| |
|
|
|
|
|
|
|