| |
|
 |
CURVATURA DEL
ESPACIO-TIEMPO |
 |
|
|
|
|
|
|
Aunque
en una proporción muy pequeña en relación a su
tamaño, el Universo esta poblado por materia, que
se localiza en objetos, como estrellas,
planetas, granos de polvo, etc., y en
agrupaciones de estos, como galaxias.
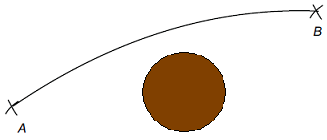
La
presencia de estos cuerpos celestes y/o
agrupaciones de materia provoca la
deflexión de la
luz, es decir, hace
que los rayos lumínicos no sigan trayectorias
rectilíneas, sino que se desvíen o se curven, y
lo hagan tanto más cuanto más cerca pasen esos rayos de
cada agrupación de materia y/o cuanto mayor sea la
masa de ésta. |
|
 |
|
|
|
|
Estas trayectorias curvas que describe la luz en el
Universo se llaman líneas geodésicas y, puesto que la
luz viaja por ellas a la
velocidad límite, señalan la distancia más corta entre sus
extremos. Desde un punto de vista geométrico este hecho
revela que el espacio-tiempo es curvo y que, por
este motivo, en él se ha de aplicar una geometría no
euclidiana, que es diferente a la geometría más tradicional
a la que estamos acostumbrados. |
|
|
|
 |
|
Un ejemplo sencillo de geometría no euclidiana
se tiene analizando lo que ocurre en una
superficie esférica. Pensemos en una esfera que
tenga trazados meridianos como si fuera un globo
terráqueo (figura adjunta). Estos meridianos las líneas geodésicas de la superficie esférica y se
corresponden con las líneas rectas paralelas de
la geometría tradicional euclidiana.
Sin
embargo, a diferencia de lo que ocurriría sobre
una superficie plana bidimensional donde sí es
aplicable dicha geometría euclidiana, en la superficie
esférica la distancia entre dos meridianos no es
constante, sino que éstos se aproximan cada vez
más al acercarnos a los polos de la esfera y se
separan al alejarnos de ellos.
|
|
|
|
|
Igualmente
tampoco se cumplen en la superficie esférica curva otras leyes de la
geometría tradicional euclidiana:
La distancia más corta entre dos puntos, en
lugar de seguir una línea recta, sigue una línea geodésica; la
suma de los tres ángulos de un triángulo no es
igual sino mayor que 180º; el teorema de Pitágoras de
los triángulos rectángulos deja de cumplirse, etc. |
|
|
|
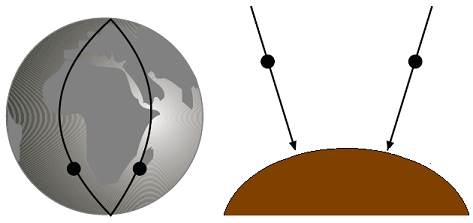
Para completar la analogía entre la superficie
esférica y el espacio-tiempo curvado, se puede
imaginar a dos cuerpos "abandonados" en el
Universo en un lugar próximo a un objeto celeste
y compararlos con otros dos cuerpos que se
desplacen libremente por dos meridianos de la
superficie esférica.
Los dos cuerpos del mundo real caen libremente en el
campo gravitatorio creado por el objeto celeste,
y, por ello, sus trayectorias se aproximan entre sí cada vez más. Del mismo modo, los dos cuerpos que
viajan libremente por los meridianos de la
superficie esférica también se aproximan entre
sí cada vez más al irse acercando al polo de la
esfera. |
|
 |
|
|
|
|
Así pues,
en el marco de la relatividad general se establece esta
profunda relación entre la geometría del espacio-tiempo
y el campo gravitatorio existente en el Universo: Dicho
campo gravitatorio produce la curvatura del
espacio-tiempo. |
|
|
|
|
|
|
|
Estos hechos están en la base de la relación que se
establece
entre la teoría de la relatividad general y la de relatividad especial.
Del mismo modo que
la teoría de la relatividad especial marca unos límites
a la aplicabilidad de la mecánica de Newton, la teoría
de la relatividad general señala otros a la
aplicabilidad de la relatividad especial. De este modo,
la relatividad general incluye a la relatividad especial
como caso extremo, de forma que las leyes y
expresiones de la primera devienen hacia las
de la segunda cuando
la influencia de las masas tiende a cero, lo que, como
acabamos de ver, ocurre en
las zonas del espacio-tiempo suficientemente alejadas de
esas masas. En estas regiones el entramado
espacio-tiempo casi es plano y la aplicación de las
leyes de la relatividad
especial proporciona unos resultados que apenas se
desvían de los que proporciona la aplicación de las
leyes de la relatividad general.
En cambio, al aproximarnos a cualquier objeto celeste,
es imprescindible utilizar la teoría de la relatividad general. |
|
|
|
Para terminar este apartado, diremos que, en consonancia
con estos conceptos, las
ecuaciones fundamentales de la relatividad general
relacionan de forma cuantitativa la intensidad del campo
gravitatorio con la materia. Dichas ecuaciones toman la
forma general: |
|
|
|
R = G·M |
|
|
|
Donde R es un objeto matemático (formalmente es un
tensor) que representa a la curvatura del
espacio-tiempo, M es otro objeto matemático que
representa a la materia presente y G representa a la
constante de gravitación universal. En cada caso
particular, las posibles soluciones que pueden
proporcionar estas ecuaciones generales dependen de las
acotaciones que se hagan a la región de Universo en la
que se aplican, de la cantidad y la distribución de masa
que se considere o que se conozca en esa región, etc. |
|
|
 |
|
"Einstein tenía razón". Artículo del Dr.
D. Rafael Bachiller García, director del
Observatorio Astronómico Nacional, sobre
la confirmación experimental de las distorsiones
del espacio-tiempo usando la sonda espacial de
la NASA Gravity Probe B (publicado en 2008 en la
serie "Cronicas del Cosmos" por el mundo.es) |
|
|
|
| |
|
|
| |
| |
Índice |
 |
|
|
|
| |
|
|
|