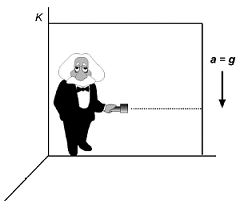
Para hacerlo, podemos considerar una pequeña región del espacio afectada por un campo gravitatorio uniforme y "vertical" (como, podría ser, por ejemplo, una zona de dimensiones reducidas en las proximidades de la superficie de la Tierra). Imaginamos que alguien enciende en ese lugar una linterna, la cual envía un rayo luminoso en dirección horizontal. La pregunta es: ¿Qué trayectoria tiene la luz ahí? Para responderla, hay que adoptar un sistema de referencia, K, que caiga libremente en ese lugar con una aceleración a=g. De acuerdo con el principio de equivalencia, este sistema de referencia acelerado es locamente equivalente a un sistema de referencia inercial (SRI) y en él se aplica la relatividad especial, según la cual la luz tiene ahí tiene un movimiento rectilíneo, horizontal y uniforme a la velocidad c (figura adjunta). Entonces, como el sistema de referencia, K, está cayendo, se deduce que con respecto a otro referencial ligado al suelo (sometido al campo gravitatorio), el rayo de luz ha de tener una trayectoria curva.