DIAGRAMAS MÚLTIPLES

 
     
 

 

Después de haber dibujado los ejes (x, ct) del diagrama espacio-tiempo, según el punto de vista de un sistema de referencia inercial, K, se pueden incorporar en el mismo dibujo los ejes (x', ct') de cualquier otro sistema de referencia inercial, K', que se desplace con una velocidad v respecto de K.

Como el mostrado en la figura adjunta situada  a la izquierda, en el que se ha considerado que para el instante inicial  de ambos SRI (t  = t´ = 0), las posiciones de sus orígenes coinciden (x = x´ = 0)
 
 
 

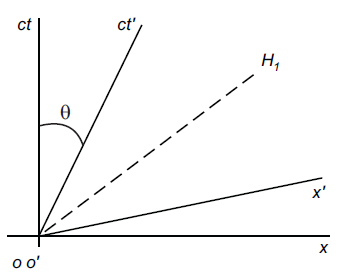
Para construir ese diagrama doble, se tiene en cuenta, en primer lugar, que la historia del origen O' del SRI K' es (según el punto de vista del sistema de referencia inercial K) el eje de tiempos ct'. Ello es así porque dicho origen O' está, para todo tiempo t', en la posición x' = 0.

Una vez dibujado ese eje temporal ct', se utiliza el hecho de que la luz tiene la misma velocidad, c, en ambos sistemas de referencia para añadir al diagrama el eje espacial x'. Un haz de luz que se emita desde el origen común justamente en el instante t = t' = 0 en el que coinciden ambos orígenes, x = x '= 0, tiene la velocidad, c, en los dos referenciales. Por tanto, el eje espacial x' ha de ser simétrico al eje temporal ct', para que el extremo del haz de luz, H1, sea la bisectriz del diagrama respecto de los ejes de ambos sistemas de referencia inerciales.

Quedando, por tanto, dibujado finalmente el diagrama doble (que da los puntos de vista de los dos SRI, K y K') tal como se muestra en la figura adjunta, situada a la derecha.

  

 
     
 

Utilizando este procedimiento se pueden incorporar cuantos sistemas de referencia inerciales se desee al diagrama. El eje temporal de un sistema de referencia inercial que avance en sentido positivo del eje x del sistema de referencia inercial K se inclina hacia la derecha del dibujo en esta representación abstracta (tiene una inclinación mayor o menor, respecto del eje temporal c·t del sistema de referencia inercial K) según sea mayor o menor la velocidad de dicho sistema de referencia respecto de K). Para otro sistema de referencia inercial que avance en sentido negativo del eje x del sistema de referencia inercial K, su eje temporal se inclina hacia la izquierda del dibujo.

  
     
 

 

La animación adjunta enseña el procedimiento para la construcción de diagramas múltiples.

Clic aquí para descargar esta animación. Para usarla en tu ordenador, descarga Modellus

Para profundizar en la construcción de diagramas múltiples de Minkowski, se puede consultar este documento.
 
 
 
 
 

Índice