| |
|
 |
PRECESIÓN DE LOS
PERIHELIOS |
 |
|
|
|
|
|
|
Las teorías anteriores a la relatividad general no
pueden hacer predicciones totalmente correctas sobre los
procesos físicos porque no tienen en cuenta la
influencia de la
materia sobre el entramado espacio-tiempo en el
que dichos procesos ocurren. Concretamente, las
predicciones acerca del movimiento de cualquier objeto
del Universo, sea utilizando la mecánica de Newton o sea
utilizando la propia teoría de la relatividad especial,
producen resultados que se desvían de los hechos
empíricos. |
|
|
|
 |
|
El ejemplo más notable de esta desviación de
los hechos empíricos sobre el movimiento de
objetos celestes respecto de las predicciones de
la mecánica de Newton, que resolvió la
relatividad general, se refiere a los
movimientos de los planetas en sus órbitas
elípticas alrededor del Sol.
La teoría
newtoniana predice un movimiento adicional para
el planeta, si añadimos a la interacción del Sol
sobre el planeta la atracción gravitatoria de
otros objetos (por ejemplo, otros planetas del
Sistema Solar) y tenemos en cuenta además que la
inclinación de la eclíptica influye en la
percepción de la trayectoria descrita por el
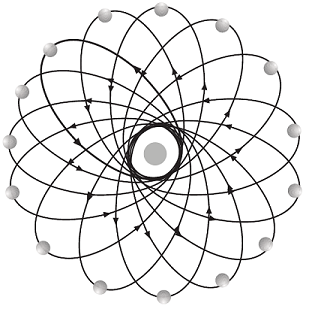
planeta desde la Tierra. Este movimiento adicional se puede
describir diciendo que los perihelios de dichas
elipses han de realizar una trayectoria de
precesión (figura adjunta).
Ahora bien, resulta
que la precesión observada de los perihelios de
los planetas no se corresponde estrictamente con
la predicha al aplicar la mecánica de Newton.
Sobre todo, en algunos casos. El más evidente es
el del planeta Mercurio para el que se detecta
experimentalmente una precesión residual que no
se puede explicar aplicando la mecánica de Newton. En cambio, una
aplicación rigurosa de la teoría de la
relatividad general sí explica satisfactoriamente
esta precisión residual. |
|
|
|
|
En efecto,
de acuerdo con la relatividad general, la precesión en
radianes por revolución que se añadiría al movimiento de
precesión de los perihelios planetarios, se calcula
utilizando la expresión siguiente: |
|
|
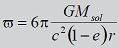 |
|
|
|
En esta expresión Msol es la masa del
Sol, r es el semieje mayor de la órbita del planeta, e
es la excentricidad de la órbita y G·Msol/c2 es
una cantidad, que es igual para todos los planetas y recibe el
nombre de radio gravitacional del Sol. De acuerdo con esta expresión, la precesión es
tanto mayor cuanto más cerca del Sol está el planeta (r
menor) y cuanto mayor es su excentricidad (e mayor). En
el caso de Mercurio, que hace una revolución cada 88
días, al sustituir los valores (G = 6,67·10-11 N·m2/kg2,
MSol = 1,989·1030 kg,
c = 3·108 m/s, e = 0,2056,
r = 5,834·1010 m)
se obtiene una precesión residual de 42.9" cada siglo. |
|
|
|
Como este valor de la
precesión residual
es muy pequeño, para poder analizar la concordancia de los
datos experimentales con esta
predicción de la relatividad general, fue necesario
recoger medidas ópticas durante bastantes años, con objeto de que el efecto
acumulado fuera observable. Sin embargo, esta situación
cambió con el descubrimiento en el año 1975 por parte de Hulse y Taylor de un púlsar en un sistema binario.
Como se comenta en
este apartado del tema dedicado al campo gravitatorio,
este
sistema está constituido por dos estrellas muy compactas
y densas que orbitan una alrededor de la otra a una
velocidad elevada (del orden de 10-3 c), describen una
trayectoria de excentricidad también elevada (e es
0.617) y producen un campo gravitatorio muy intenso
(G·M/c2 del orden de 10-6). En consecuencia, el
periastro debería tener una velocidad de precesión del
orden de 4.2º al año. Este valor es suficiente para que
sea relativamente accesible su observación precisa y, de
hecho, todos los datos que se han obtenido de la
observación de este sistema binario se han mostrado
consistentes con la relatividad general. |
|
|
| |
|
|
| |
| |
Índice |
 |
|
|
|
| |
|
|
|