La dilatación temporal de origen gravitatorio se puede deducir en términos cualitativos aplicando el principio de equivalencia. Para hacerlo, empezamos por imaginar una situación en la que hay sendos relojes idénticos en un punto A, situado en la superficie de la Tierra, y en otro punto B, situado a una considerable altura de dicha superficie. Imaginamos también que en cada uno de esos lugares (A y B) hay una fuente luminosa que emite un destello de luz cada tic-tac del reloj colocado ahí y que esos destellos emitidos en A y en B, viajan hacia el otro lugar (B o A).

Es ahora cuando usamos el principio de equivalencia, en virtud del cual consideramos en los lugares A y B, sendos sistemas de referencia (SR) ideales equivalentes a los laboratorios reales sobre los que se ejerce la acción del campo gravitatorio de la Tierra. Estos sistemas de referencia no están sometidos a ningún campo gravitatorio, sino que tienen una aceleración ascendente e igual al valor de la gravedad en cada lugar (a=-g). Ahora bien, como el campo gravitatorio se orienta en el sentido de B hacia A, el SR adoptado en B se acelera, alejándose de los destellos de luz que proceden de A. Por ello, esos destellos procedentes de A llegan a B a un ritmo más lento que el tic-tac del reloj situado en B. De donde se deduce que, según el punto de vista de observador situado en B, el reloj de la Tierra, A, marcha más lento que el suyo (B).

¿Qué conclusión se obtiene analizando el comportamiento de los destellos que se emiten en B según el punto de vista de un observador situado en A? La misma, puesto que, según este punto de vista, los destellos procedentes de B se dirigen a un SRI equivalente en el suelo (A) que se aproxima hacia ellos cada vez más deprisa. Por lo tanto, A también deduce que el reloj situado en B marcha más deprisa que el suyo (A).

En resumen, con ambos puntos de vista se obtiene la misma conclusión, de que el tiempo transcurre más lentamente en el lugar donde la gravedad es mayor (A) y más rápidamente en lugar donde la gravedad es menor (B).

Para poner en evidencia la dilatación temporal de origen gravitatorio, Einstein imaginó átomos incandescentes como relojes, cuyos ritmos son determinados por la frecuencia de la luz que emiten. Esto le permitió extraer una conclusión acerca de dicha frecuencia y de la correspondiente longitud de onda.

En efecto, para aplicar las conclusiones que se acaban de obtener sobre la dilatación temporal de origen gravitatorio al caso particular de posibles relojes atómicos, podemos suponer que cada tic-tac de uno de estos relojes corresponde a una oscilación de la onda lumínica o del pulso de luz que dichos relojes emiten o absorben cuando ocurre en ellos una transición entre dos de sus niveles atómicos. 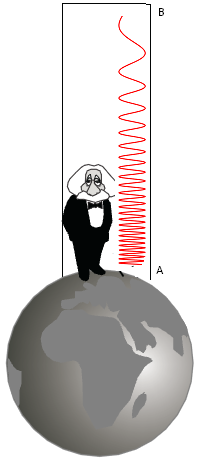Ahora bien, para que tenga lugar la dilatación temporal gravitatoria cada pulso recibido (cada tic-tac) en un lugar elevado, B, donde el campo gravitatorio es más débil, tiene que corresponder a varios tic-tac  (varios pulsos) del reloj atómico que lo emitió en un punto de la superficie de la Tierra, A, donde el campo gravitatorio es más intenso. Tal como se indica el dibujo adjunto, esto implica que la luz procedente de átomos situados en el suelo terrestre A  se reciba en un punto situado a una altura elevada, B, con longitud de onda mayor (menor frecuencia).

Una luz visible de frecuencia más baja es una luz de longitud de onda mayor y, por lo tanto, desplazada hacia el color rojo del espectro. Por eso, a este hecho se le denomina desplazamiento gravitacional hacia el rojo (esta expresión se ha de entender como un desplazamiento del espectro completo, ya que, obviamente, se aplica a todas las radiaciones, tanto visibles como invisibles). Como se acaba de ver, el desplazamiento hacia el rojo se debe a lo que les sucede a las señales luminosas cuando atraviesan el espacio-tiempo en presencia de la gravedad. Podemos interpretar que ésta hace perder energía a los fotones cuando ascienden en sentido opuesto a la orientación del campo gravitatorio.