| |
|
 |
CARÁCTER RESTRINGIDO DE
LA RELATIVIDAD ESPECIAL |
 |
|
|
|
|
|
|
En
el tema dedicado a
la relatividad especial,
hemos visto que esta teoría
proporcionó un avance impresionante
a la ciencia porque consiguió establecer una
equivalencia
entre los
sistemas de referencia inerciales
(SRI)
para el estudio de las leyes
que rigen todos los procesos físicos. Por primera vez en la historia de la física se
dio una respuesta
explícita al
problema
de la relatividad de los movimientos.
Esta respuesta
se formalizó
operativamente a través de unas nuevas
leyes de
transformación
de las magnitudes al pasar de un SRI. Utilizando estas
leyes
de transformación,
las leyes fundamentales del
electromagnetismo
y
las de la mecánica relativista se escriben igual en
todos los SRI. En
consecuencia, en cualquier SRI se pueden aplicar ambas
teorías para
estudiar cada proceso físico. |
|
|
|
Después de apreciar esta gran aportación de la teoría de
la relatividad
especial resulta casi inevitable plantear una seria
objeción a
la misma. Paradójicamente esta objeción está relacionada
con el
reto fundamental
de la relatividad, es decir, con el reto de extender la
aplicabilidad de
todas las leyes de la física a todos los sistemas de
referencia. Porque,
efectivamente, la relatividad especial
consiguió que
todas
las leyes físicas se puedan aplicar en los SRI
(los
mismos sistemas de referencia
en los que ya se podían aplicar las leyes de la
mecánica
de Newton).
Pero, ¿qué ocurre en sistemas de referencia que no sean
inerciales,
sino acelerados?
Por otro lado, ¿existe en el Universo algún SRI? |
|
|
|
Cuando se
analizan
las experiencias que tenemos a diario
en
vehículos acelerados, se
observa
que en
ellos
es posible efectuar pruebas que pongan de relieve su
aceleración. Por ejemplo,
un pasajero de un
autobús
nota la fuerza que
le hace el suelo mientras el
vehículo
arranca, cuando frena
o al trazar una
curva. Además, puede diseñar experimentos
calcular
la
aceleración
del autobús en el que viaja. Así, por ejemplo,
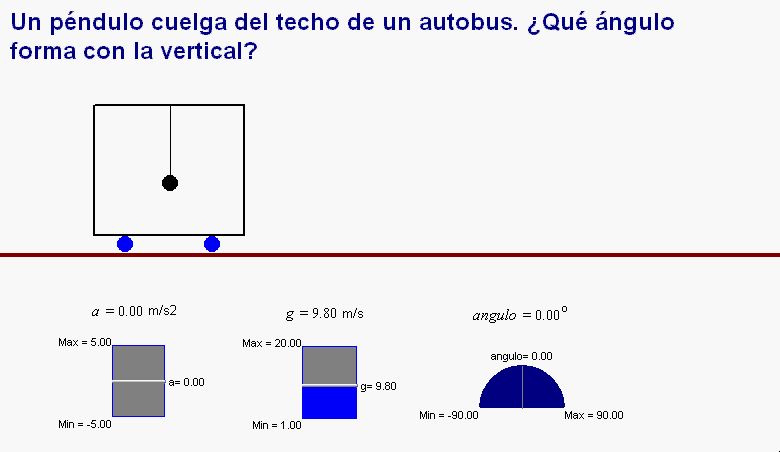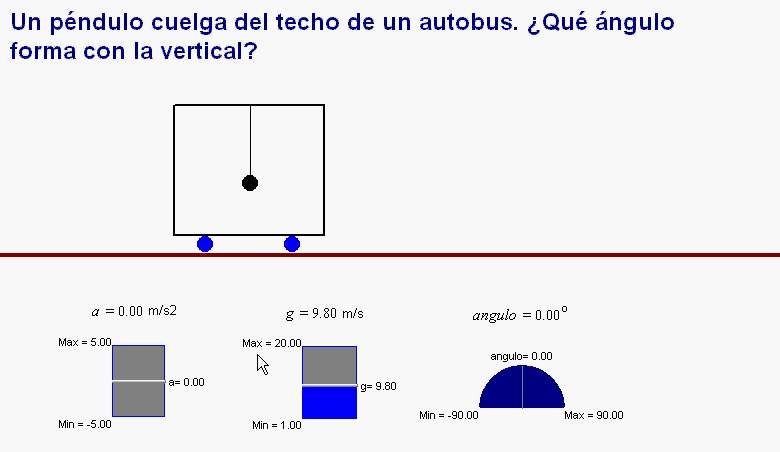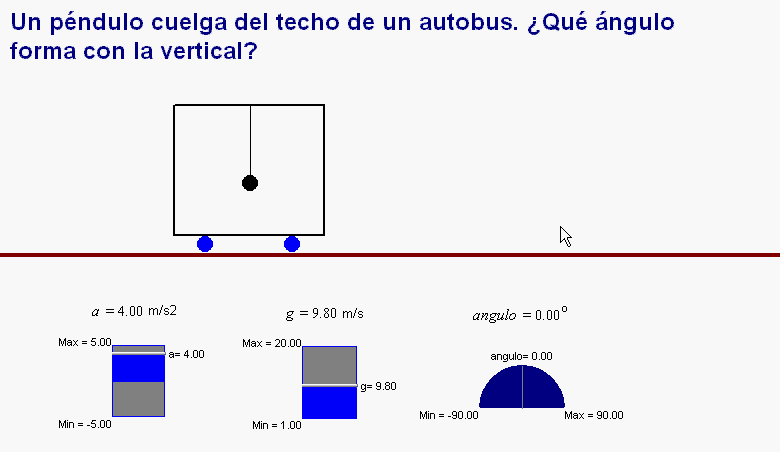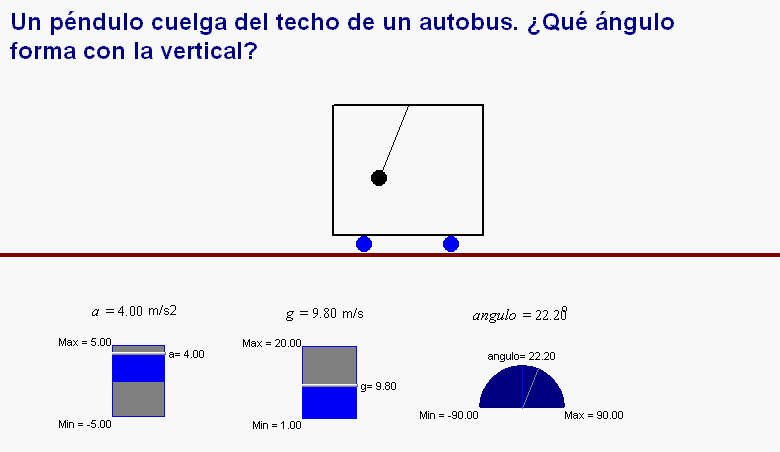
según muestra la animación adjunta (debajo), puede
colgar un péndulo
del techo.
Mientras el autobús mantenga un movimiento rectilíneo y
uniforme el péndulo se mantiene en posición vertical,
pero si el autobús acelera, el péndulo se desvía y el
viajero, después de medir el ángulo de dicha desviación,
puede calcular
la aceleración del
vehículo
(con
respecto
al suelo)
utilizando las
leyes de la mecánica
de Newton.
|
|
|
|
|
|
|
|
|
Así resulta que los
sistemas de referencia no inerciales (como el
ligado al tren acelerado) son perfectamente
identificables, distinguibles de los inerciales y, por
lo tanto, del reposo. Como consecuencia de ello, dichos
sistemas de referencia acelerados no cumplen el
primer
postulado de la relatividad especial, sino que,
en el marco de esta teoría, las leyes de la física no se
mantienen igual al trasladarlas a este tipo de sistemas
de referencia.
Este hecho no resulta nada satisfactorio para una mentalidad relativista. Con esta mentalidad inquieta
que dentro de un vehículo que cambia su velocidad, por
ejemplo de 5 km/s a 7 km/s, no se puedan detectar ni los
5 km/s ni los 7 km/s y sí, en cambio, el incremento de 2
km/s cada segundo. Dicho de otro modo, resulta
insatisfactorio que algo
tan fundamental como el principio de relatividad parezca
que sólo se pueda aplicar a un tipo de movimiento, el
movimiento uniforme. ¿No sería más lógico y deseable plantear que
todos los movimientos deberían ser, o bien absolutos, o
bien relativos? |
|
|
|
Estas inquietudes inducen
hacia un replanteamiento
del reto relativista, con el objetivo de extender la
aplicabilidad del principio de relatividad a cualquier
sistema de referencia en lugar de que la teoría quede
restringida a los SRI. Con más razón, si tenemos en
cuenta que cualquier sistema de referencia que se adopte en el Universo se ha
de ligar a algún objeto del cosmos, y, por tanto, será
acelerado, ya que todos los cuerpos celestes tienen movimientos acelerados
debido a que se ejercen entre sí fuerzas
gravitatorias. |
|
|
| |
|
|
|
