DOS EJEMPLOS DE APLICACIÓN DE LA DESCRIPCIÓN CUÁNTICA DE LA LUZ: REFLEXIÓN ESPECULAR E INTERFERENCIAS

 

Vamos a terminar este tema, mostrando dos ejemplos en los que resulta bastante sencillo justificar de manera cualitativa en el contexto de la física cuántica el comportamiento de la luz

 
 

El primero de los dos ejemplos será sobre la reflexión especular de la luz. Para desarrollarlo, consideraremos, tal como muestra la mitad de la figura adjunta situada más arriba (a), a una fuente emisora (representada por una bombilla) cuyas frecuencias supondremos que están en un intervalo muy pequeño alrededor de un valor central. Supondremos que la luz emitida por dicha fuente se propaga en el vacío, que incide sobre un espejo plano y luego parte de ella alcanza un detector (representado por un ojo).  Hemos colocado una pantalla opaca entre fuente y detector para indicar expresamente que la luz que llega a éste (al ojo) procede sólo del espejo

Como la luz es emitida por la fuente en todas las direcciones, al detector le puede llegar reflejada desde cualquier punto del espejo. En la mitad superior de la figura (a) hemos representado varios de esos caminos posibles de la luz entre la fuente y el detector (aunque, para tener mayor sencillez, sólo hemos dibujado caminos radiales, ya sabemos que se pueden tener caminos de cualquier tipo). Evidentemente, el tiempo de recorrido desde la fuente al detector es diferente para cada camino y mínimo para uno de ellos (el resaltado de color azul). En la mitad inferior de figura (b), se representa el tiempo recorrido por la luz desde la fuente hasta el detector para esos diferentes caminos, constatando que, efectivamente, el camino resaltado de color azul es el camino que cumple el principio de Feynman, es decir, es el que sigue la trayectoria de tiempo mínimo. Esa trayectoria es la misma que prevé la ley ordinaria de la reflexión, ya ese camino es el único que cumple que el ángulo de incidencia es igual al ángulo de reflexión.

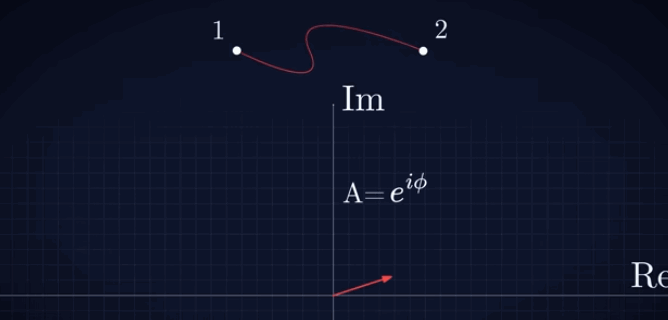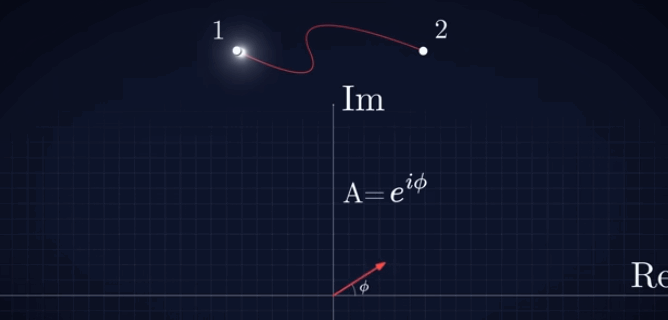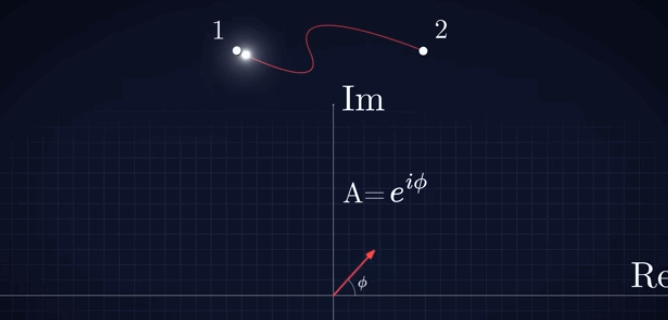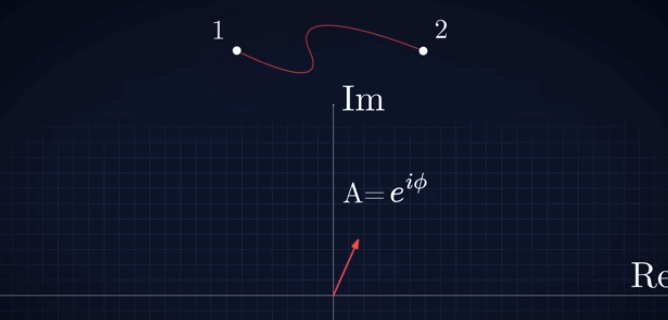
Dicho todo esto, para argumentar, en el marco de la teoría cuántica, que este camino es el camino preferente de la luz, procede aplicar el concepto expuesto en el apartado anterior de que en cada instante, la amplitud de probabilidad de encontrar al fotón en cualquier punto (en este caso, en el punto en que está el detector) ha de ser igual a la suma de las amplitudes de probabilidad en ese punto correspondientes a los diferentes caminos.

 

Como la fase de cada amplitud de probabilidad depende del tiempo de recorrido desde la fuente, en el detector es obvio que se tiene una fase diferente para cada camino. Estas fases determinan las interferencias, es decir, si las amplitudes de los diferentes caminos se cancelan o se realzan entre sí (equivalente a decir que la suma de los vectores que representan a las amplitudes da un vector de menor o mayor módulo).

 

Un análisis detallado muestra entonces que las amplitudes correspondientes a los caminos que están a la izquierda no inmediata del de tiempo mínimo (e igualmente las de los que están a la derecha no inmediata) se cancelan entre sí (interfieren destructivamente) en el detector, debido a la rápida variación de la fase, asociada a la rápida variación del tiempo de un camino a otro [como se aprecia cualitativamente en la figura anterior del problema situada debajo (b)]. Por tanto, al sumar esas amplitudes se obtiene una amplitud resultante prácticamente nula (equivalente a una interferencia destructiva), tal como muestra la figura (c) adjunta.

En cambio, los tiempos de recorrido para los caminos que están próximos al de tiempo mínimo son casi iguales entre sí, porque, como muestra igualmente la figura anterior (b), sus fases son muy similares, y ello da lugar a una amplitud resultante no nula (interferencia constructiva) en el detector, tal como muestra la figura (d).

  

 

 

En consecuencia, se concluye que la amplitud de probabilidad en el detector es, efectivamente, la que corresponde al camino de tiempo mínimo (que incluye los caminos vecinos inmediatos), corroborando la predicción, tanto del principio de Fermat, como de la ley ordinaria de la reflexión. Lógicamente, para cada posición del detector se tiene un camino de tiempo mínimo diferente, con un punto de incidencia distinto sobre el espejo.

 

Para complementar el ejemplo mostrado, termina este apartado y el tema entero con un breve apunte acerca de cómo se puede explicar de manera igualmente cualitativa el experimento de la doble rendija. Por sencillez, conviene, en este caso, suponer una fuente puntual de luz, equidistante de ambas rendijas (también supuestas puntuales), y cuyas frecuencias estén en un intervalo muy pequeño alrededor de un valor central. Bajo estas condiciones, en cada punto de la pantalla se obtiene la suma de dos amplitudes de probabilidad correspondientes a los dos caminos de tiempo mínimo que pueden considerarse desde la fuente hasta ese punto de la pantalla, pasando por las rendijas. Cuando esos tiempos sean tales que los vectores correspondientes a las amplitudes tengan la misma dirección y sentido, el módulo del vector suma tendrá el mayor valor posible, la densidad de probabilidad será máxima y se tendrá un máximo de luz. Esto es evidente que ocurre en el punto central de la pantalla, porque es equidistante de ambas rendijas. Por tanto, ahí se ha de obtener un máximo de intensidad lumínica. En cambio, cuando los tiempos de ambos caminos sean tales que los vectores tengan la misma dirección y sentido contrario, se tendrá un mínimo de luz. Lo que nos permite entender que, considerando todas las situaciones intermedias, quede descrita la figura de interferencia.
 
 
 
 
 

Índice