| |
|
 |
EL PRINCIPIO DE COMPLEMENTARIEDAD |
 |
|
|
|
|
|
|
Una
característica importante de la presunta "dualidad onda-corpúsculo"
fue su
sometimiento al denominado principio de complementariedad,
cuya formulación original se debe a
Bohr (1885-1962), quien
resaltó el hecho de que el observador interactúa con el
sistema en tal medida que condiciona la prevalencia de
uno u otro comportamiento (corpuscular u ondulatorio).
Literalmente expresó:
"Si se realiza un experimento para medir propiedades
ondulatorias de una partícula o de un fotón, se eliminan
peculiaridades corpusculares (y viceversa) y, de hecho,
ningún experimento puede mostrar a una partícula o a un
fotón manifestando simultáneamente ambos
comportamientos". |
|
|
|
Como es
lógico, esta
influencia del observador (del dispositivo experimental)
en el resultado del experimento fue objeto de candente
controversia y, a la vez, una fuente inspiradora de
fructífera investigación. Entre los experimentos más
destacados que
tuvieron una relación directa con esta controversia,
podemos mencionar, en primer lugar, uno realizado en 2007
en el CNRS (Centro Nacional para la Investigación
Científica en Francia). |
|
|
|
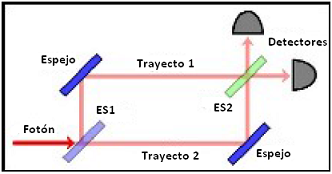
En dicho experimento, un emisor de fotones los enviaba de uno en uno
hacia un interferómetro y allí, cuando un fotón
pasaba por el primer espejo semi-reflectante (ES1), tenía la misma
probabilidad para seguir por dos trayectos
distintos (de 48 metros de longitud, cada uno),
que terminaban en sendos detectores. Justo antes
de esos detectores, se podía insertar o retirar
un segundo espejo semi-reflectante (ES2),
mediante un sistema sincronizado con el emisor
de fotones. Cuando se insertaba ese espejo, los
fotones podían alcanzar uno u otro detector, sin
ser "observados" y cuando no, los detectores
permitían determinar u observar el camino
seguido por el fotón. El
resultado fue que, sin el bifurcador de emisiones,
el fotón tomaba un camino u otro, pero con él los detectores registraban interferencias. Para los
investigadores, este resultado acentuaba la controversia
sobre la influencia del observador en la física
cuántica, ya que: "podría dar a entender que alguna
fuente concebible estaba informando secretamente al
fotón de lo que debía hacer. Entonces debió mandarle un
mensaje que viajaba más rápido que la velocidad de la
luz, lo que está prohibido por las leyes de la
relatividad".
|
|
 |
|
|
|
|
Los fotones se
comportan como onda o partícula según el observador
(Publicado en la revista: Tendencias científicas, 23-02-2007) |
|
|
|
En 2012
se realizó otro experimento destinado a profundizar en
la interpretación de la pretendida naturaleza dual del fotón. En
este caso, se montó un dispositivo que
aprovecha una característica cuántica de todas las
partículas (incluidos los fotones), llamada
entrelazamiento: un conjunto
de partículas entrelazadas no pueden definirse como
partículas individuales con estados definidos, sino sólo
como un sistema con una función de onda única para todo
el sistema. Esta propiedad lleva a correlaciones entre las
propiedades físicas observables de las partículas
entrelazadas y, así por ejemplo, como dos fotones que nacen de
una misma fuente coherente están entrelazados, lo que
le ocurre a uno de ellos influye de forma instantánea a
lo que le ocurre al otro. |
|
|
|
 |
|
|
Aprovechando este hecho, se
entrelazaron dos fotones y se alternó en uno de
ellos el método de medida (como onda o como
partícula) para explorar en el otro la continua
mutación entre su comportamiento dual.
La interpretación de los investigadores fue
afirmar que "el fotón se comporta
simultáneamente como onda y como
partícula, lo que refuta los modelos en
que es una u otra". |
| |
|
"A Quantum Delayed-Choice Experiment"
(Artículo publicado en Science) |
| |
|
La
rareza cuántica de la luz como onda y como
partícula
(Noticia de prensa sobre el experimento) |
|
|
|
|
|
Para
terminar este apartado, nos referimos a la noticia que se publicó en 2015, acerca de otra
investigación en la que unos científicos de la Escuela
Politécnica Federal de Lausana (EPFL) en Suiza pudieron observar en una misma "fotografía" a la luz
comportándose como onda y como partícula. En el experimento, situaron un finísimo hilo
metálico (conductor) sobre una superficie de grafeno. Lanzaron haces de electrones sobre la
superficie de contacto entre ambos y al mismo tiempo,
iluminaron el hilo metálico con una luz láser
ultravioleta. Esta iluminación excita a los electrones
del hilo metálico, haciendo que se muevan colectivamente
por el hilo y liberen parte de la energía emitiendo
fotones en la dirección perpendicular a la superficie
del metal. |
|
|
|
 |
|
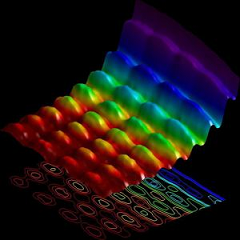
Así consiguieron, por una parte, que los
electrones incidentes colisionaran con los
fotones emitidos por el hilo y, por otra, que se
definieran en el hilo metálico regiones con
mayor número de electrones que ganan energía y
otras regiones donde el número es menor. La
imagen adjunta registra, por un lado, la
interacción entre los electrones incidentes
desde el exterior con los fotones emitidos por
el hilo conductor, lo que pondría en evidencia el
carácter corpuscular de esos fotones. Por otro
lado, la imagen también registra, un patrón de
interferencias, que pondría en evidencia el
carácter ondulatorio de los fotones generados
por una excitación electrónica colectiva del
metal (en este caso tienen una distribución atribuible a una
onda estacionaria en su interior).
"Simultaneous observation of the
quantizatLaion and the interference pattern of a
plasmonic near-fieldno"
(Artículo publicado en
Nature)
Primera
fotografía dual de la luz como partícula y como
onda
(Noticia
de prensa sobre el experimento) |
|
|
|
| |
|
|
| |
| |
Índice |
 |
|
|
|
| |
|
|
|