| |
|
 |
APLICACIÓN DE LA LEY DE CONSERVACIÓN DE LA CANTIDAD DE
MOVIMIENTO AL ESTUDIO DE COLISIONES |
 |
|
|
|
|
La ley de conservación de la cantidad de
movimiento es un principio general de la física que resulta de gran utilidad en la
resolución de problemas sobre sistemas de dos o
más partículas, ya que al imponer su verificación
se obtienen
relaciones que han de cumplir las masas y las
velocidades de las partículas, por ejemplo,
antes y después de una interacción (puede ser: una
colisión; la explosión de un proyectil en
varios pedazos; un proceso de fisión o de fusión
nuclear; etc..) Si se conocen las
masas y las velocidades de las partículas
antes de que interaccionen, se pueden predecir
así relaciones entre estas mismas magnitudes
después de que lo hayan hecho, y el problema
queda acotado (aunque no cerrado, porque también
se han de verificar otras relaciones,
como, por ejemplo, la ley de
conservación de la energía, si se trata de una
colisión perfectamente elástica). |
| |
|
Antes de
trabajar con algunos ejemplos de tales aplicaciones,
que los estudiantes analicen alguna situación
cotidiana y la interpreten aplicando
cualitativamente la ley de conservación del
impulso lineal. Una cuestión adecuada para ello, muy
interesante, puede ser considerar a una persona
que se coloca de pie encima de una balanza de
baño y rápidamente eleva una pierna (o, mejor,
los dos brazos), mientras observa el indicador
de la balanza. Posteriormente, puede repetir la
operación, pero agachándose se golpe (siempre
estando encima de la balanza de baño).
Podemos
pedir a los estudiantes que apliquen
cualitativamente la ley de conservación del
impulso lineal para explicar las indicaciones
que ha de marcar la balanza en estos procesos y,
también, pueden comprobarlo experimentalmente en
su casa. Encontramos esta cuestión (planteada y
resuelta) en la excelente página Web
Simple+mente Física, del profesor Rafael
García Molina, quien también es el autor de la
bonita ilustración adjunta que la acompaña.
(Documento original
aquí) |
|
 |
|
| |
|
|
|
Nos referimos ahora el caso particular de choque elástico entre dos
bolas, que ilustra la animación Modellus
adjunta.
La bola roja se dirige hacia la otra bola (amarilla) y
se supone que, después de chocar ambas, la primera
queda en reposo.
Se exige también que ambas
bolas se vean obligadas a moverse
en la misma dirección (prefijada, por ejemplo,
por un canal). Después de plantear así el
problema a los alumnos, podemos pedirles que lo
resuelvan mediante un proceso de investigación,
en cuyo desarrollo pueden usar la
animación para contrastar hipótesis y algunos casos
límite, ya que, como vemos, en la pantalla de la
misma se
dispone de tres controladores manuales con los
que se pueden modificar a voluntad las masas de las
dos bolas y la velocidad de la que se lanza (roja).
Clic
aquí para descargar esta animación [Si
no lo tienes instala
Modellus] |
|
|
|
|
Terminado el problema y, a modo de ampliación del
mismo, puede resultar muy instructivo que los alumnos vean y
analicen la
figura animada adjunta.
Esta
figura animada (el video original procede de la
Web oficial del programa Tracker) enseña que
una colisión entre dos partículas puede
implicar una amplia variedad de situaciones
dinámicas diferentes,
más allá del caso particular que acabamos de
estudiar. Los alumnos pueden analizar esta
figura animada con objeto de identificar algunos
de los
muchos factores que pueden influir en el
movimiento que tengan las partículas tras la
colisión, tales como: el hecho de que el choque
sea o no elástico
(dicho de otro modo, que se conserve o no la energía)
y, en caso de que no lo sea, el porcentaje de energía que se
pueda perder durante la interacción; el hecho de
que las partículas se
pueden trasladar (antes y/o después de chocar) en una, en dos o en tres
dimensiones; la posibilidad de que durante sus
movimientos de traslación la partículas
(individuales o agrupadas) puedan realizar
también movimientos de rotación interna; el
hecho de que la colisión sea frontal o, que, por
el contrario, una
partícula choque contra la otra lateralmente y
la empuje hacia una dirección oblicua a la de
entrada; el hecho de que las partículas puedan quedar pegadas
tras el choque; etc. |
|
 |
|
|
|
|
 |
|
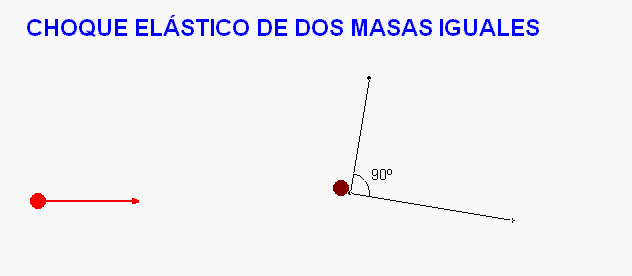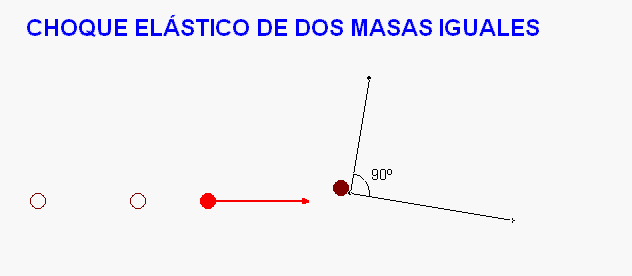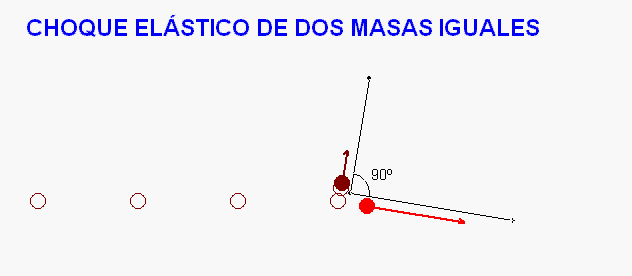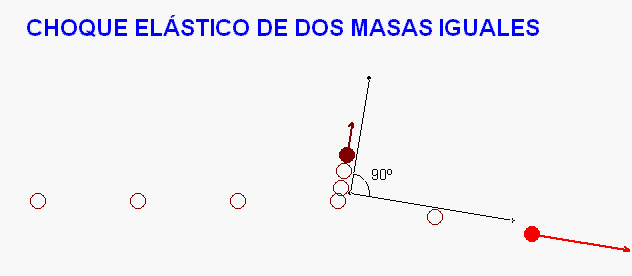
Entre todos
los casos posibles, nos
detenemos ahora en uno particular, que resuelve
la animación Modellus adjunta.
Ocurre cuando
colisionan dos partículas de
masas iguales y que se puedan desplazar
libremente en un
plano. Si el choque es elástico y no hay
rotación interna de las partículas (de tal forma
que cada una de ellas se puede reducir a un
"punto material"), tras exigir el cumplimiento de
la ley de conservación del impulso y de la ley
de conservación de la energía mecánica, se
deduce (en el marco de la mecánica newtoniana)
que el ángulo de salida tras la
colisión ha de ser de 90º.
Clic
aquí
para descargar esta animación. |
|
|
|
|
Ahora
bien, conviene recordar que la mecánica newtoniana deja
de ser aplicable si las partículas tienen velocidades muy elevadas, que puedan ser
comparables a la velocidad de la luz. Y esto es lo que
realmente ocurre en algunos procesos que implican colisiones elásticas entre
dos partículas subatómicas (pueden ser, por ejemplo: dos
electrones, dos protones,..), en los que el problema se ha de tratar
en el marco de la
relatividad especial. Pues bien, en estos casos el
ángulo de salida tras la interacción no es de 90º, sino
menor. |
|
|
|
Dicho de otro
modo:
la solución más correcta de
este
problema que proporciona la teoría relativista
(un ángulo inferior a 90º) se separa de la que proporciona la mecánica
newtoniana (90º), tanto más, cuanto mayores sean las
velocidades de las partículas implicadas en la
colisión. La fotografía adjunta (a la derecha)
corresponde a la colisión de un protón incidente
con energía del orden de 5MeV con otro protón,
inicialmente en reposo, en una emulsión
fotográfica. El choque en este caso fue “no
relativista” y, como se observa muy
claramente, se obtuvo un ángulo experimental muy
próximo a los esperados 90º entre las trayectorias de salida
de los protones después del choque.
Clic
aquí para
descargar un documento textual donde se resuelve este problema
en el marco de ambas teorías. |
|
 |
|
|
|
|
|
|
Vamos
ahora a comentar otro problema sencillo que se puede tratar en
clase, del que también hemos elaborado
una animación interactiva Modellus
Un cañón dispara una bala y ésta se
incrusta en un bloque de determinado material. El conjunto
bloque-bala incrustada sale
despedido y nos planteamos con qué velocidad lo
hace. Para resolver el problema, los alumnos han
de exigir el cumplimiento de
la ley de conservación del impulso y pueden plantear
hipótesis y considerar algunos casos límite.
La animación resuelve el problema y, como vemos, permite
modificar la velocidad a la que se dispara la
bala, su masa y la masa del bloque.
Clic
aquí para descargar esta animación [Si
no lo tienes instala
Modellus] |
|
| |
|
Finalmente, después de
haber desarrollado
algunos de estos problemas
que involucran a la ley de conservación de la cantidad
de movimiento, se pueden complementar estos estudios,
con la
realización
trabajos experimentales (cualitativos y
cuantitativos) sobre choques y rebotes. |
|
| |
Índice |
 |
|
|
|
|
|
|