| |
|
 |
LEYES DE
LOS GASES |
 |
|
|
|
| |
|
El modelo cinético-corpuscular de los gases
implica que la presión, P,
el volumen, V, la temperatura, T, y la cantidad de
gas (que vamos a caracterizar por el número de partículas, N)
han de ser magnitudes interdependientes. Nos planteamos ahora profundizar en
el modelo para expresar de forma operativa esas dependencias y
ello nos lleva a escribir las siguientes leyes de los gases: |
|
|
|
a) Ley
de Boyle y de Mariotte: Si la cantidad de gas y la temperatura
permanecen constantes, podemos esperar que la presión disminuya
al aumentar el volumen. Esto es así porque al aumentar el volumen
disminuye la densidad de partículas y, por tanto, ha de
disminuir la frecuencia de sus choques con las paredes del
recipiente. De forma
más precisa, planteamos que en estas condiciones el
volumen, V, debe
ser inversamente proporcional a la presión, P (P
· V = k , para T y N constantes). |
| |
|
Para
reforzar el estudio de esta relación de proporcionalidad
inversa entre la presión y el volumen de un gas, se
puede usar en clase la animación adjunta.
Como
vemos, con el controlador manual disponible en la
pantalla, podemos ir modificando el valor de la presión
de un gas y la animación va calculando el
correspondiente volumen y representando gráficamente la
relación V = f (T). En cualquier momento podemos
detener este proceso e incorporar unos valores
diferentes de la temperatura y de la cantidad de
sustancia. Entonces, obviamente, cambia el valor de la
constante k de la ley de Boyle y se dibuja por el mismo
procedimiento una nueva gráfica
de la relación V = f (T) desplazada con respecto
a la gráfica
anterior, y, que, por supuesto, sigue reflejando una
función de proporcionalidad inversa.
Clic
aquí para descargar la animación. Recuerda que para
usarla en tu ordenador necesitas descargar
Modellus 2.5
(ordenadores de 32 bits) o
Modellus 3 (64 bits)
|
|
 |
|
| |
|
Boyle (1627
- 1691) |
|
En 1657
Boyle
(1627-1691), físico y químico irlandés, se
interesó por la bomba de aire, con la que su
inventor
Otto von
Guericke (1602-1686) había
realizado en 1654 un experimento espectacular
que puso de manifiesto la magnitud de la presión
del aire (los
hemisferios de Magdeburgo).
Con la ayuda de
Hooke
(1635-1703), Boyle perfeccionó aquella bomba de
aire hasta obtener, en 1659, una máquina
neumática, que le sirvió para realizar
importantes experimentos (investigó el
comportamiento del aire, estudió la
caída
de los cuerpos en ausencia de rozamiento y
la no transmisión del sonido en el
vacío). En los experimentos dedicados a estudiar el comportamiento del aire
comprobó que dicho aire
es comprimible y elástico ("si se elimina la
presión, el aire recupera su volumen original")
y afirmó su naturaleza cinético-corpuscular. |
|
|
|
|
El
físico francés
Mariotte (1620-1684) también estudió
la compresión de los gases y obtuvo, por su parte, la
misma ley que relaciona
la presión con el volumen, si bien no publicó sus
estudios hasta 1976. |
|
|
|
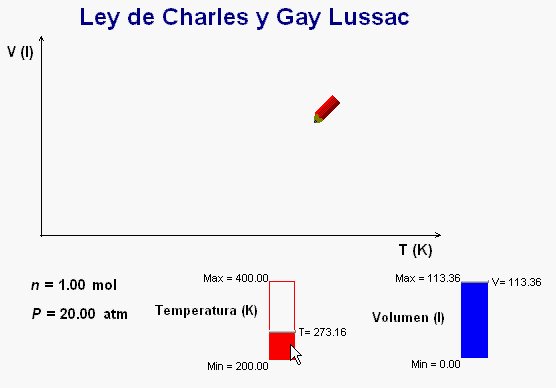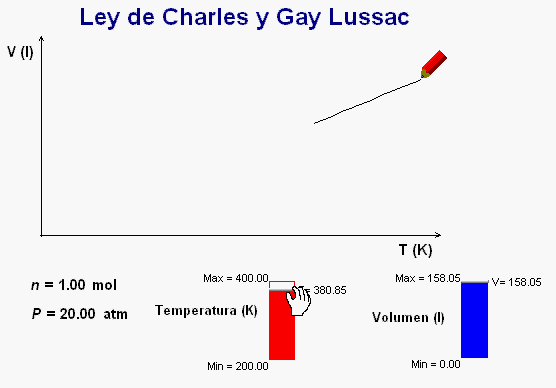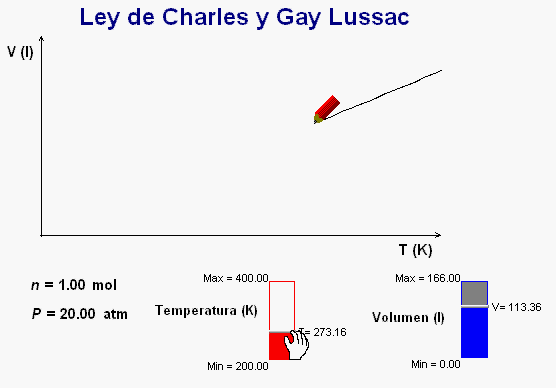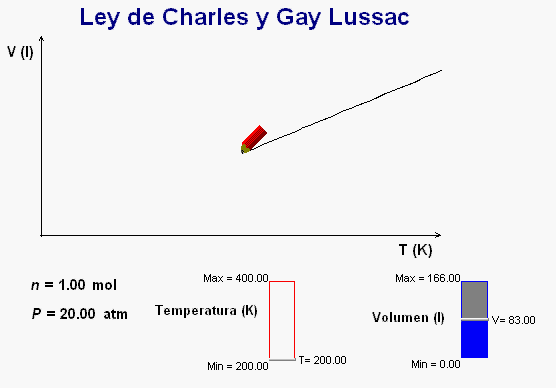
b)
Ley de Charles y de Gay-Lussac: Si la cantidad de
gas y la presión permanecen constantes, es razonable
suponer que el volumen aumente al aumentar la
temperatura. Un aumento de temperatura implica un
incremento de la energía cinética media de las
partículas, por tanto, un aumento de su velocidad y de
la frecuencia e intensidad de los choques de éstas con
las paredes. Si la pared es elástica (por ejemplo, un
globo) o se puede desplazar (por ejemplo, un embolo) y
la presión exterior (que iguala a la interior) permanece
constante, se plantea que el volumen del gas, V, debe ser
proporcional a su temperatura, T (V
= K · T , para P y N constantes). |
|
| |
|
En clase
también podemos reforzar el estudio de esta ley con
la animación adjunta, que funciona de una manera similar
a la anteriormente comentada.
Como vemos,
al ir modificando la temperatura del gas, la animación
va dibujando una gráfica de la relación entre la
temperatura y la presión, cuyo perfil corresponde a la relación de
proporcionalidad directa que han de cumplir estas dos
magnitudes. Obsérvese, por otra parte, que la animación no
nos permite dar a la temperatura
valore inferiores a 200K. Esto tiene que ser así porque, como
acabamos de comentar, si la temperatura fuera muy baja,
también lo sería la energía cinética media de las
partículas y entonces el gas dejaría de comportarse como
plantea que debería hacerlo el modelo
cinético-corpuscular.
Clic
aquí para descargar la animación. Para usarla en tu
ordenador necesitas descargar
Modellus 2.5
(ordenadores de 32 bits) o
Modellus 3 (64 bits) |
|
 |
|
| |
|
 |
|
Gay-Lussac (1778 - 1850) |
|
|
Gay-Lussac (1778
- 1850), químico y físico francés, publicó en 1802 esta
ley de la relación entre la temperatura y la presión de
un gas, haciendo referencia a un trabajo anterior no
publicado de
Charles (1746-1823), el inventor, científico y matemático francés que
había realizado el primer viaje en globo aerostático (en
1783). La ley también había sido anticipada cien
años antes de la publicación de Gay-Lussac (en 1702) por
otro físico e inventor francés,
Amontons (1663-1705).
Gay-Lussac
también estudió la relación entre la presión y la
temperatura, formulando lo que se conoce como su segunda ley. |
|
|
|
|
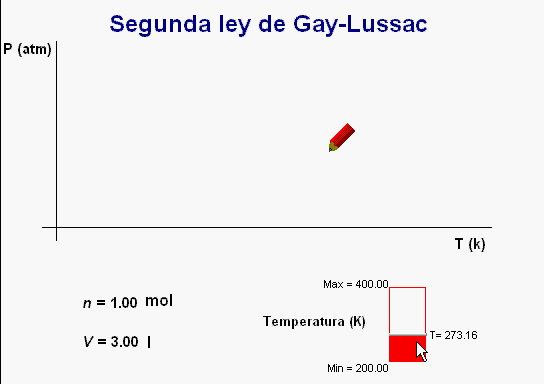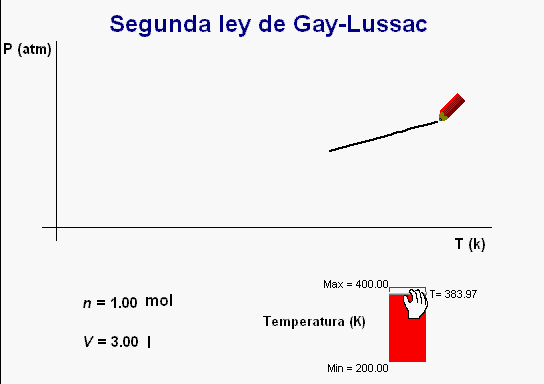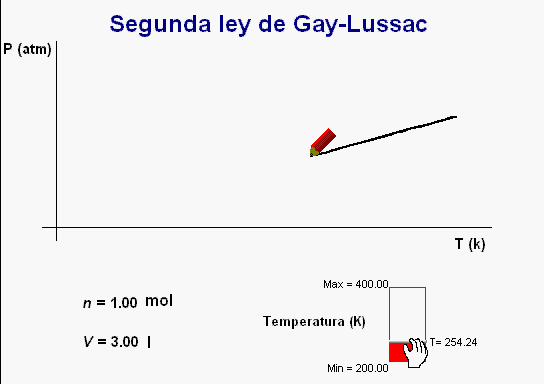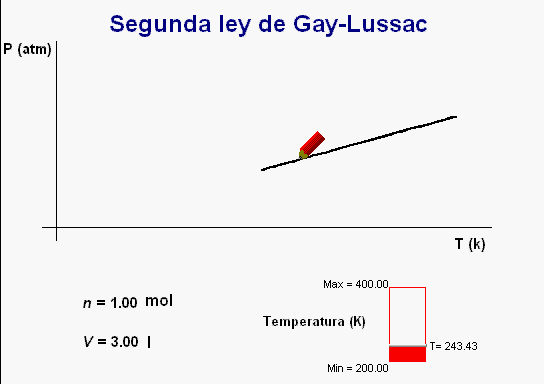
c)
Segunda ley de Gay-Lussac: Si la cantidad de gas y el
volumen permanecen constantes, es lógico suponer que la presión
aumente al aumentar la temperatura, puesto que, como ya sabemos, un aumento de temperatura implica un aumento de la
velocidad de las partículas y, en consecuencia, de la frecuencia
e intensidad de los choques de ellas con las paredes.
Matemáticamente expresamos que la
presión, P, debe ser proporcional a la temperatura (P
= k · T , para V y N constantes) |
|
|
|
Igual
que ocurre con
las dos leyes anteriores, también podemos
reforzar el estudio de la segunda ley de Gay-Lussac con
la animación adjunta.
Como vemos,
al operar de manera similar a los casos anteriores, la
animación va dibujando una
gráfica de la relación entre la temperatura y la presión
del gas, cuyo perfil se corresponde con la relación de
proporcionalidad directa que han de cumplir estas dos
magnitudes. También ocurre aquí que la animación no nos permite dar
a la temperatura valores inferiores a 200K, para los
cuales el gas dejaría de comportarse como
predice el modelo cinético-corpuscular.
Clic
aquí para descargar la animación. Para usarla en tu
ordenador necesitas descargar
Modellus 2.5
(ordenadores de 32 bits) o
Modellus 3 (64 bits) |
|
 |
|
|
|
|
d) Influencia
del número de partículas: A igualdad de volumen y
temperatura, cabe esperar que la presión de un gas aumente al
aumentar el número de partículas. Aumentar el número de
partículas implica aumentar el número de choques por unidad de
tiempo y de superficie. Planteamos, por ello, que la presión, P,
debe ser proporcional al número de partículas (P = k · N,
para V y T constantes) |
| |
|
El conjunto de
leyes sobre el comportamiento que deberían tener los gases en
coherencia con el modelo cinético-corpuscular se puede resumir
agupando todas las dependencias ya vistas en una sola
expresión que relaciona las cuatro variables macroscópicas que
determinan el estado del gas. Esta expresión es: |
| |
|
 |
| |
|
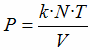Se conoce
como ley de los gases ideales o
ley de los gases perfectos,
puesto que los gases deberían
verificarla estrictamente si su comportamiento se atuviera a todas las condiciones que exige el modelo cinético
corpuscular. |
| |
|
Diremos finalmente que la constante K que aparece en la ley de los
gases es una constante universal, llamada constante de Boltzman. Para estudiar
procesos químicos donde intervienen sustancias en estado
gaseoso es más útil expresar la cantidad de gas por el
número de
moles, n, en lugar de por el número de partículas, N.
Ambas magnitudes se relacionan mediante la expresión N =
n·NA
(NA
es el
número de Avogadro), con lo que la ley de los gases se
expresa PV = knNAT
o, en la forma más usual, PV = nRT. (La
constante R = K·NA
se llama constante universal de los gases ideales). |
|
|
|