|
 |
MOVIMIENTOS ORBITALES II. TRAYECTORIA ELÍPTICA. LEYES DE KEPLER |
 |
|
|
|
|
|
|
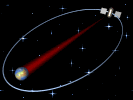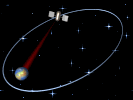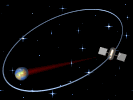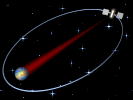
Muchas veces los
cuerpos sometidos al campo
gravitatorio producido por un cuerpo celeste siguen
una trayectoria elíptica, estando
situado la estrella o el planeta que produce el campo en
uno de los focos de la elipse. Este
movimiento lo realizan, por ejemplo, los
satélites
terrestres de la órbita HEO, los
planetas del Sistema Solar,
los cometas, unas galaxias respecto de otras, etc. Las órbitas elípticas se recorren
con una velocidad variable, mayor cuanto más
cerca se está del cuerpo que
produce el campo y menor cuanto más alejado se
está de él. |
|
 |
|
|
|
|
|
|
Entre 1609 y 1619
Kepler (1571-1630)
formuló tres leyes sobre el
movimiento de los planetas alrededor del Sol, que son
generalizables al movimiento elíptico de
cualquier cuerpo sometido al campo gravitatorio de otro.
Kepler había pasado una gran parte de su vida tratando
de comprender cómo se mueven los planetas, intuyendo que
debían seguir algún tipo de ley. Por otra parte, el
astrónomo danés
Tycho Brahe (1546-1601)
había acumulado un conjunto amplio de observaciones
sistemáticas de dichos movimientos. Después de la muerte
de Tycho, su familia le facilitó esos datos a Kepler,
que realizó
un importante trabajo de síntesis para formular sus tres leyes: |
|
|
|
|
Primera Ley
(1609): Los planetas se desplazan alrededor
del Sol describiendo órbitas elípticas, estando
el Sol situado en uno de los focos.
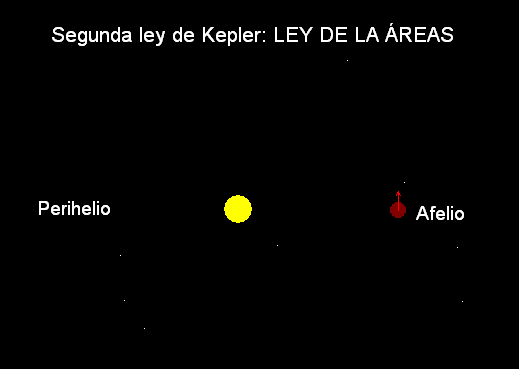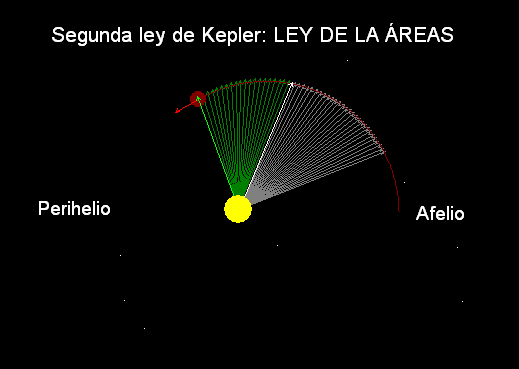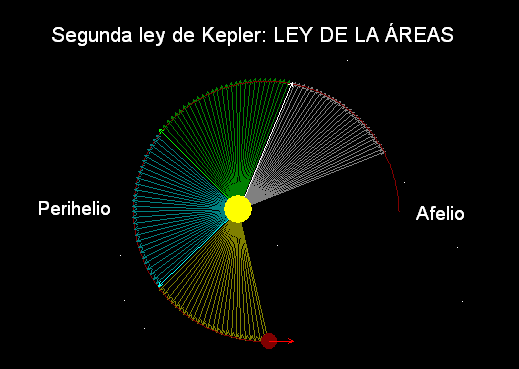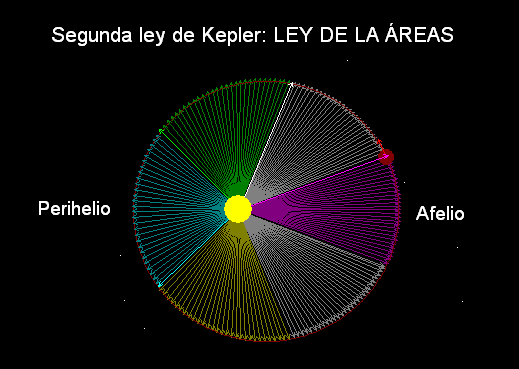
Segunda Ley
(1609): El radio vector que une el planeta y
el Sol barre áreas iguales en tiempos iguales
(tal como ilustra la animación Modellus adjunta).
Esto concuerda con el hecho de que el
movimiento es más rápido en la zona en la que el
planeta pasa más cerca del Sol, alrededor del
perihelio, y más lento en la
zona opuesta, alrededor del afelio).
Tercera Ley
(1619): Para cualquier planeta, el cuadrado
de su período orbital (tiempo que tarda en dar
una vuelta alrededor del Sol) es directamente
proporcional al cubo de la distancia media con
el Sol
1619. Las tres leyes de Kepler
Artículo del
Dr.
D. Rafael Bachiller
(Febrero de 2009)
|
|
|
|
|
|
|
Aunque resultó muy
satisfactorio encontrar tales leyes, Kepler nunca
consiguió comprender el sentido último de las mismas.
Posteriormente, con el desarrollo de la teoría de Newton
de la Mecánica y la
Ley de la Gravitación Universal, las leyes de Kepler se
pudieron interpretar como un resultado natural de la
interacción entre el Sol y cada planeta. |
|
|
|
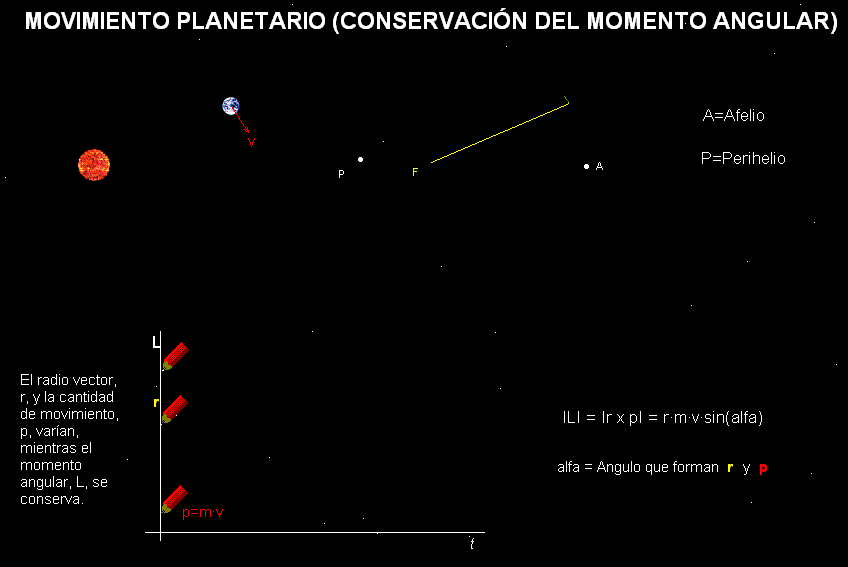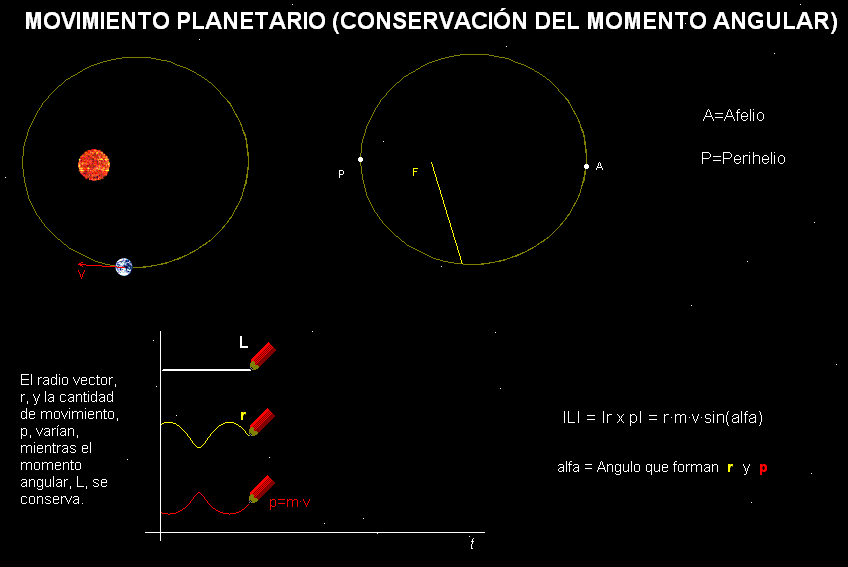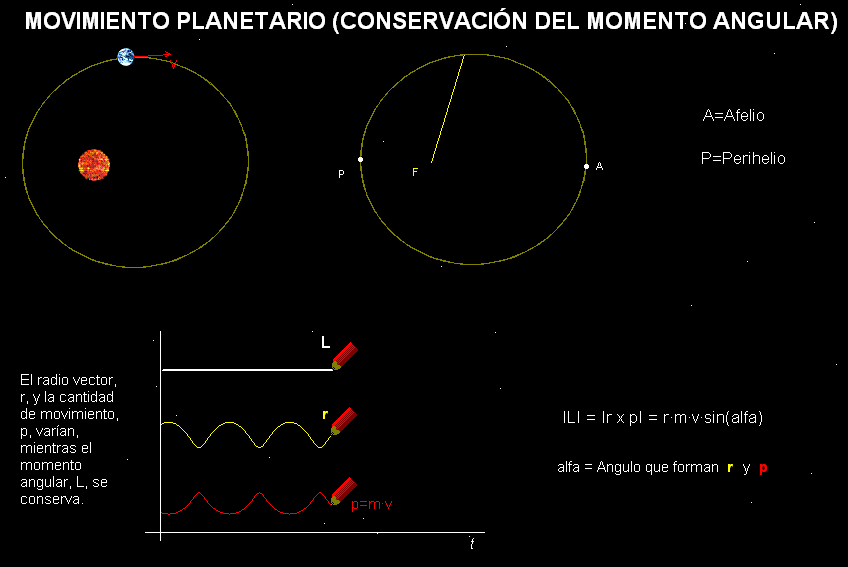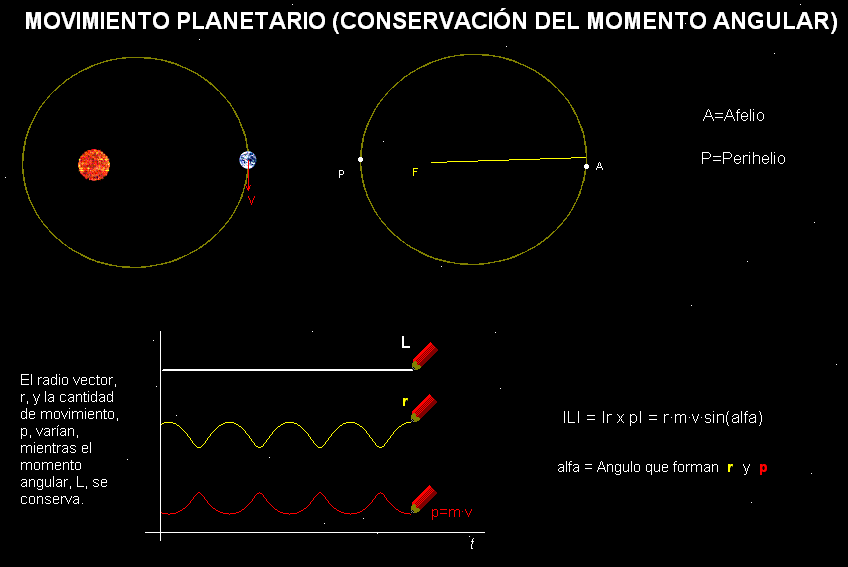
Esta animación
(debajo) recrea el movimiento de traslación de la
Tierra con respecto al Sol. Su modelo
físico-matemático consta de Ley de
Gravitación Universal y de las leyes de Newton de la Mecánica. La simulación constata que, en un rango de
valores de la velocidad inicial, la trayectoria
es elíptica y también que, mientras el radio
vector que indica la posición de la Tierra y la
cantidad de movimiento de nuestro planeta
varían, el momento angular permanece
constante. De hecho, la exigencia de que se
cumpla el principio de conservación del
momento angular permite deducir la segunda ley de
Kepler. Dicha ley también se puede prever
cualitativamente mediante un análisis acerca de la
orientación que tienen en cada punto de la
órbita planetaria la aceleración del planeta
y sus componentes normal y tangencial (deducciones en
este
documento). |
|
|
|
 |
|
Clic
aquí para descargar esta animación [Si no lo
tienes instala
Modellus 2.5 (32 bits) o
Modellus 3
(64 bits)] |
|
|
|
También la tercera
ley de Kepler se deduce directamente al aplicar
la Mecánica de Newton al movimiento planetario,
y se obtiene el siguiente valor de la constante
de la ley de Kepler (deducción en
este documento,
suponiendo órbitas circulares):
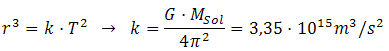
En Astronomía, al
referirnos al Sistema Solar, se suelen
expresar las distancias en unidades astronómicas
(ua), habiendo definido una unidad astronómica como una
medida de longitud igual al radio medio de la
órbita terrestre. Al expresar
el periodo orbital en años, la constante de
Kepler se hace igual a 1 (k= 1ua3/años2),
con lo que, tanto el radio de la órbita
terrestre, como el periodo orbital de la Tierra,
sirven de referencia para el resto de planetas del
Sistema Solar. |
|
 |
|
|
|
|
La siguiente animación (debajo) utiliza la tercera ley de Kepler como
modelo físico-matemático para gobernar el
movimiento de los planetas con respecto al Sol.
Entrando en la ventana de condiciones iniciales
y también mediante un cursor situado en la
pantalla, permite atribuir al radio de la
órbita (supuesta circular) un valor que puede
oscilar desde el radio medio de la órbita de
Mercurio hasta el radio medio de la órbita de Marte. La
simulación obtiene los valores correspondientes
de los periodos de los cuatro primeros planetas
del sistema solar y de sus velocidades de
traslación alrededor del Sol, constatando que
coinciden con los valores reales. |
|
|
|
 |
|
Clic
aquí para descargar esta animación [Si no lo
tienes instala
Modellus 2.5 (32 bits) o
Modellus 3
(64 bits)] |
|
|
|
Para cualquier otro objeto
describiendo una órbita elíptica alrededor de un cuerpo
celeste, la constante de Kepler se calcula igual,
después de sustituir en la expresión anterior la masa
del Sol por la masa del cuerpo que produce el campo (por
ejemplo, se sustituirá la masa de la Tierra si se quiere
saber la relación entre el periodo y el radio de las
órbitas de nuestros satélites). |
|
|
|
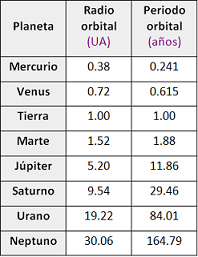
Tabla de datos de los planetas del Sistema Solar |
