Teniendo en cuenta este resultado es interesante imaginar el movimiento que tendría un objeto al que dejáramos caer por el interior de un túnel hipotético que atravesara a la Tierra completamente (desde un punto de su superficie hasta otro situado en sus antípodas): La velocidad del cuerpo aumentaría durante la caída hasta que el objeto llegara al centro de la Tierra.  A partir de ahí, la velocidad del cuerpo disminuiría paulatinamente para volver a ser nula al llegar a la superficie en el punto situado en las antípodas del lugar donde se inició el movimiento. Seguidamente el movimiento continuaría en sentido opuesto, repitiendo las mismas pautas que a la ida para terminar alcanzando, otra vez con velocidad cero, el lugar de lanzamiento. En ese instante el movimiento habría cubierto un ciclo completo que, en ausencia de rozamiento, se repetiría una y otra vez.

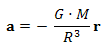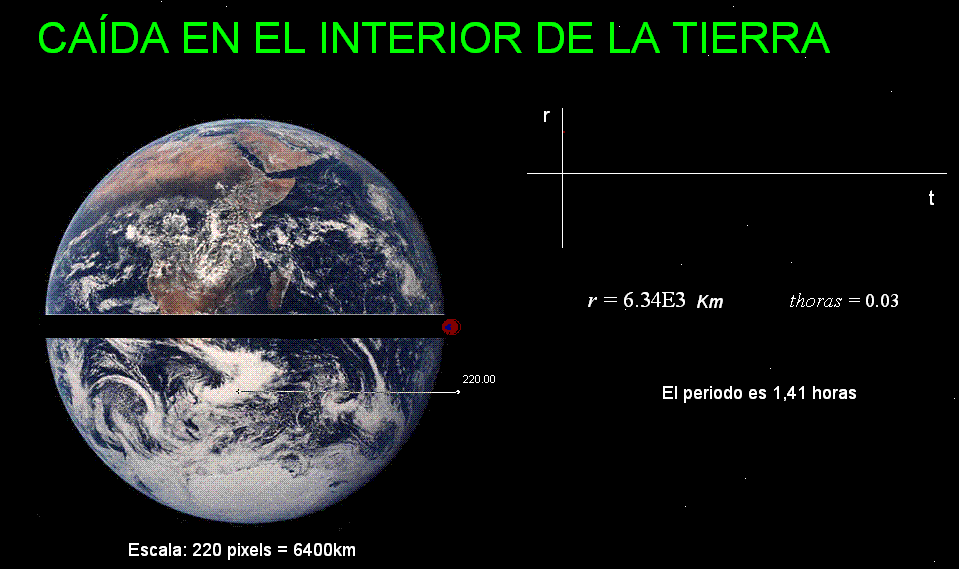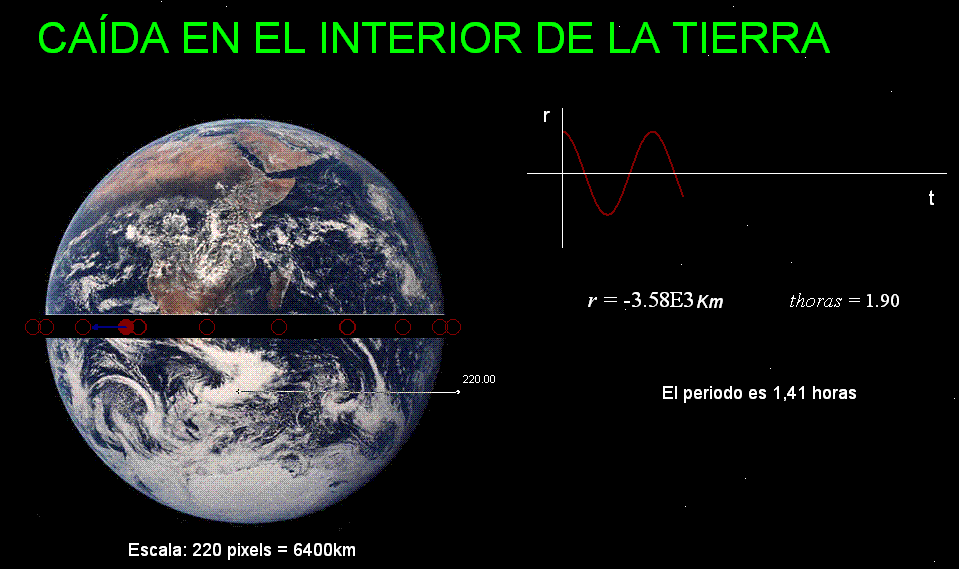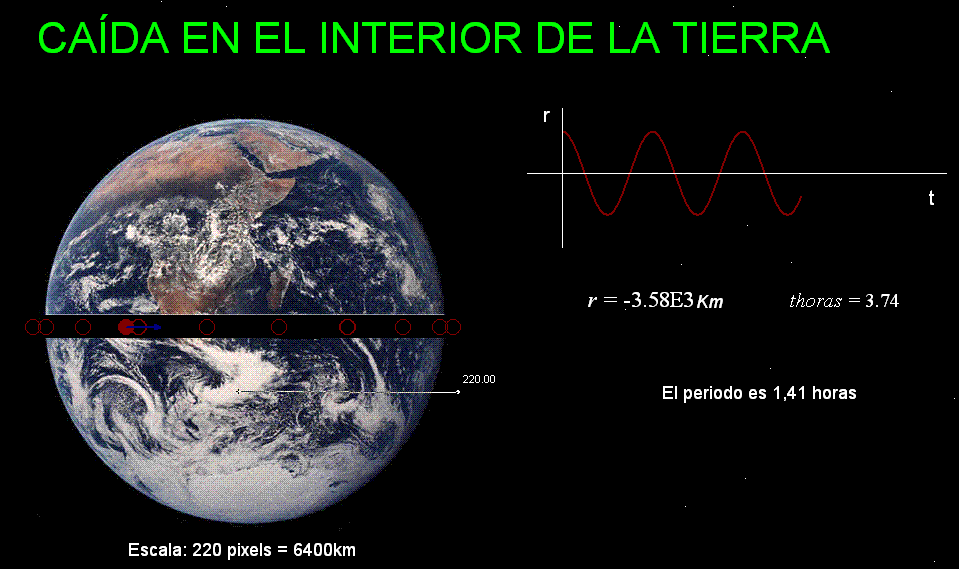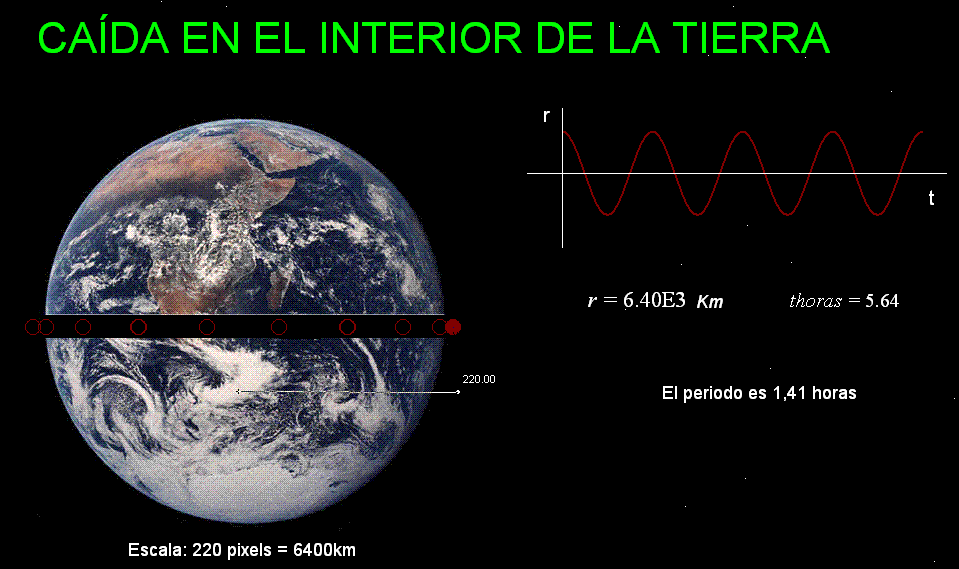
Por tanto, usando el concepto de que la aceleración del movimiento armónico simple se expresa por, a=-w²r, se concluye que dicho movimiento de oscilación sería armónico simple. Aplicando los valores de la masa de la Tierra, el radio terrestre y la constante de gravitación se obtiene (ver documento) para el mismo un periodo de 1.41 horas.

Clic  aquí para descargar la animación [Si no lo tienes instala Modellus 2.5 (32 bits) o Modellus 3 (64 bits)]