VELOCIDAD DE ESCAPE Y ATMÓSFERAS PLANETARIAS

 

Hemos definido la velocidad de escape, como la velocidad mínima que debe tener un cuerpo para que escape de la atracción gravitatoria de la Tierra, o de cualquier cuerpo celeste. En la superficie de un cuerpo celeste de masa M y radio R, dicha velocidad vale (deducción en este documento):

 
 

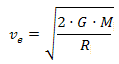Lógicamente, la velocidad de escape en la superficie de un cuerpo celeste es mayor cuanto mayor sea la masa, M, del mismo y menor cuanto mayor sea su radio R.
 

En la superficie de la Tierra, se obtiene una velocidad de escape del orden de 11.2 km/s, tal como se muestra a la derecha de este texto.

  

 

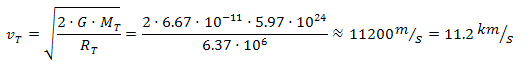Interesa relacionar este dato con la temperatura en la superficie de nuestro planeta, ya que ambos parámetros son determinantes para justificar la formación y el mantenimiento de la atmósfera terrestre, así como el tipo de atmósfera existente.

 
 

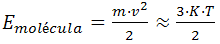Para hacerlo, usamos la teoría cinética de los gases, según la cual la energía cinética, Ec, de una molécula de masa m de un gas se relaciona con su velocidad, v, y con la temperatura absoluta, T, del mismo, mediante la expresión adjunta (donde K es la constante de Boltzman).
 

Partiendo de esta relación se deduce una velocidad típica  de una molécula de gas a una determinada temperatura, dada por la expresión:

 

 

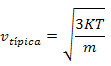Matemáticamente la velocidad típica es una velocidad cuadrática media o, lo que es igual, es la raíz cuadrada del cuadrado de la velocidad media.
 

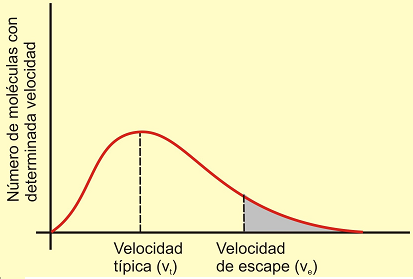
La velocidad típica asignable a las moléculas de un gas representa a un valor de un amplio rango de velocidades que pueden tener las diferentes moléculas. Si se considera al gas como gas perfecto, las velocidades de todas las moléculas muestran un tipo de distribución estadística "maxwelliana", como la indicada en la gráfica adjunta. Por tanto, aunque la velocidad de escape sea mayor que la velocidad típica, normalmente siempre siempre va a haber un porcentaje de moléculas con velocidades mayores y que, en consecuencia, escapan (zona sombreada de la gráfica).

En estas condiciones, las leyes de la estadística establecen como un criterio adecuado para que un planeta retenga su atmósfera durante mucho tiempo el requisito de que la velocidad de escape no supere en más de 6 veces a la velocidad típica (vescape > 6·vtípica)

  

 

 

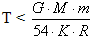Teniendo en cuenta las expresiones que calculan respectivamente la velocidad de escape y la velocidad cuadrática media, se deduce la expresión adjunta que indica el valor límite que ha de tener la temperatura superficial de un planeta, T, para retener durante mucho tiempo a las moléculas de una determinada masa, m que forman su atmósfera. 

 

Por tanto, la temperatura superficial de un planeta o de un satélite resulta crucial, tanto para determinar la formación y la evolución de su posible atmósfera, como para explicar la composición química de dicha atmósfera.
 

 

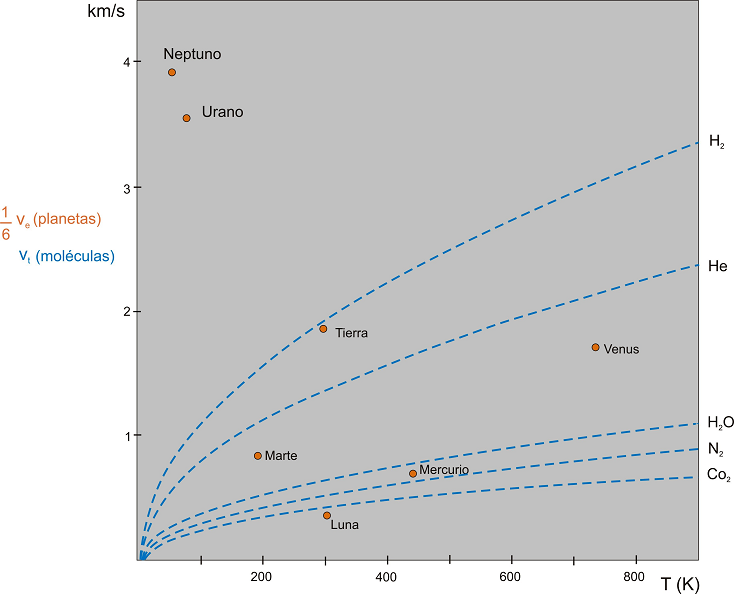
Considerando estos desarrollos, es interesante construir el gráfico adjunto donde se representa velocidad frente a temperatura y empezar ubicando en él diversos astros del sistema solar, según sus valores de sus temperaturas superficiales T y 1/6 de sus velocidades de escape.
 

A continuación, se pueden trazar en ese mismo gráfico unas líneas (punteadas) que marquen los valores de la velocidad típica vt de las moléculas en función de la temperatura, T, para algunos de los principales candidatos a ser componentes de una atmósfera (como puede observarse, no hemos incluido a Júpiter ni a Saturno, que exigirían un rango mucho mayor en ordenadas; tampoco hemos considerado al oxígeno, cuyos valores son muy similares al nitrógeno). Si un astro, caracterizado por una temperatura superficial dada, se ubica por encima la línea correspondiente a un determinado gas, se cumplirá que ve/6 es mayor que vt (a dicha temperatura) y, por tanto, podrá retenerlo.
 

Problema como investigación y animaciones interactivas sobre la velocidad de escape
 

Estudio de la velocidad de escape. Un problema como investigación. Artículo publicado en la revista Alambique. Didáctica de las Ciencias Experimentales (Manuel Alonso, Jaime Carrascosa y Salvador Martínez)

 

Así vemos que las atmósferas de los planetas jovianos (Júpiter, Saturno, Urano y Neptuno) están dominadas por elementos ligeros, principalmente H2 y He, que son los gases más abundantes en el Sistema Solar. Son, por tanto, atmósferas primarias, que se crearon cuando se formó del Sistema Solar. En cambio, las atmósferas de los planetas terrestres, que las tienen (Venus, Tierra y Marte), son atmósferas secundarias, dominadas por moléculas como CO2, N2 y O2 (en la atmósfera de la Tierra predominan el nitrógeno, N2, con una abundancia del 78.08%, y el oxígeno, O2, con una abundancia del 20.95%). Estos planetas, tras su formación, también tenían una atmósfera primaria compuesta principalmente de H2 y He. Pero, como enseña el gráfico anterior, ambos gases son muy livianos y poco a poco se perdieron hacia el espacio. En la Tierra las erupciones volcánicas inyectaron a aquella atmósfera primitiva sustancias como H20, CO2, SO2, N2, S2 y SOx. Posteriormente, al enfriarse los gases volcánicos sólo una mínima fracción del agua pudo permanecer en estado de vapor en el aire. El resto formó nubes y precipitaciones muy abundantes que propiciaron la formación de los océanos.

  

 

Las lluvias, muy abundantes, eliminaron la mayor parte del CO2 de la atmósfera al disolverse en el agua para formar ácido carbónico que reaccionó con las rocas originando carbonatos. El nitrógeno, N2, pasó a ser mayoritario (aproximadamente, el 20 % del N2 volcánico se fijó al suelo por microorganismos, mientras el resto se acumuló en el aire por su débil reactividad química y baja solubilidad en agua) y el oxígeno, O2, comenzó a formarse a partir del agua líquida, mediante procesos de foto-disociación [2H2O + UV = 2H2 + O2] y de foto-síntesis [H2O + CO2 + VIS = {CH2O} + O2], que se originó en organismos unicelulares a una profundidad marina donde llegaba la radiación visible (VIS), pero no la radiación ultravioleta (UV).