| |
|
 |
CONCEPTO
DE CAMPO ELÉCTRICO |
 |
|
|
|
|
|
|
Para interpretar la acción a
distancia ejercida por las cargas eléctricas se requiere el
concepto de campo,
en este caso el campo eléctrico. |
|
|
|
|
|
La animación adjunta
reproduce el procedimiento que se ha de seguir para
representar el campo eléctrico creado por una carga puntual,
Q . Colocamos en varios puntos alrededor de la
carga, Q, otra carga, q, positiva, a la que llamamos
carga testigo o carga de prueba. En cada lugar, la carga que crea el
campo, Q, ejerce una determinada
fuerza eléctrica, Fe sobre la carga testigo,
q.
Por definición, el campo electrostático en cada punto,
E,
es igual al cociente entre la fuerza ejercida sobre la
carga testigo colocada ahí y el valor de dicha carga de
prueba (E=Fe/q ; Fe=q·E).
Por lo tanto, el campo, E, se representa mediante un vector
que tiene la misma
orientación que la fuerza que sufre la carga
testigo positiva y una longitud proporcional al valor de su
intensidad, E.
Clic
aquí para descargar esta animación [Si no lo
tienes instala
Modellus 2.5 (32 bits) o
Modellus 3
(64 bits)] |
|
|
|
|
Siguiendo este
procedimiento llenamos el espacio circundante a la carga
Q
de vectores que indican el campo que produce y la totalidad de tales
vectores representa al campo electrostático en esa región. Las
líneas
de fuerza se trazan dibujando líneas tangentes a dichos vectores.
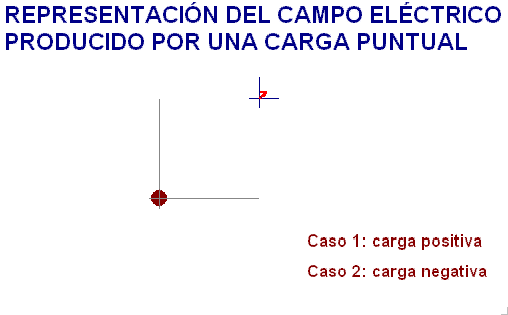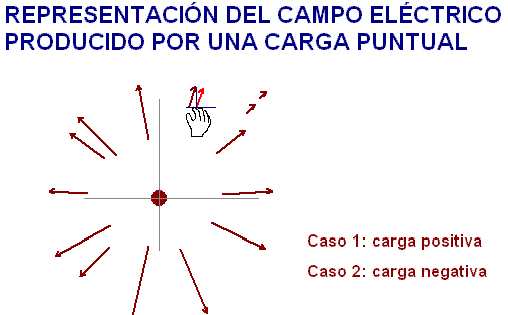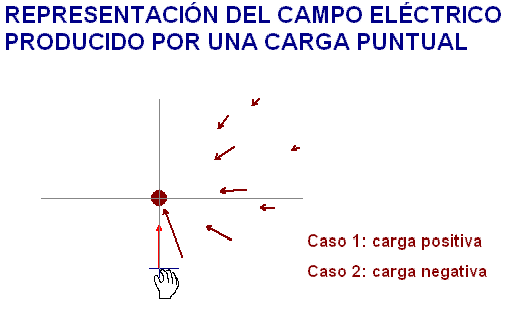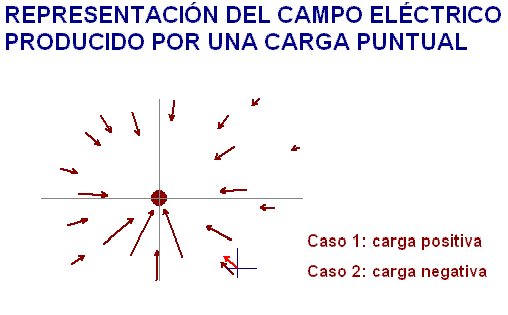
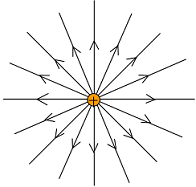
La representación
obtenida muestra que el campo producido por una
carga puntual es
radial. Es decir, sus líneas son abiertas y forman un haz
centrado en la
carga que lo crea. Si dicha carga es positiva, la
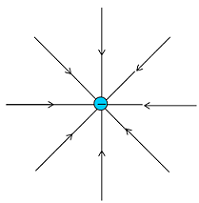
líneas "nacen" de ella y se dirigen hacia el infinito.
Si la carga productora del campo es negativa, las
líneas vienen desde el infinito para "morir" en
ella. |
|
 |
|
 |
|
|
|
|
Para obtener la
expresión que calcula el campo eléctrico en cada punto
alrededor de la carga, Q, reiteramos el
procedimiento de colocar ahí la carga de prueba, q,
y luego dividir la fuerza
que sufre dicha carga de prueba, entre la propia carga, q.
Se obtiene que el campo eléctrico producido por
una carga puntual,
Q, a una cierta distancia, r,
vale: |
|
 |
|
|
|
|
|
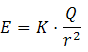El campo
eléctrico puede ser
creado
por varias cargas.
Entonces, el vector que representa al
campo resultante en cada punto se obtiene sumando los vectores-campo que produce cada una de
ellas.
La animación
adjunta aplica este
concepto para reproducir el procedimiento seguido en la
representación del campo eléctrico generado por un
sistema formado por dos cargas fijas. Antes de
manipularla recomendamos resolver el problema usando lápiz y papel.
Se han de considerar los
tres casos posibles de las cargas que producen el
campo: ambas positivas, ambas
negativas o una carga de cada signo.
Clic
aquí para descargar esta animación [Si no lo
tienes instala
Modellus 2.5 (32 bits) o
Modellus 3
(64 bits)] |
|
|
|
|
|
El dibujo de las
líneas del campo proporciona información cualitativa de cómo es la
intensidad del campo, E, en cada lugar: Es más intenso
en las regiones donde se aprietan las líneas de fuerza y más débil donde las
líneas de fuerza quedan más separadas. En consecuencia, la intensidad
del campo se relaciona con la densidad de las líneas de fuerza
que lo representan. |
|
|
|
 |
|
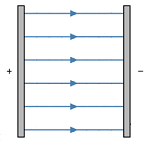
Para
muchas aplicaciones prácticas, en lugar de campos
radiales interesa disponer de
campos eléctricos uniformes y, a ser posible, de
intensidad controlable. Un dispositivo capaz de
conseguirlo es el condensador plano. Consta de dos placas metálicas enfrentadas y cargadas con la misma
carga de signo opuesto. En el espacio interior entre
ambas placas, las líneas del campo eléctrico resultan
prácticamente paralelas, indicando que el campo
eléctrico es uniforme ahí. Además, su intensidad se puede
controlar modificando el valor de la carga que
almacenan las placas, su superficie o la distancia
entre ellas. |
|
|
|
|
Además de los dos casos
vistos aquí (campo radial
y campo uniforme), cabe considerar otras muchas
distribuciones de carga que producen campos eléctricos
con
líneas de fuerza de geometría diversa (por ejemplo, un hilo conductor, una
esfera cargada, etc.). Quienes
estén interesados, pueden descargar este
documento,
donde se resuelven éstos y otros ejemplos y se aportan
conceptos útiles para ello (el concepto de flujo del campo
eléctrico y el teorema de Gauss). |
|
|
|
