| |
|
 |
LEY DE
COULOMB |
 |
|
|
|
| |
|
 |
|
El
físico e ingeniero francés
Charles-Augustin de Coulomb
(1736-1806) fue
el primero en establecer las leyes cuantitativas de la
electrostática, además de realizar muchas
investigaciones sobre magnetismo, rozamiento y
electricidad. Sus investigaciones científicas están
recogidas en siete memorias, en las que expone
teóricamente los fundamentos del magnetismo y de la
electrostática. Coulomb inventó en 1777 la balanza de
torsión para medir la fuerza de atracción o repulsión
que ejercen entre sí dos cargas
eléctricas y estableció la función que liga esta
fuerza con la distancia. Con este invento, culminado en
1785, pudo establecer la expresión matemática de la ley
que calcula la fuerza eléctrica entre dos cargas.
A la izquierda
Coulomb |
|
|
|
|
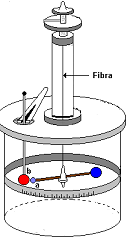
La
balanza de torsión (a la derecha de este texto) consta de una barra
que cuelga de un hilo de un material elástico como
fibra. Si la barra gira el hilo se tuerce y la fuerza de
recuperación elástica tiende a que recupere su posición
original. Para verificar la ley de Coulomb con este
dispositivo, colocamos una esferita cargada en uno de
los extremos de la barra (a) y le acercamos otra con
carga del mismo signo (b). Las esferitas se ejercen una
fuerza de repulsión eléctrica y tuercen el hilo. En
estas condiciones la fuerza de torsión que el alambre
ejerce sobre la barra es igual a la fuerza de repulsión
eléctrica entre las cargas.
Acerca
de los factores que determinan el valor de dicha fuerza,
es lógico suponer que deberá ser mayor cuanto mayor sea
la carga eléctrica acumulada por cada una de las esferas
y menor cuanto mayor sea la distancia entre ellas.
De
forma más concreta, cabe plantear que si se duplica el
valor de cualquiera de ambas cargas (q1
o q2) también se deberá duplicar el
módulo de la fuerza que se ejercen. Por tanto, la fuerza
electrostática debe ser proporcional al producto de
ambas cargas. |
|
 |
|
|
|
|
 |
|
Para
establecer el tipo de dependencia entre el módulo de la
fuerza y la distancia entre las cargas, tenemos en
cuenta que la fuerza que ejerce, por ejemplo, la carga,
q1, sobre la carga, q2,
es la misma en todos los puntos del espacio que estén a
la misma distancia de q1 y
disminuye al aumentar esa distancia, r. |
|
|
|
|
Esto equivale a
decir que la atracción o la repulsión que puede ejercer la carga
q1 sobre la carga q2 es la
misma en todos los puntos de una esfera
de superficie S = 4πr2
centrada en
q1. La fuerza disminuye al alejarnos
hacia esferas de mayor superficie y, por lo tanto, planteamos
que su módulo ha de ser inversamente proporcional a la cantidad
4πr2. |
|
|
|
Finalmente, se
ha de considerar la influencia del medio, puesto que la
interacción eléctrica no se transmite igual, por ejemplo, en el
vacío que en el aire o en el agua. A tal fin, se introduce una
constante, ε,
llamada permitividad eléctrica. La constante se escribe en el
denominador de la expresión que calcula la fuerza, con lo que un
medio con permitividad alta transmite mal la interacción
eléctrica (es un medio "no eléctrico" o dieléctrico) y un medio
con permitividad baja la transmite bien (es un medio conductor). |
|
|
|
El conjunto de
estos razonamientos conduce a la expresión operativa de la ley
de ley de Coulomb: |
|
|
|
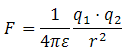 |
|
|
|
Material |
Constante (e'
) |
|
Vacío |
1 |
|
Aire
(seco) |
1,00059 |
|
Poliestireno |
2,56 |
|
Nylon |
3,4 |
|
Papel |
3,7 |
|
Cuarzo
fundido |
3,78 |
|
Vidrio
Pirex |
5,6 |
|
Caucho
de neopreno |
6,7 |
|
Agua |
80 |
|
Titanato
de estroncio |
233 |
|
|
En el Sistema
Internacional de Unidades (SI), la carga se expresa en
culombios, C, siendo la carga de un electrón igual a
1,602·10-19 C. La distancia se mide en metros,
m, y la fuerza en newtons, N. Respecto a la permitividad, ε,
resulta cómodo simplificar la ley de Coulomb, utilizando la
constante alternativa: k =1/4πε.
El mayor valor posible de esta constante, K,
corresponde al vacío (ko = 9·109 SI,
εo = 8,84·10-12
SI). Por lo tanto, en el vacío es donde la fuerza
eléctrica entre cargas tiene mayor intensidad y
cualquier medio material interpuesto produce una
disminución de la misma. Por ello, resulta
habitual usar una permitividad relativa ε' del medio, igual al
número de veces que es mayor que la del vacío
(es decir,
ε'
= ε/εo).
La tabla adjunta recoge los valores de esta
constante dieléctrica relativa en varios medios.
|
|
|
|
| |
Índice |
 |
|
|
|
|
|
|
|