| |
|
 |
ENERGÍA
Y POTENCIAL ELÉCTRICOS |
 |
|
|
|
|
Para completar la
caracterización del campo eléctrico, interesa evaluar la
energía del mismo. Asociado a ella, a su vez, se
introduce un concepto de mucha utilidad: el potencial eléctrico. |
|
|
|
|
|
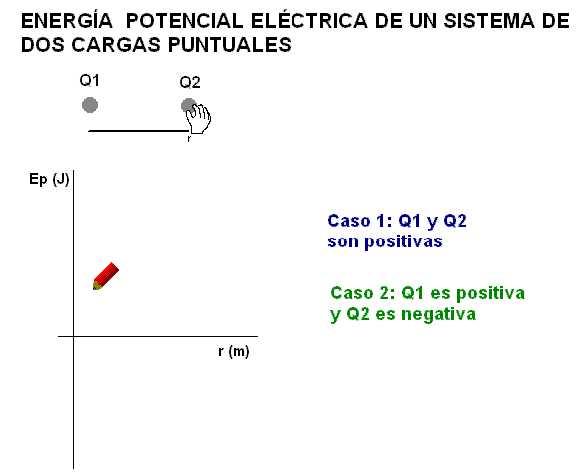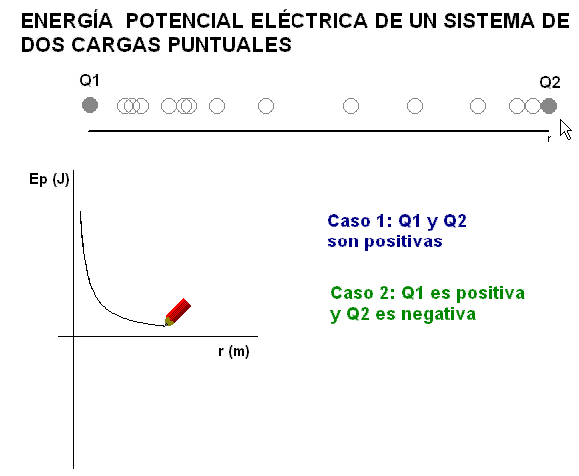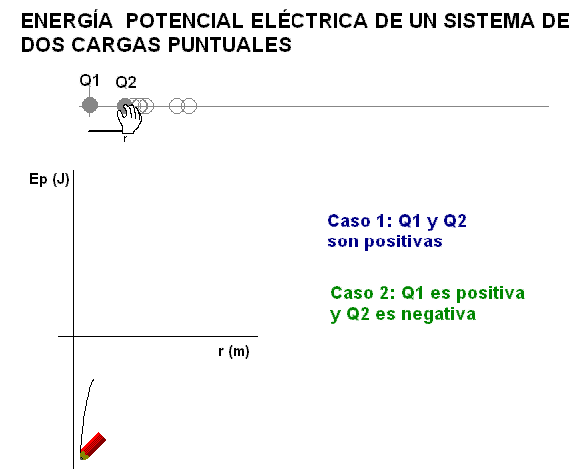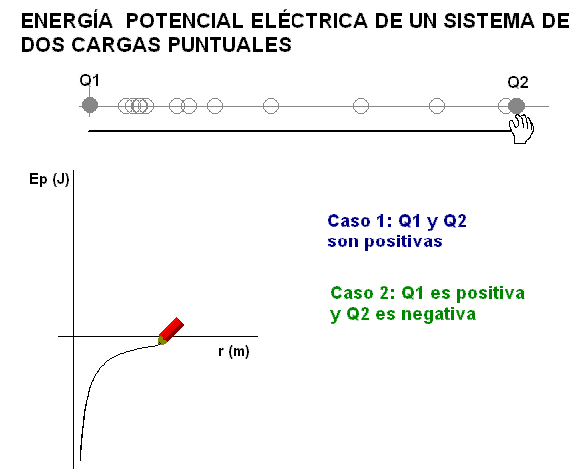
La animación adjunta calcula y representa punto a
punto la energía potencial eléctrica almacenada
por el sistema electrostático más sencillo, formado por dos cargas puntuales
en los dos casos posibles:
1) Las cargas tienen el mismo signo.
Entonces la energía eléctrica del sistema es positiva, porque,
para mantenerlo, es necesario aplicar una fuerza
externa que contrarreste a la fuerza de
repulsión eléctrica que se ejercen las cargas (Si se deja
al sistema evolucionar
libremente, dicha fuerza de repulsión eléctrica hará que las
cargas se vayan
separando y aumente su energía cinética a medida que disminuye
la energía potencial eléctrica).
2) Una carga tiene signo positivo y la otra
signo negativo. La energía eléctrica del sistema es
negativa. Para mantenerlo se precisa aplicar una fuerza externa
que contrarreste a la fuerza de atracción que se ejercen las
cargas.
Clic
aquí para descargar esta animación [Si no lo
tienes instala
Modellus 2.5 (32 bits) o
Modellus 3
(64 bits)] |
|
|
|
|
| |
|
|
|
 |
|
Cuando
tenemos un conjunto de múltiples cargas, la energía del
sistema es la suma de las energías potenciales de
interacción para cada par de ellas. Calcularla, para un
sistema ligado, equivale
a obtener la energía mínima necesaria para separar
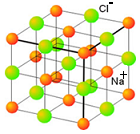
totalmente sus componentes. Esto tiene
fines útiles: Por ejemplo, permite obtener la
energía reticular de una sustancia iónica en estado
cristalino (como, por ejemplo, la sal común, formada por iones
positivos de sodio, Na+, y negativos de cloro,
Cl-), definida como la
energía que se requiere para separar totalmente las
partículas de un
mol de dicha sustancia. |
|
|
|
|
Del mismo modo que se
introduce el concepto de campo eléctrico para sustituir, o
mejor, complementar, la interpretación de las fuerzas eléctricas
entre cada dos cargas, por la idea de una perturbación que
produce en el espacio circundante a cada carga, conviene
introducir el concepto de potencial eléctrico, para
caracterizar, en relación con la energía potencial eléctrica de
un sistema, cada punto del espacio que es perturbado por una
carga. El procedimiento seguido para
obtener el valor de esta magnitud en cualquier punto alrededor
de una carga, Q, comienza también colocando ahí una
pequeña carga de prueba o carga testigo, q, positiva. Seguidamente
divide la energía potencial del sistema obtenido
(formado por ambas cargas, Q y q) entre la carga
testigo, q. |
|
|
|
|
|
|
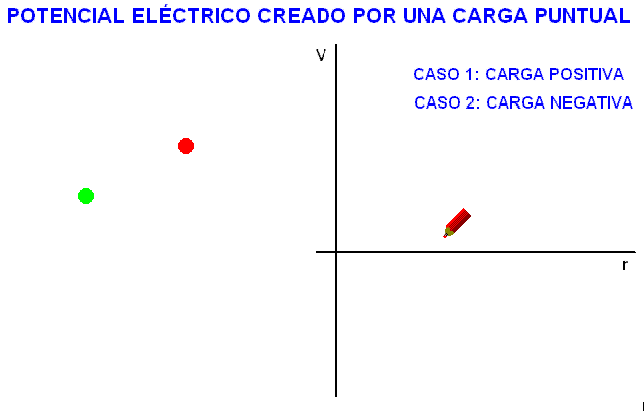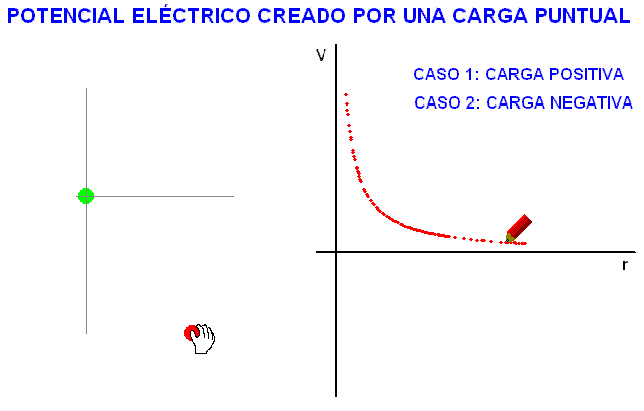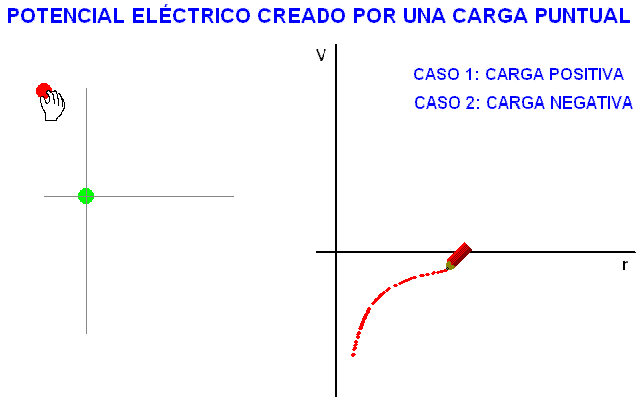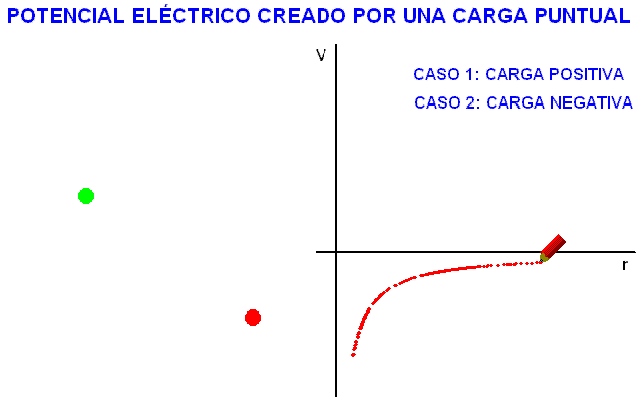
En
consecuencia, el potencial eléctrico creado por una
carga Q, a una cierta distancia, r, es:
|
| |
|
 |
| |
|
A diferencia
del campo, el potencial eléctrico es una
magnitud escalar. A semejanza de él tiene un
determinado valor en cada punto del espacio
circundante a la carga que lo produce. La
animación adjunta representa la variación de
este valor en función de la distancia a la
carga.
Clic
aquí para descargar esta animación [Si no lo
tienes instala
Modellus 2.5 (32 bits) o
Modellus 3
(64 bits)] |
|
|
|
|
