Resumimos aquí algunos aspectos del modelo mecano-cuántico, que se deriva formalmente de aplicar la ecuación ecuación de Schrödinger al átomo. En su forma más simplificada  esta ecuación se puede escribir así: HΨ = EΨ, donde el término H representa a la energía cinética y la energía potencial del sistema, Ψ es la función de onda, y E, la energía de dicho sistema.

Para cualquier valor de la energía, E, positivo, la ecuación de Schrödinger obtiene soluciones distintas de cero para Ψ. Esto implica que la probabilidad de que el sistema se encuentre en ese estado (dada por Ψ²) también es distinta de cero, lo que simplemente significa que ese sistema puede ocupar cualquier lugar del espacio y puede tener cualquier valor de la energía (siempre que no sobrepase la velocidad de la luz). Un sistema con energía, E, positiva es un sistema libre, no ligado, por ejemplo, el formado por las partículas de un gas, el constituido por un bloque de madera que se puede desplazar encima del suelo, etc.

En cambio, para cualquier valor negativo de la energía, E, la ecuación de Schrödinger sólo obtiene soluciones distintas de cero para algunos valores de E (Ψ es nula para el resto de valores). Es el caso del electrón en el átomo: Su energía potencial eléctrica (negativa) supera a su energía cinética (positiva), por lo que la energía total, E, es negativa. La solución de la ecuación de Schrödinger dicta entonces que el electrón sólo puede tener determinadas cantidades de energía. Al resolverla se obtienen todos los valores discretos de la energía y se comprueba que la función Ψ obtenida depende de cuatro parámetros, correspondientes a los números cuánticos que se introdujeron de forma poco rigurosa en el modelo de Bohr-Sommefield.

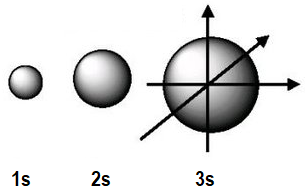
Evidentemente, en el modelo mecano-cuántico no tiene cabida el concepto de órbita electrónica ni se puede suponer al electrón una partícula localizable. En su lugar, el cuadrado de la función de ondas, Ψ², indica zonas del espacio en las que existe probabilidad de encontrar al electrón. Estas zonas reciben el nombre de nubes electrónicas u orbitales y tienen un número limitado como consecuencia del carácter ondulatorio del electrón. Cada capa sólo puede tener un número entero de ondas de De Broglie, igual que es limitado el número de ondas estacionarias que se pueden formar en una cuerda fija en sus dos extremos.

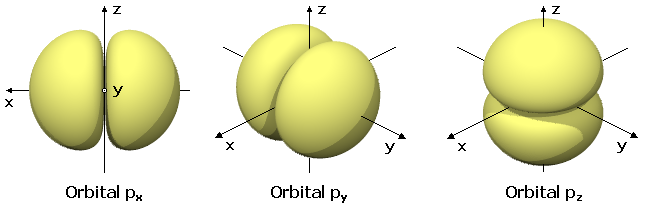
Es importante comprender que los orbitales no existen con independencia de los electrones. Allá donde hay uno o como máximo dos electrones atómicos (con espines opuestos), se obtiene una zona de probabilidad de encontrar a ese electrón o a esa pareja, cuya forma y orientación determinan los números cuánticos, l y m.

El modelo mecano-cuántico del átomo permite explicar también la diferente probabilidad que tienen distintos saltos electrónicos, ya que, tal probabilidad de que se produzcan unos u otros saltos es mayor cuanto mayor sea la superposición o la interpenetración entre los orbitales inicial y final. Por este motivo, las transiciones entre determinados orbitales son poco probables y producen líneas espectrales muy débiles, como ocurre, por ejemplo, con la transición entre dos orbitales, s, ambos con simetría esférica con centro en el núcleo. En cambio, los orbitales s y p se superponen, la transición entre ellos es más probable, y la línea espectral correspondiente es más intensa.

A propósito de estos conceptos, conviene detenerse un momento a salir al paso de una imagen distorsionada de realidad, que podríamos tener la tentación de albergar, y que consiste en imaginar a los átomos como unas entidades individuales, supuestamente aisladas, y estáticas en un determinado nivel de energía. Lo cierto es que en cualquier situación real que podamos imaginar los átomos están permanentemente interaccionando unos con otros y también con otras entidades como fotones, electrones, moléculas, etc. Por tanto, su nivel de energía oscila continuamente entre los posibles que puede tener.

Otra cuestión que no pudo explicar el modelo de Bohr y sí que explica el modelo mecánico-cuántico del átomo es el espesor de las rayas espectrales, que, en ocasiones, es muy considerable, sobre todo a elevadas temperaturas y presiones.

La imprecisión en la energía es tanto menor cuanto mayor sea el tiempo, Δt, durante el cual el electrón permanece en un cierto estado de energía (estado estacionario) ΔE -> 0, pero cuanto más rápidamente varíe la energía del electrón, mayor será la imprecisión, ΔE, que afecte a la energía y más anchas son las rayas del espectro. A temperaturas y presiones elevadas se producen de forma continuada numerosas transiciones de electrones, por tanto, las rayas del espectro son más anchas e imprecisas.

También quedó pendiente de explicar por el modelo de Bohr la existencia de direcciones privilegiadas en las uniones entre átomos, que está en el origen de la estructura y la geometría de las moléculas y/o de las redes atómicas obtenidas. A la luz de modelo mecano-cuántico, se entiende fácilmente, que las distintas orientaciones de los orbitales y las formas de enlazarse orbitales atómicos para formar orbitales moleculares están en la base de la explicación de estos hechos.

En resumen, el modelo cuántico del átomo explica de forma más y mejor fundamentada hechos que en el modelo de Bohr-Sommerfield habían necesitado de hipótesis "ad hoc" y de sucesivos y no totalmente fructíferos retoques. Pero, además, interpreta de forma satisfactoria otras muchas cuestiones que el modelo de Bohr no pudo interpretar. Adicionalmente a su carácter explicativo, el mencionado modelo cuántico del átomo enseguida mostró un impresionante carácter predictivo, pudiéndose aventurar  a su luz múltiples aspectos del comportamiento de los elementos (dependiendo de su estructura atómica), sus propiedades periódicas, las sustancias que pueden formar y sus propiedades, etc. No es una exageración decir, no sólo la química moderna, sino también, la física de materiales, la física nuclear y la física de partículas son deudoras del éxito que supuso la aplicación pionera de la teoría cuántica al átomo.