| |
|
 |
ONDAS ESTACIONARIAS |
 |
|
|
|
|
|
|
Las
ondas estacionarias son ondas producidas en un
medio limitado, como, por ejemplo, una cuerda
elástica no muy larga y fija en al menos uno de sus dos
extremos. Para generar en dicha cuerda una onda
estacionaria, se puede atar por un extremo a una pared y
hacer vibrar al otro con una pequeña amplitud. Se
obtienen pulsos transversales que viajan hasta la pared,
donde se reflejan y vuelven. La cuerda es recorrida por
dos ondas de sentido opuesto y se producen
interferencias que, en principio, dan lugar a unas
oscilaciones bastante desordenadas. |
| |
|
 |
|
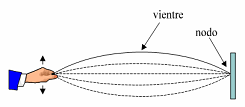
Aumentando la frecuencia con la que se agita el
extremo de la cuerda se puede conseguir que las
oscilaciones adquieran el perfil mostrado por la
figura adjunta. Corresponde a una onda en la que
aumenta sensiblemente la amplitud y tiene un
vientre fijo en el centro y dos nodos también
fijos en los extremos. Esta onda se llama
estacionaria porque, a diferencia del resto de
ondas, en las que se aprecia un avance de las
crestas y los valles, no parece moverse. |
|
|
|
|
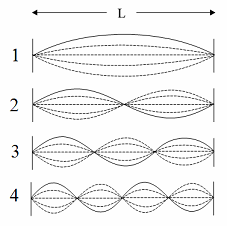
Si se
fijan los dos extremos de la cuerda y se estira
transversalmente de uno, dos, tres puntos se puede
generar en la cuerda una secuencia de ondas
estacionarias con un número creciente de nodos y
vientres, como las indicadas en la figura adjunta. |
| |
|
 |
|
Una propiedad destacada de estas ondas
estacionarias es que su longitud de onda (y,
consecuentemente, su frecuencia) no puede
adoptar cualquier valor arbitrario, sino sólo
unos determinados valores que se relacionan con
la longitud de la cuerda, mediante las
siguientes expresiones:
l1
= 2L,
l2
= 2L/2,
l3
= 2L/3,
l4
= 2L/4,...
ln
= 2nL/4 (siendo n = 1, 2,
3,..)
Teniendo en cuenta que c =
l/T
=
ln,
las frecuencias correspondientes son:
n1
=
c/2L
n2
=
2c/2L
n3
=
3c/2L
n4
= 4c/2L,.. nn
=
nc/2L
(siendo n = 1, 2, 3,..) |
|
| |
|
Estas
frecuencias se llaman
frecuencias
de resonancia
o frecuencias naturales
del medio en el que se
produce la onda (en este caso la cuerda).
A la menor
se la denomina frecuencia
fundamental
o "primer armónico" y las siguientes se designan
sucesivamente como segundo armónico, tercer armónico,
etc. En términos musicales (podemos pensar, por
ejemplo, que se trata de la
cuerda de una guitarra) al segundo
armónico se le denomina "primer sobretono", al tercero
"segundo sobretono" y así sucesivamente. |
| |
|
|
| |
|
Las ondas estacionarias tienen una
gran importancia. El viento, por ejemplo, puede producir
ondas estacionarias en un puente colgante haciendo que
la amplitud de oscilación aumente y provoque
su rotura. En general los edificios muy altos han de
proyectarse teniendo en cuenta las ondas estacionarias
que podrían tener que
soportar
y lo mismo ocurre con
los aviones. Los instrumentos de música dependen de las
ondas estacionarias para producir sonidos musicales,
desde los de cuerda (guitarra, violín,..)
a los de viento (saxofón, trompeta,..)
o de percusión. |
| |
|
El profesor Vicent Soler realizó en el IES
"Sixto Marco" de Elche un experimento muy
interesante sobre ondas estacionarias de sonido
en el interior de un tubo semiabierto.
|
| |
 |
|
 |
|
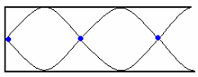
El montaje experimental utilizó un tubo de PVC
abierto en uno de sus extremos, un altavoz
conectado a un generador de ondas, un sensor de
sonido conectado al ordenador y una cinta
métrica para medir posiciones dentro del tubo.
Los estudiantes comprueban que se pueden generar
ondas estacionarias en el tubo abierto-cerrado a
una determinada frecuencia, obtienen
experimentalmente la distribución de la
intensidad por el interior del tubo e
identifican las posiciones de los nodos y los
vientres correspondientes al tercer armónico.
|
|
| |
|
Para terminar estos breves
apuntes sobre las ondas estacionarias, mostramos aquí
(con permiso del autor) varios videos Bob Barrett, que
imparte Física en la
Messiah College de Pensilvania. |
|
|
|
|
|
|
| |
|
|
|