| |
|
|
| |
|
PLANTEAMIENTO Y PROPÓSITO DEL EXPERIMENTO |
| |
|
En otros experimentos, hemos mostrado que se
puede contrastar la
hipótesis de Galileo sobre el tiro
oblicuo, mediante estudios experimentales que
comienzan con la filmación del movimiento de
objetos cotidianos que lo realizan
(concretamente, el
rebote
oblicuo de una pelotita y el lanzamiento
de un
tiro libre en un partido de baloncesto)
y siguen usando el el programa Modelllus,
para realizar análisis de la evolución de las
magnitudes que describen a dichos movimientos
filmados.
Aquí vamos a mostrar que se pueden realizar
estudios similares con el programa Tracker.
Veremos, en concreto, los análisis realizados
por profesores de Física y Química en un curso
de formación docente celebrado en 2019 en el
Cefire de Ciencias, Tecnología y Matemáticas de
Valencia. |
|
|
|
|
|
VIDEO DEL LANZAMIENTO OBLICUO |
| |
|
Para realizar los análisis sobre el tiro
oblicuo, los profesores asistentes usaron el
clip de video adjunto, que está
disponible en los fondos de la página oficial de
del programa (https://physlets.org/tracker/)
Como vemos, el montaje elaborado para realizar
esta filmación incluye la señalización de una
serie de marcas de referencia (en este caso en
dirección vertical), a partir de las cuales se
podrán determinar cuantitativamente las
posiciones de la pelotita.
|
|
|
|
|
|
|
RESULTADOS DE LOS
ANÁLISIS |
|
|
|
A
partir del análisis de las posiciones determinadas en la
imagen del video (por tanto, partiendo de los datos
experimentales), se pueden obtener con Tracker
diferentes gráficas sobre la evolución de las magnitudes
cinemáticas del movimiento filmado. El programa obtiene
la función matemática que mejor describe el movimiento
de la pelotita por ajuste de mínimos cuadrados y
permite así cuantificar las
magnitudes estudiadas. En este caso, los profesores
obtuvieron los siguientes resultados: |
|
|
|
 |
|
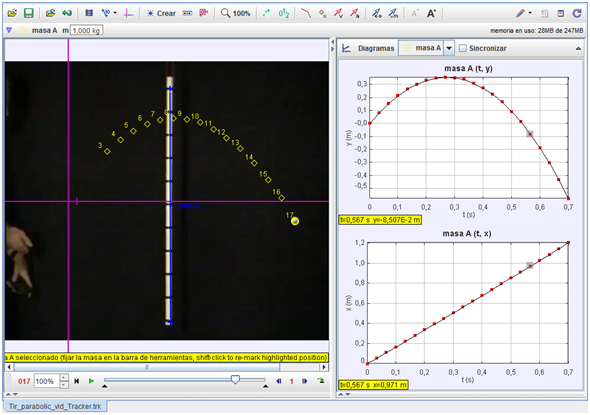
Gráficas
de las componentes de la posición
Como vemos, a la izquierda quedan señaladas posiciones
sucesivas de la pelota (un total de 17), registradas a intervalos iguales
de tiempo, y a la derecha se muestran las gráficas de
la evolución de las componentes de la posición: horizontal
(x) y vertical
(y) de la pelotita.
Evidentemente el perfil de estas gráficas es
coherente con el cumplimiento de la hipótesis de
Galileo, ya que la componente horizontal muestra
el perfil de una relación lineal (movimiento
uniforme) y la vertical muestra el perfil de una
relación cuadrática (movimiento de caída,
uniformemente acelerado) |
|
| |
|
 |
|
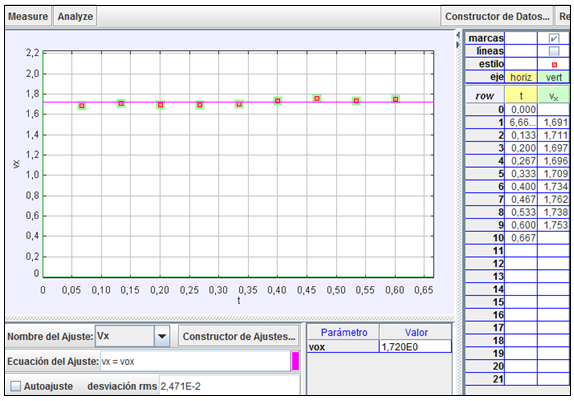
Componente
horizontal de la velocidad
Se obtiene con
total claridad el resultado de que la componente
horizontal de la velocidad es constante, como
exige la hipótesis de Galileo. El valor de dicha
velocidad horizontal constante resulta vx
= v0x
= 1,72 m/s |
|
|
|
|
 |
|
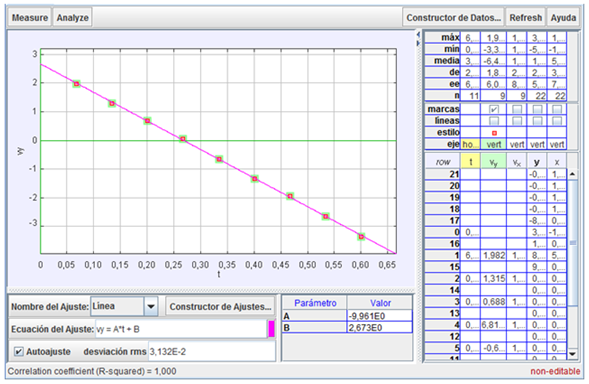
Componente
vertical de la velocidad
El mejor ajuste
para esta magnitud corresponde, como también
exige la hipótesis de Galileo, a una relación
lineal entre la velocidad vertical y el tiempo:
la ecuación de la componente vertical de la
velocidad se corresponde con la de un movimiento
uniformemente acelerado vy = A·t
+ B.
La pendiente de la gráfica representa aquí la
aceleración vertical del movimiento y viene dada
por el parámetro A. como vemos, se obtiene a =
- 9,96 m/s2, por tanto, prácticamente
igual, como así debe ser, al valor de g.
|
|
|
|
|
 |
|
Vectores
velocidad y aceleración
El programa también
permite al usuario representar los vectores que
indican la velocidad y la aceleración
instantáneas.
Esta representación muestra con
mucha claridad que la aceleración es siempre
vertical y constante, así como que el vector
velocidad es, en cada punto, tangente a la
trayectoria y que su módulo va decreciendo
mientras la pelotita se eleva y aumentando
mientras la pelotita desciende.
Clic
aquí descarga
los archivos Tracker de estos análisis |
|
|
|
|
|