RELACIÓN ENTRE EL ALCANCE Y LA ALTURA EN EL TIRO HORIZONTAL
 
 
 
 

Experimento realizado por alumnos de Bachillerato del IES "Cid Campeador" de Valencia.

  
 
 
     
 

HIPÓTESIS DE GALILEO SOBRE EL TIRO HORIZONTAL
 

Una de las mayores aportaciones de Galileo fue determinar la trayectoria parabólica de los proyectiles a partir de la composición de dos movimientos teóricos, que supuso independientes entre sí. En la obra "Diálogos sobre los dos grandes sistemas del mundo, ptolemaico y copernicano" (1632) formuló la siguiente hipótesis: "Sabemos que el movimiento que tendrá lugar sobre un plano será uniforme y perpetuo, en el supuesto de que el plano se prolongue hasta el infinito. Si por el contrario, el plano es limitado, el móvil que suponemos dotado de gravedad, una vez llegue el extremo del plano y continúe su marcha, añadirá al movimiento precedente, uniforme e inagotable, esta tendencia hacia abajo, debida a la gravedad. Nace así un movimiento descendente naturalmente acelerado. Pues bien, a este tipo de movimiento yo le llamo proyección y hemos de demostrar alguna de sus propiedades, la primera de las cuales es la siguiente proposición: Un proyectil que se desplaza con un movimiento compuesto por un movimiento horizontal y uniforme y por un movimiento descendente naturalmente acelerado, describe, en este movimiento, una línea semi-parabólica"

 .

 

DERIVACIÓN DE LA HIPÓTESIS DE GALILEO. PLANTEAMIENTO Y PROPÓSITO DEL EXPERIMENTO
 

La hipótesis de Galileo sobre el lanzamiento de proyectiles, aplicada al tiro horizontal, permite escribir sendas ecuaciones de los movimientos horizontal y vertical. Partiendo de dichas ecuaciones, se deduce la siguiente expresión que relaciona los posibles alcances, A, con las alturas, h, para cada velocidad horizontal de lanzamiento, v0:

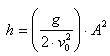
Esta relación es una clara consecuencia contrastable de la hipótesis de Galileo, por lo que su confirmación experimental, que nos proponemos en este experimento, equivale a confirmar dicha hipótesis.

 

DISEÑO EXPERIMENTAL
 

Se trata de realizar diferentes lanzamientos horizontales de una bolita o una pelotita desde varias alturas (todos con la misma velocidad inicial) y, después de medir los correspondientes alcances, comprobar si el cociente entre h y A2 es constante.

 

Para que la velocidad horizontal inicial del lanzamiento sea siempre la misma se utilizará un plano inclinado o rampa desde la que se soltará la bolita colocándola de inicio siempre en la misma posición. Dicha rampa se fijará sobre una plataforma horizontal siempre en el mismo lugar. Si en el laboratorio se dispone de puertas lógicas, se usarán para cuantificar también la velocidad inicial de los lanzamientos.

 

 

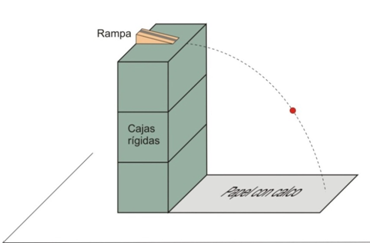Para conseguir una altura variable, se puede desplazar la plataforma mediante un soporte vertical de los que existen en los labora-torios escolares. También cabe utilizar varios objetos como, por ejemplo, cajas rígidas del mismo tamaño, e irlas apilando unas sobre otras. Otra posibilidad es mantener fija la altura de la plataforma de lanzamiento e ir cambiando la altura de otra plataforma preparada para recibir el impacto de la bolita.

Finalmente, para medir los alcances, se puede usar un papel de calco sobre un papel blanco o milimetrado colocándolo en la bandeja de llagada. También se puede echar en dicha bandeja una capa fina de arena, con el fin que la bola deje, al impactar sobre ella, una marca nítida. Una tercera opción es pintar la bolita con tiza para que cuando choque contra el suelo deje una marca.
 

En general, convendrá realizar cada lanzamiento (desde una determinada altura) varias veces y, en el caso de que las señales de impacto de la bolita se encuentren en puntos distintos, tomaremos como valor más representativo del alcance el valor medio.

 

RESULTADOS
 

En la fotografía adjunta se observan algunos de los detalles principales del montaje experimental. Los estudiantes colocaron dos puertas lógicas en el carril horizontal (en la fotografía adjunta puede verse la segunda de ellas al final del carril) y usaron un papel blanco y otro de calco para determinar el punto de impacto. Para conseguir diversas alturas del tiro horizontal, modificaron la que correspondía a la superficie donde se producía el impacto, utilizando algunas cajas y taburetes del laboratorio.

  

 

 

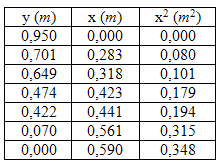
Con los valores obtenidos confeccionaron la siguiente tabla de datos adjunta sobre las alturas, y, los correspondientes alcances, x, y los cuadrados de ellos, x2.

Puesto que, para que se cumpla la hipótesis de Galileo, la representación de y = f(x) ha de producir una parábola invertida, mientras que la de y = f(x2) ha de producir una recta descendente, los estudiantes construyeron ambas gráficas usando una hoja de cálculo. Como se observa a continuación, ambas gráficas cumplieron sobradamente estas expectativas, confirmando claramente esta derivación de la hipótesis de Galileo.

 

 

 
Teniendo en cuenta, por otra parte, que la pendiente de la recta y=f(x) ha de ser:
 

 
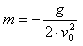Se puede usar su valor para calcular la velocidad inicial, v0, del lanzamiento. Si se acepta que g sea igual a 9’8 m/s2, se obtiene:
 

 

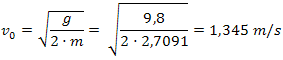Los alumnos compararon este valor con el obtenido en el mismo experimento en el plano horizontal usando las puertas lógicas, que fue igual a 1.386 m/s. Como vemos, ambos valores resultaron muy próximos (la desviación entre ellos es del orden del 3%).