Modelo de visión de Kepler

MODELO DE VISIÓN DE KEPLER - 1

En 1604 Kepler (1571-1630) publicó el libro Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur que estaba dividido en once capítulos, los cinco primeros dedicados a cuestiones de óptica y los restantes a temas de astronomía. Aunque Kepler es mucho más reconocido por sus aportaciones en astronomía, también hizo contribuciones muy importantes en óptica: Enunció una primera aproximación satisfactoria de la ley de la refracción, distinguió claramente entre los problemas físicos de la visión y sus aspectos fisiológicos, y analizó cuidadosamente el aspecto geométrico de diversos sistemas ópticos.

Kepler conocía un antiguo problema, que ya había planteado Aristóteles y al que no se había dado solución: ¿por qué los rayos de Sol percibidos durante un eclipse a través de los dedos entrecruzados o entre las hojas de los árboles dibujan lúnulas sobre el suelo?. Las lúnulas son imágenes de la Luna que se producen cuando la luz solar atraviesa pequeñas rendija que dejan las hojas o nuestros dedos. El proceso de formación de estas imágenes es similar al que forma las imágenes en una cámara oscura. Trasladado a ella el problema, nos deberíamos preguntar por qué la forma del agujero por donde entra la luz no influye en la forma de la imagen del objeto que se ve en la pantalla. La teoría de Alhacen no resolvía esta cuestión.

Fotografía tomada en Valencia de lúnulas observadas en la sombra de un árbol durante el eclipse de Sol del 3-10-2005.

El problema se hizo muy evidente cuando, durante un eclipse de Sol que tuvo lugar en el año 1600, Kepler observó que el diámetro del disco lunar medido en una cámara oscura durante el eclipse era ¡menor que cuando se medía el mismo diámetro en fase de Luna llena!. El astrónomo Tycho Brahe (1546-1601), también se había apercibido del hecho y ante las dificultades de encontrar una explicación óptica, llegó a formular una hipótesis de dilatación periódica de la Luna. Porque, si tal como planteaba el modelo de Alhazen, en la cámara oscura entrara para formar la imagen un único rayo procedente desde cada punto del disco solar, no se podría justificar la variación del diámetro lunar que se observa en la pantalla de este dispositivo.

Para afrontar estas dificultades Kepler planteó un nuevo modelo de formación de imágenes. El primer aspecto novedoso de su propuesta fue considerar a la luz emitida por cada punto del objeto como una esfera en expansión y a los rayos solamente como elementos direccionales ideales, sin entidad real. Escribió: El rayo de luz no es nada de la misma luz que marcha.

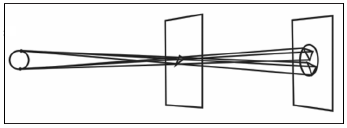
De acuerdo con la propuesta de Kepler, cuando una parte del haz esférico emitido por la fuente puntual entra en el orificio de la cámara oscura, se selecciona un haz divergente de luz y se obtiene en la pantalla una mancha luminosa con la misma forma de la hendidura, por ejemplo triangular. Como, para una fuente luminosa extensa y lejana, se trazan multitud de haces divergentes desde cada uno de sus puntos, la superposición de las pequeñas manchas triangulares compone en la pantalla una réplica de la fuente luminosa, es decir, una figura que tiene la misma forma que ella.

Además de explicar la obtención de réplicas de las fuentes luminosas que se observan en la cámara oscura, la hipótesis geométrica que planteó Kepler sobre la propagación de la luz también resuelve el problema de la dilatación del disco lunar que se observa en dicha cámara durante el eclipse solar.

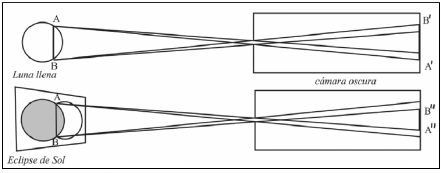
En la figura adjunta se señala una cuerda, AB, sobre el disco lunar en fase de Luna llena. Trazando haces de luz desde sus extremos, se obtiene en la pantalla de la cámara oscura una cuerda de tamaño A’B’ en el círculo luminoso (figura superior). Ahora bien, durante un eclipse de Sol, la cuerda lunar AB no es una fuente luminosa y los puntos A y B son fuentes puntuales del Sol que limitan con esa cuerda. Las manchas luminosas obtenidas sobre la pantalla de la cámara oscura tienen cierto tamaño y, por eso, la medida de la cuerda del círculo negro, A’’B’’ (figura inferior), es más pequeña que en el caso de Luna llena.

Índice