| |
|
 |
OTROS
EJEMPLOS DE DESCOMPOSICIÓN DE
MOVIMIENTOS |
 |
|
|
|
|
| |
|
|
| |
El procedimiento
que utilizó Galileo para estudiar los movimientos de
proyectiles, consistente en descomponer movimientos complejos en
otros más simples, y la posibilidad inversa de obtener
movimientos complicados mediante la composición de otros más
sencillos resulta de gran utilidad en otras muchas situaciones.
|
|
| |
|
|
| |
|
 |
|
Por
ejemplo, la animación adjunta resuelve el problema de
encontrar la posición a la que llega una canoa que cruza un río, suponiendo que dicho movimiento se puede
obtener como resultado de la composición del movimiento
horizontal de la corriente (uniforme) y el movimiento
vertical de la canoa (supuesto también uniforme).
La
animación permite modificar en cualquier momento los
parámetros del problema (velocidad de la corriente, velocidad de la canoa
y ángulo inicial).
Clic
aquí para descargar un documento textual en el que
se resuelve este problema, planteado como investigación.
Clic
aquí
para descargar la animación Para manipularla en tu
ordenador, descrarga
Modellus |
|
|
| |
|
|
| |
|
 |
|
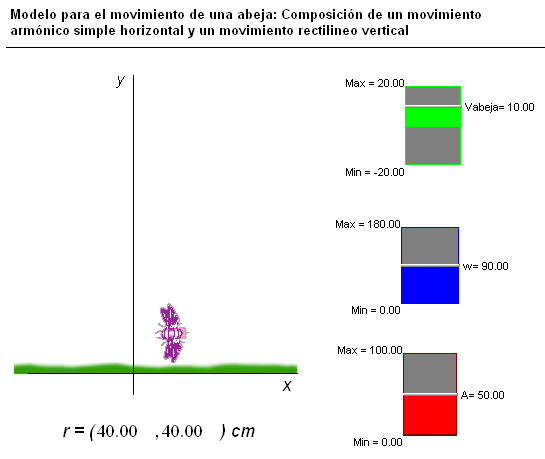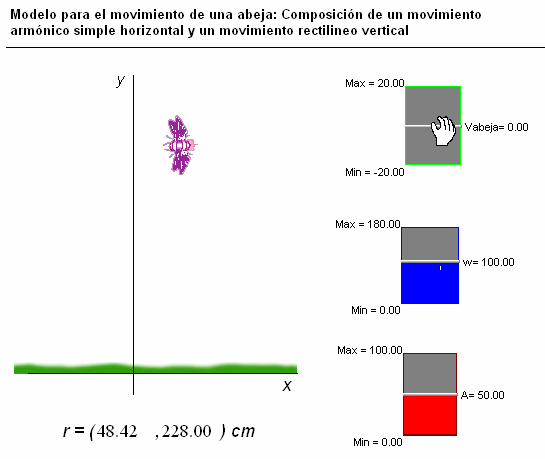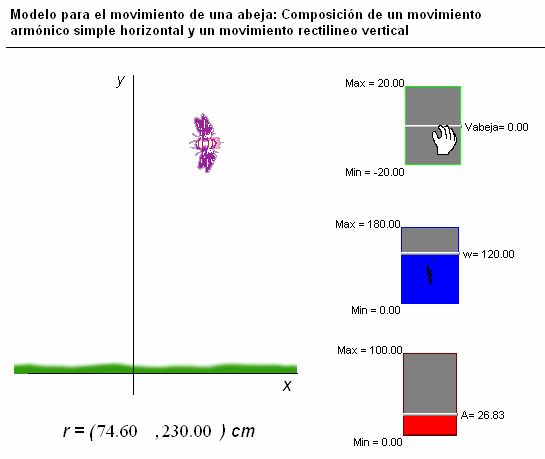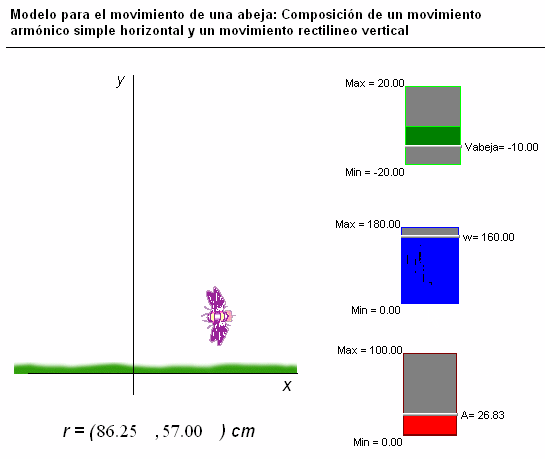
Otro
ejemplo, que muestra esta otra animación, es el del movimiento
de este insecto (a la derecha), que, en este caso, se
ha simulado mediante
la composición de un movimiento de zigzag u oscilación horizontal
(armónico simple) y un movimiento de traslación
vertical (uniforme).
Usando
los controladores manuales que hemos colocado en la
pantalla, se puede modificar la frecuencia y la amplitud de la
oscilación, así como el sentido y la velocidad del
movimiento de traslación vertical.
Clic
aquí
para descargar la animación. Para manipularla en tu
ordenador, descarga
Modellus
|
|
|
| |
|
|
| |
Una
aplicación particularmente interesante de la composición de movimientos
es la que resulta al sumar dos movimientos de
oscilación perpendiculares. Si dichos movimientos son
armónicos simples y los valores de sus frecuencias guardan entre
sí una relación numérica sencilla (1/2, 2/3,..) el movimiento
resultante dibuja trayectorias cerradas y simétricas. En el tema
dedicado al estudio de los movimientos
de oscilación se puede descargar una
animación, que
genera estas trayectorias, llamadas
figuras
de Lissajous. |
|
| |
|
|
| |
| |
Índice |
 |
|
|
|
| |
|
|
|

