ECUACIÓN DEL MOVIMIENTO ONDULATORIO

 
La ecuación del movimiento ondulatorio proporciona en cada instante el valor de la elongación (yP ) de un punto cualquiera del medio que transmite la onda.
 

 

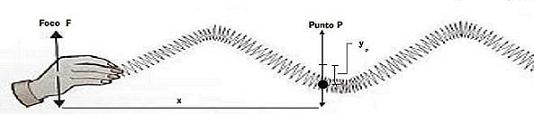
Para obtenerla situamos ese punto arbitrario, P, a una cierta distancia, x, del foco de la onda, F, y llamamos fF(t) a la ley rige la evolución del movimiento de dicho foco. Una ecuación que proporcione en cada instante la elongación del punto P ha de reflejar el hecho de que P repite el movimiento del foco con un cierto retardo de tiempo, t' , igual al tiempo que tarda la perturbación en viajar desde el foco, F, al punto, P.
 
Si c  es la velocidad de propagación de la onda, el retardo t' es t' = x/c , con lo que escribimos de forma genérica la siguiente función de onda:
 

f  (x, t) = f (t - x/c)   para una onda que se propaga de izquierda a derecha

    f (x, t) = f (t +x/c)   para una onda que se propaga de derecha a izquierda
 

Dentro de este planteamiento general, consideramos el caso de una onda armónica en la que el foco tiene un movimiento armónico simple, de ecuación fF(t) = A sen w·t , y la vibración se transmite desde cada punto al siguiente sin pérdida de energía. Entonces, la ecuación del movimiento ondulatorio es f (x, t) = A sen w (t - x/c), aunque teniendo en cuenta cómo se relacionan las magnitudes del movimiento ondulatorio (c, T, w , l , n) es más útil escribirla así:

f (x, t) = A sen 2p (t /T - x/l)
 
Esta forma de expresar su ecuación destaca el hecho de que el movimiento ondulatorio tiene una doble periodicidad: en el espacio y en el tiempo.
 
Para observar la periodicidad espacial, damos un valor fijo al tiempo, t, lo que equivale a tomar una foto del medio en un instante. En ese instante, las elongaciones de dos puntos vibrantes, a distancias x1 y x2 del foco, se diferencian por un desfase espacial Fx =2p (x2 - x1) / l.
 

 

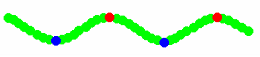
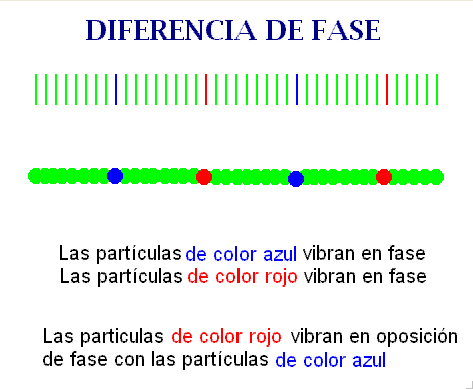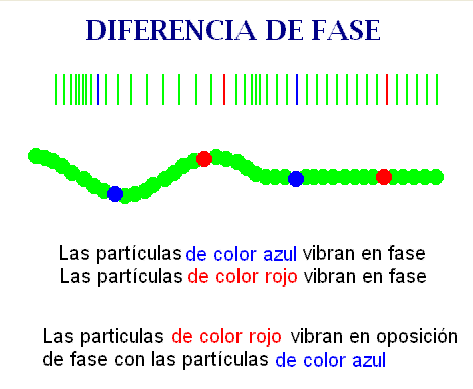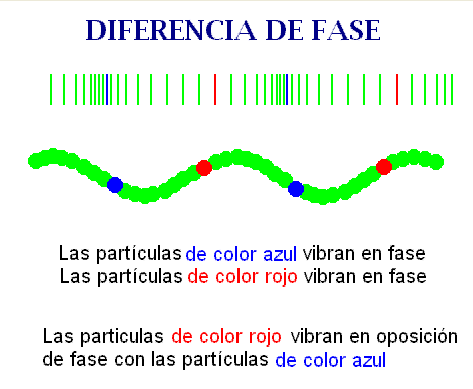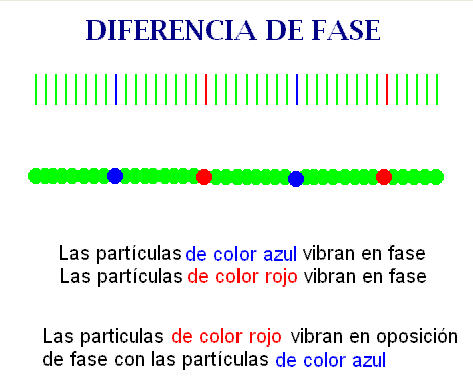
Cuando la separación entre esos dos puntos resulta x2 -x 1 = n·l (n = 0, 1, 2,..) el desfase espacial Fx  es un múltiplo entero de 2p, por lo que la elongación de ambos puntos es siempre igual y vibran acompasadamente o en concordancia de fase. Así lo hacen por una parte las partículas rojas y por otra las partículas azules de la figura adjunta. Si esa distancia es x2 - x 1 = (2n+1)·l/2, el desfase espacial entre los puntos es un múltiplo impar de p y vibran en oposición de fase, como lo hacen las partículas partículas rojas con respecto a las partículas azules.
 
Razonamos de forma similar para observar la periodicidad temporal del movimiento ondulatorio. En este caso, fijamos un punto del medio, x , lo que equivale a filmar el movimiento de oscilación de ese punto. Su elongación en dos instantes diferentes t1 y t2  se diferencia por un desfase temporal, Ft =2p (t2 - t1) / T
 

 

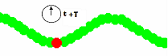
Cuando el intervalo de tiempo entre ambos instantes es t2 - t1 = n·T (n = 0, 1, 2,..), el desfase temporal Ft  es un múltiplo entero de 2p, y el punto tiene en ambos instantes en el mismo estado de vibración, como ocurre con la partícula roja en las instantáneas primera y tercera de la izquierda [tomadas en un cierto instante, t , y un periodo después (t +T)]

El caso opuesto ocurre cuando el intervalo de tiempo entre ambas instantáneas es t2 - t1 =(2n+1)T /2. Entonces, el desfase temporal es un múltiplo impar de p y la partícula se encuentra en dos estados de vibración opuestos, como ocurre con la partícula roja al comparar su situación en la figura segunda [correspondiente a una instantánea tomada en el instante (t +T/2) ] con las otras dos.

 

 
 

Para reforzar estos conceptos hemos elaborado una animación Modellus interactiva.

Se representa una onda longitudinal y otra transversal y se destacan algunas partículas, cuyos estados de vibración relativos tienen lugar en concordancia de fase y en oposición de fase.

El usuario puede colocar el cursor encima de otras partículas y editarlas, lo que le permitirá colorearlas a voluntad y comprobar comparativamente sus estados de vibración.

Clic aquí para descargar esta animación [Si no lo tienes instala Modellus 2.5 (32 bits) o Modellus 3 (64 bits)]