| |
|
 |
MAGNITUDES QUE DESCRIBEN UNA ONDA ARMÓNICA |
 |
|
|
|
|
|
|
El movimiento de
vibración más sencillo posible es el
movimiento armónico simple.
Si generamos este tipo de movimiento en un punto de un medio
elástico (por ejemplo un resorte), ese punto actúa como foco de una onda armónica. |
|
|
|
 |
|
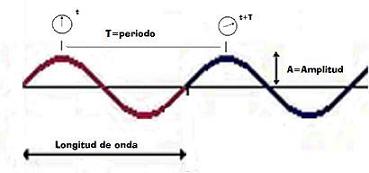
En la figura
situada a la izquierda de este texto, se representa una onda armónica transversal
producida en un muelle. Es como si se hubiera
hecho una fotografía en un cierto instante, mientras
todos los puntos del muelle están realizando un
movimiento armónico simple perpendicular a la dirección
de propagación. Entonces, se producen
alternativamente una serie de "crestas" y de "valles". |
|
|
|
|
Para describir a la
onda armónica, se requieren las siguientes
magnitudes: |
|
|
|
La longitud de onda,
λ, que es igual
a la distancia entre los centros de dos
crestas consecutivas (o entre dos vallesconsecutivos) |
| |
|
El periodo,
T,
es el tiempo que tarda la perturbación en
avanzar una longitud de onda. |
|
|
|
La velocidad de
propagación de la onda, c, que es la rapidez con la
que avanza la perturbación. |
| |
|
Entre estas
tres magnitudes se cumple la siguiente relación
fundamental: c = λ/T |
|
|
 |
|
|
|
|
Fijándonos en el
movimiento de oscilación de cada partícula que va siendo
alcanzada por la onda, añadimos las siguientes magnitudes:
La amplitud,
A, máxima separación que alcanza cada partícula vibrante respecto de su posición de equilibrio
El periodo, T, tiempo que se tarda en realizar cada oscilación
(coincide con el periodo de la onda, puesto que, mientras una
partícula completa una oscilación, la vibración se transmite una
distancia igual a la longitud de onda)
La frecuencia, ν, número
de oscilaciones que realiza cada partícula por unidad de tiempo
La
pulsación, w, que es equivalente a la frecuencia de oscilación
de cada partícula, ν, pero expresada en radianes por segundo (una oscilación corresponde
a 2π radianes)
|
|
|
|
|
|
|
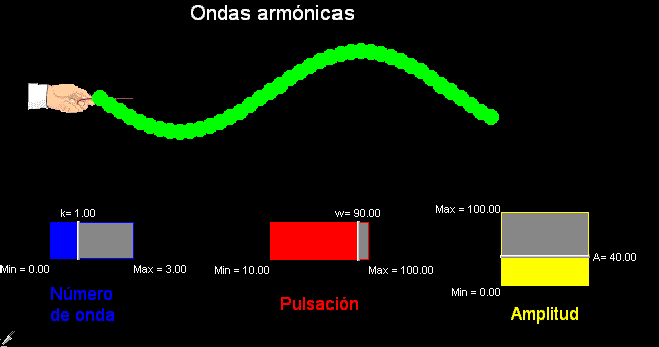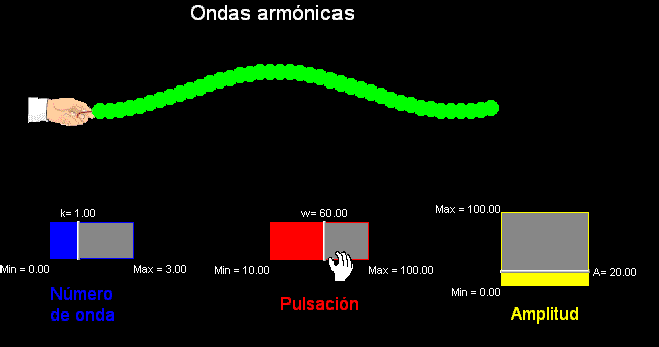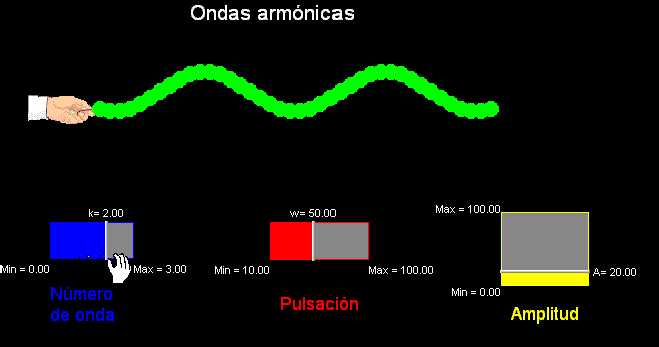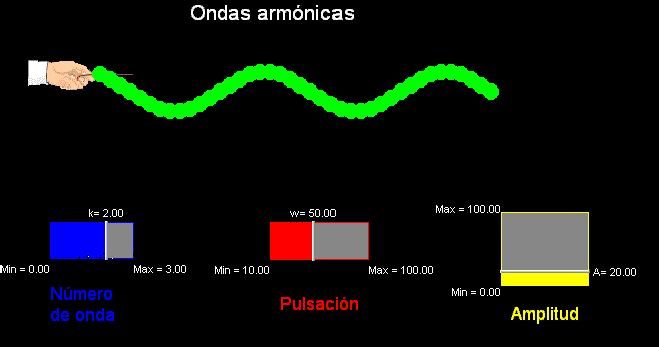
Para
practicar con el manejo de todas estas magnitudes que caracterizan
al movimiento ondulatorio puede usarse la animación
Modellus adjunta, en la que se
simula el
movimiento de una cuerda a la que se hace vibrar desde un
extremo.
Se puede modificar
directamente desde la pantalla la amplitud, A, la pulsación,
w, y el número de ondas
k (k es inversamente proporcional a la longitud de onda,
según la relación k = 2π/λ),
comprobando el
efecto que tiene cada modificación sobre la onda y sobre el resto
de magnitudes que la describen.
Entrando en la venta de
condiciones iniciales, se puede modificar
cualquiera del resto de magnitudes que describen
este movimiento ondulatorio.
Clic
aquí para
descargar esta animación. Para usarla en tu ordenador, descarga
Modellus |
|
|
|
|
|
La imagen animada adjunta
procede de una
aplicación en lenguaje Flash (ya no disponible), que era
interactiva.
Como se ve, simula un generador
de pulsos y ondas en una cuerda, pudiendo modificar diversos parámetros: la
tensión de la cuerda, la frecuencia, la amplitud del
pulso o de la onda, y, también, la naturaleza del
extremo opuesto al foco, que puede ser un punto con
libertad de movimiento en la dirección de las
vibraciones, un punto fijo o un punto más de una cuerda
que tendría una longitud.
Puesto que el lenguaje Flash
dejó de ser operativo en Internet y, en
consecuencia, las aplicaciones construidas con este
lenguaje, ya no se pueden utilizar online, filmamos la
secuencia que aquí se muestra, en la vemos como, al ir modificando
parámetros que caracterizan al movimiento ondulatorio,
se pueden visualizar diversas
propiedades de la onda o el pulso generados.
|
|
 |
|
|
| |
Índice |
 |
|
|
|
|
|
|