| |
|
 |
ECUACIONES
DE LOS MOVIMIENTOS |
 |
|
|
|
|
|
|
Con un buen
manejo de las tres magnitudes cinemáticas (posición,
velocidad y aceleración) se pueden describir con precisión
los movimientos (carácter explicativo de la teoría). La cinemática aspira
además a dotarse de un carácter
predictivo, es decir, a prever la evolución (posterior y
también anterior) de un movimiento, si en un instante
determinado se conocen sus propiedades y se le puede
caracterizar como un movimiento de un tipo determinado
(por ejemplo, uniforme, uniformemente acelerado,
armónico,..). A este propósito sirven las ecuaciones de
los movimientos. |
| |
|
Para escribir las
ecuaciones de un movimiento se requiere conocer la
expresión de la evolución de su aceleración
(o, si ésta es constante, su valor).
Además es preciso saber en un instante determinado la
posición que ocupa el móvil y su velocidad. Con estos
datos, el movimiento está completamente definido. Como
la aceleración es la derivada de la velocidad, anti-derivando
la aceleración se obtiene una colección de ecuaciones
que pueden representar a la velocidad. De todas ellas,
la ecuación de la velocidad de cada movimiento concreto
es aquella que se verifica para el valor que se conoce
de la velocidad en un instante determinado. El mismo
proceso permite obtener la ecuación de la posición, si
se conoce la de la velocidad. |
|
|
|
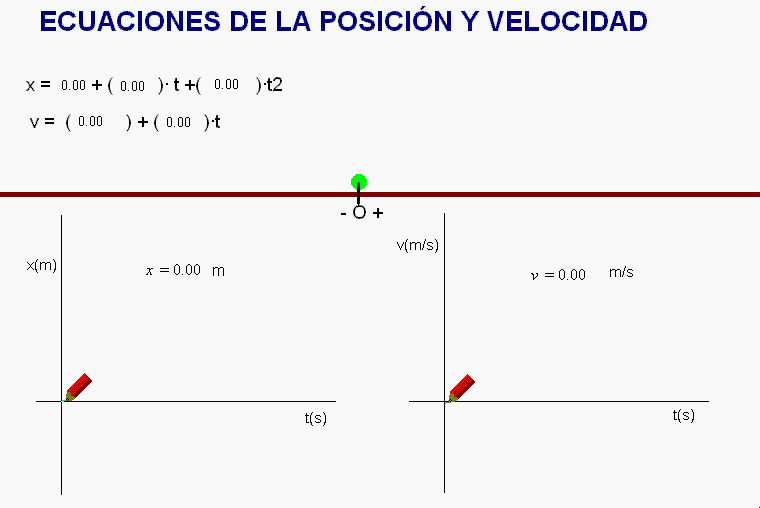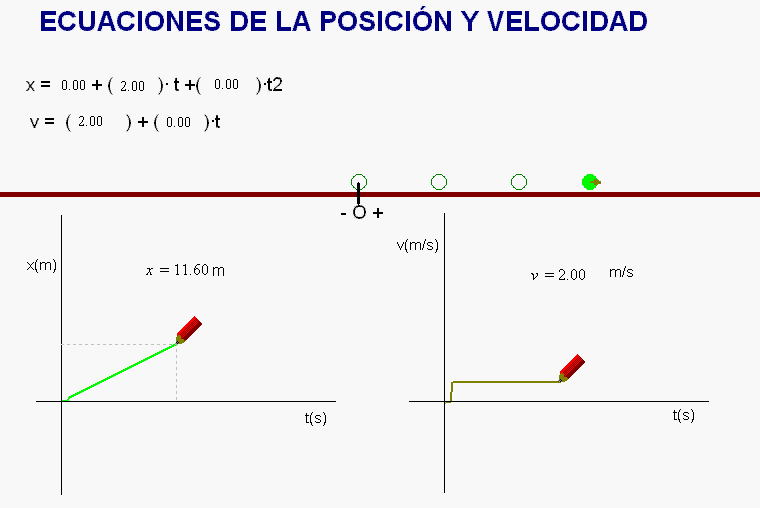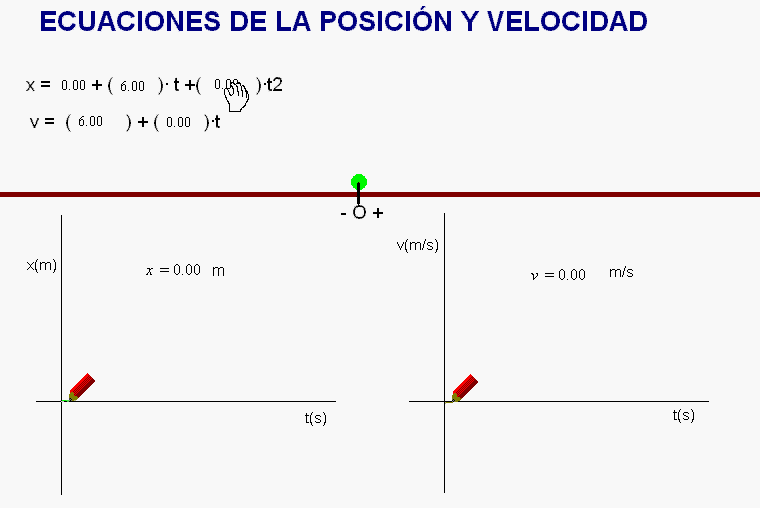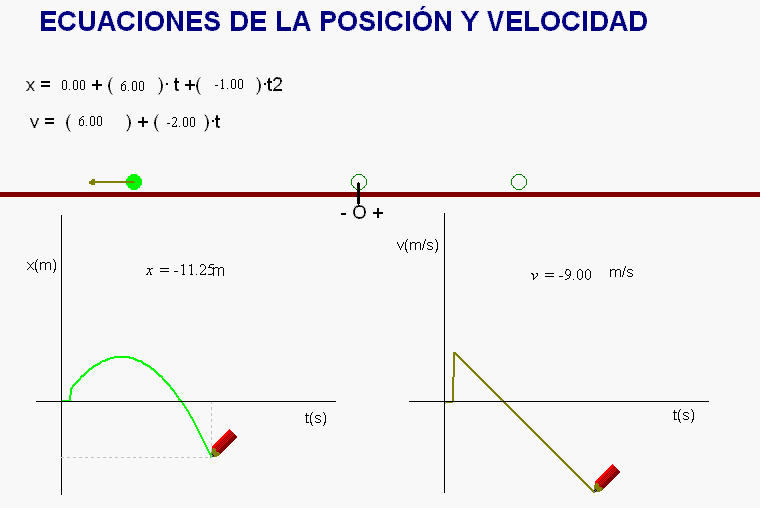
Usando la animación
adjunta, se pueden incorporar parámetros
(posición inicial, rapidez inicial, aceleración)
en las ecuaciones de un movimiento rectilíneo,
el cual, sobre su trayectoria, puede ser
uniforme (velocidad constante) o uniformemente
acelerado (aceleración tangencial constante).
Una
vez lo hemos hecho, la animación completa las
ecuaciones del movimiento de que se trate, lo
simula, y va dibujando gráficas de la evolución
de la posición y de la velocidad.
Clic aquí
para
descargar la animación [Si no lo tienes instala
Modellus] |
|
 |
|
|
|
| |
Índice |
 |
|
|
|
|
|
|
|
|