|
 |
MAGNITUDES CINEMÁTICAS - Velocidad y aceleración |
 |
|
|
|
| |
|
Además de indicar
posibles cambios en la posición de un movimiento,
interesa dar lo rápido que se producen estos cambios
de posición. Se pueden definir tantas maneras de
expresar este concepto como formas de dar los cambios de
posición. Así, se define una rapidez sobre la trayectoria
(cociente entre el cambio de posición sobre la
trayectoria y el intervalo de tiempo correspondiente),
un vector velocidad (cociente entre el vector
desplazamiento y el intervalo de tiempo), una velocidad
angular (cociente entre el cambio de posición angular y
el intervalo de tiempo), etc. |
| |
|
Para todos estos
conceptos se ha de distinguir entre el valor medio,
correspondiente a un determinado trayecto, y el valor
instantáneo de
la magnitud. Piénsese, por ejemplo, en una
persona que realiza un viaje de 30 km y
tarda 30 minutos. Días después recibe la notificación de
una multa por "exceso de velocidad", detectada por un radar.
Aunque el límite de velocidad en esa carretera pudo ser 120 km/h no podrá usar el concepto de rapidez media para
recurrir la multa. El valor medio de su rapidez sobre la
trayectoria es
60 km/h, (30 km / 0,5 horas) pero seguramente el radar detectó una rapidez instantánea
mucho mayor. |
| |
|
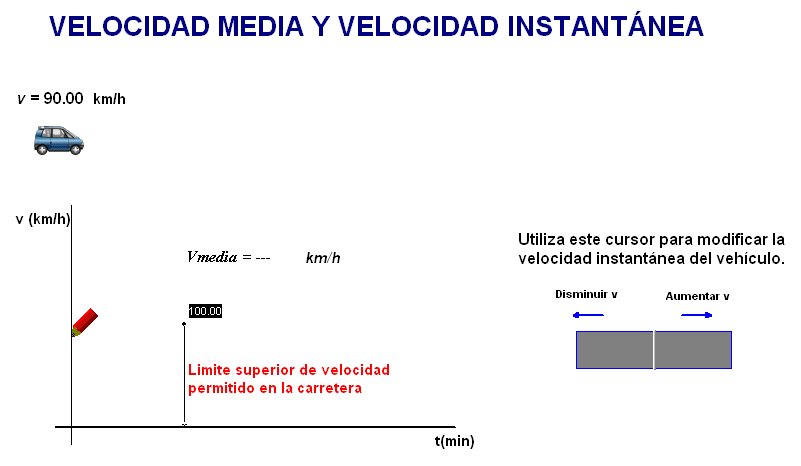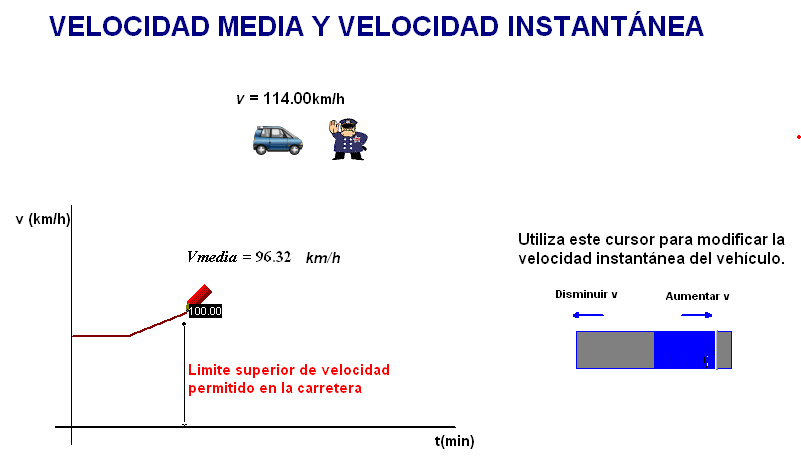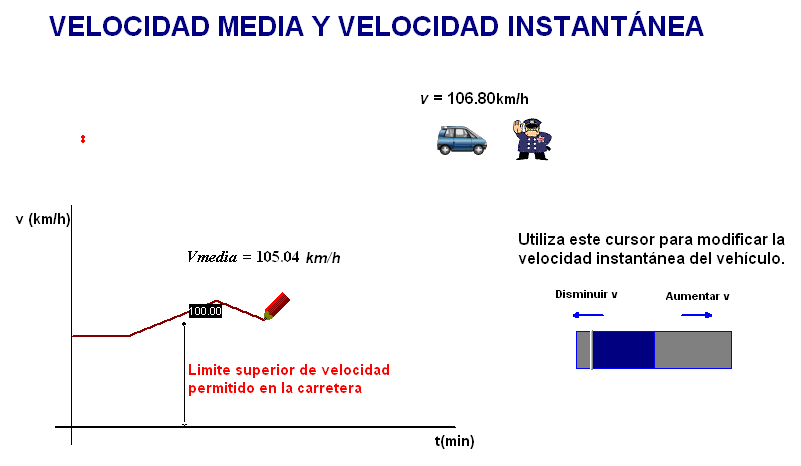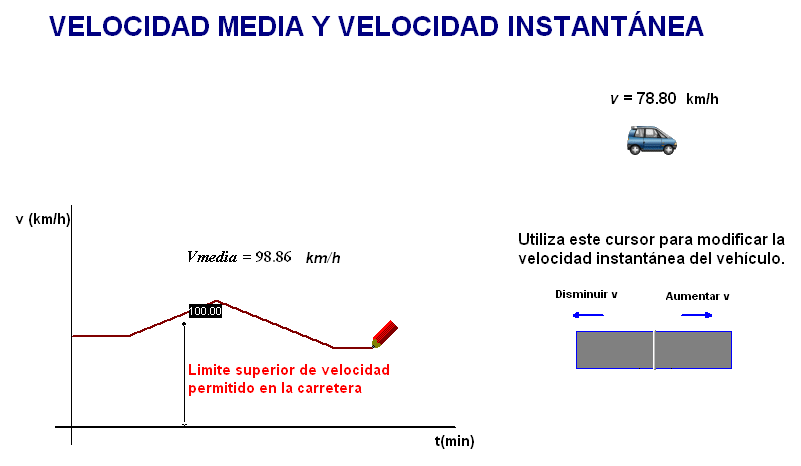
Con la animación
adjunta (debajo) se pueden simular diferentes movimientos en una
carretera con límite de velocidad de 100 km/h,
y comprobar que se puede superar perfectamente el
límite y tener una rapidez media bastante inferior. |
| |
|
 |
|
Clic
aquí para
descargar la animación [Si no lo tienes instala
Modellus] |
| |
|
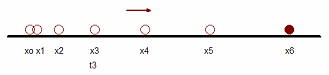
El valor instantáneo
de la rapidez es el que interesa. Para entrever su
definición pensamos en un movimiento cada vez más
rápido, como el que se representa cualitativamente en la
figura adjunta (abajo). Nos proponemos encontrar un
procedimiento para obtener la rapidez en un instante
preciso, en este ejemplo, el instante indicado en el
dibujo como t3 (correspondiente a la posición
x3) |
| |
|
 |
|
La
fórmula de la rapidez media (cambio de posición dividido
entre intervalo de tiempo) permite calcularla en cualquier intervalo de tiempo
que se inicie en t3.
Como el movimiento es cada vez más rápido, la rapidez
media es mayor cuanto más tiempo dejemos transcurrir
desde ese instante, t3. Los valores de esa
rapidez media son todos mayores que el instantáneo al
pasar por la posición x3, pero, si se
consideran intervalos de tiempo cada vez más cortos (con
origen t3), esos valores cada vez son más
próximos al valor de la
rapidez en dicho instante, t3.
|
| |
|
Teniendo en
cuenta esta disquisición, la rapidez instantánea en un
cierto instante t se
define como
el valor límite al que tienden los valores de la
rapidez media, cuando se hace tender el intervalo de
tiempo (medido desde t) a cero. Obtener este límite
equivale matemáticamente a obtener la derivada de la
función que representa la evolución de la posición
a lo largo del tiempo. Teniendo en cuenta la
interpretación geométrica del concepto de derivada, dicha derivada se puede
calcular
determinando en el instante considerado la pendiente de
la tangente a la gráfica posición-tiempo. |
| |
|
 |
|
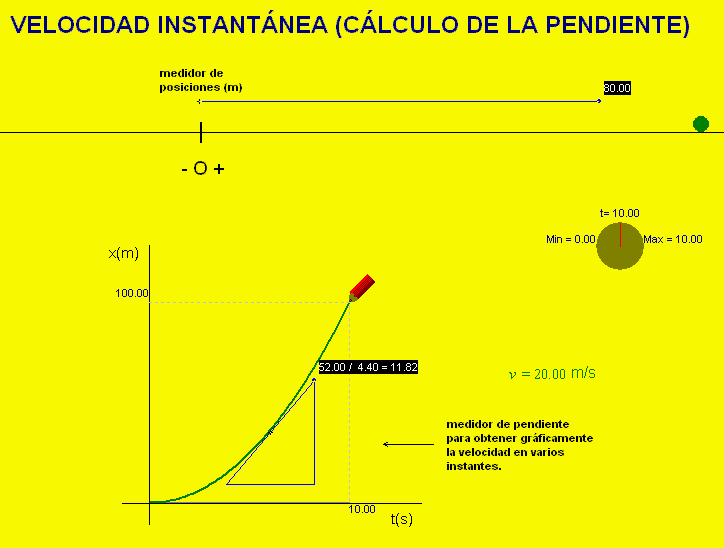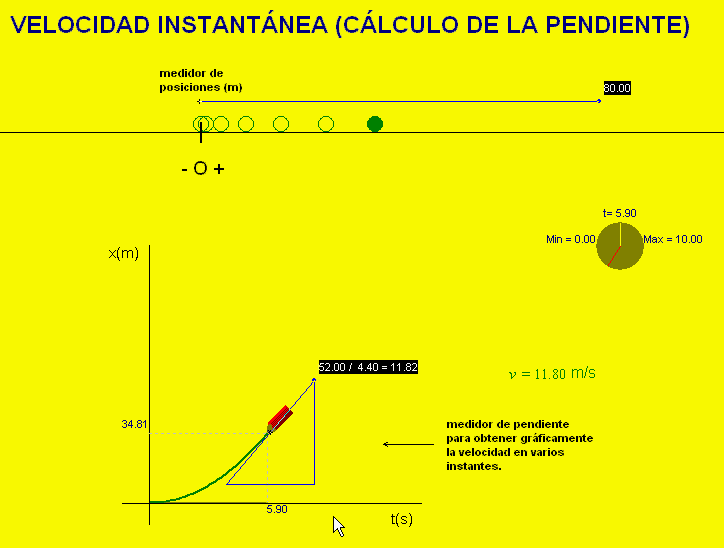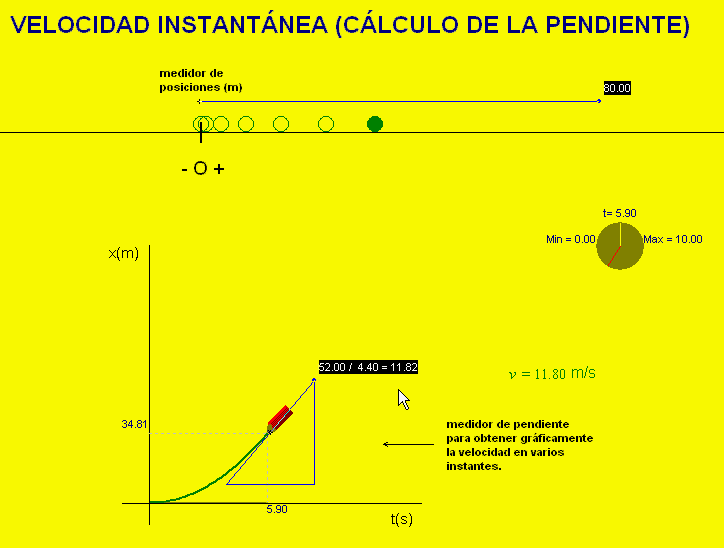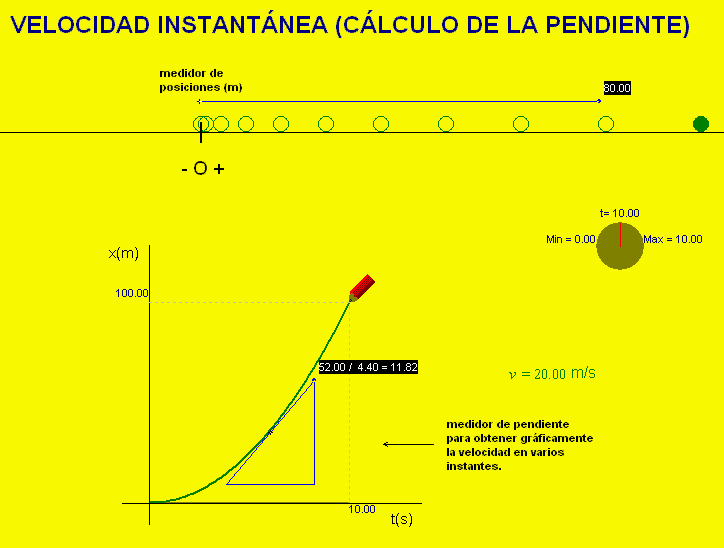
Para practicar este
concepto se puede usar la animación adjunta. Dibuja la
gráfica tiempo-posición de un movimiento e incluye un
medidor de pendientes para obtener la derivada en
cualquier instante. La animación permite comprobar que el valor de la
derivada es el de la rapidez instantánea que se muestra
en la pantalla. Entrando en la ventana de condiciones
iniciales se pueden modificar las características del
movimiento y practicar con todo tipo de ejemplos.
Clic
aquí para
descargar la animación [Si no lo tienes instala
Modellus] |
|
| |
|
Otras magnitudes para
indicar lo rápido que es un movimiento son la rapidez
angular instantánea y el vector representativo de la
velocidad instantánea. La dirección del vector velocidad
es tangente a la trayectoria en cada punto (si el
movimiento es rectilíneo, la tangente es la propia
recta) y su sentido es el de orientarse hacia donde
avanza el móvil. |
| |
|
La mayoría de
movimientos no son uniformes, sino que su velocidad
cambia de forma más o menos complicada a lo largo del
trayecto. La aceleración es la magnitud que
informa de una mayor o menor brusquedad en esos posibles
cambios de velocidad. La relación que tiene la
aceleración respecto de la velocidad es similar a la que
tiene la velocidad tiene respecto de la posición. Es
decir, la aceleración instantánea es la derivada de la
velocidad instantánea. Lógicamente, el vector
aceleración se orienta hacia donde lo hacen los
incrementos de los vectores velocidad. Por tanto, en un
movimiento rectilíneo, el sentido del vector aceleración
coincide con los de los vectores velocidad cuando los
cambios de posición son cada vez mayores y es de sentido
contrario si son cada vez menores. Cuando la trayectoria
es curvilínea, el vector aceleración se dirige siempre
hacia la parte interior de la curvatura, inclinándose a
favor o en contra del movimiento según la describa el
móvil aumentando o minorando sus recorridos. |
|
| |
Índice |
 |
|
|
|
|