|
 |
CAMPO
MAGNÉTICO CREADO POR ALGUNOS TIPOS DE CORRIENTES. LEY DE AMPERE |
 |
|
|
|
| |
|
Una vez establecido que las
corrientes eléctricas producen campos magnéticos, interesó
establecer expresiones operativas que permitan calcular el campo
creado por algunos tipos de corriente. Lógicamente, después de
la experiencia de Oersted, el primer caso que se estudió fue la
corriente rectilínea. |
| |
|
1.
Campo magnético creado por una corriente rectilínea
indefinida |
|
|
|
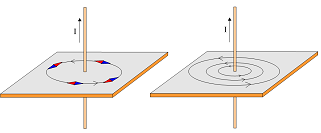
El resultado de la
experiencia de Oersted indica que el campo magnético
producido por una corriente rectilínea es perpendicular
a dicha corriente. Además, el magnetismo natural muestra
que las líneas de fuerza son cerradas en todas las
experiencias. |
|
|
|
|
 |
|
 |
|
Por lo tanto, teniendo en cuenta la
geometría de la situación, es lógico plantear que las
líneas del campo deben ser circunferencias contenidas en
planos perpendiculares a la corriente y con el centro en
el conductor. La veracidad de esta hipótesis se puede comprobar
sencillamente colocando una brújula en diversas
posiciones alrededor de la corriente o espolvoreando en
un plano perpendicular a la corriente limaduras de
hierro, que se imantan y dibujan la líneas del campo
magnético.
A la izquierda: Visualización de las
líneas del campo magnético producido por una corriente
rectilínea |
|
|
|
|
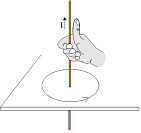
Se constata también que el sentido de las líneas del campo magnético
verifica respecto del de la corriente la llamada regla
de la mano derecha o de cualquier rosca (como la de un
tornillo o un sacacorchos), que ilustra el dibujo
adjunto. Esta regla tiene en cuenta que, como es lógico,
si se invierte el sentido de la corriente eléctrica,
también se invierte el sentido de circulación del campo
magnético.
En cuanto al valor de
la inducción magnética del campo creado por una
corriente rectilínea, viene determinada por: |
|
 |
|
| |
|
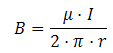 |
| |
|
Esta expresión se conoce como ley de
Biot (1774-1882) y
Savart (1791-1841). Dice que la inducción
magnética es proporcional a
la intensidad de corriente, I, que recorre el conductor,
e inversamente proporcional a la
cantidad 2·π·r,
lo que indica que el campo se va debilitando al alejarnos de
dicho conductor como si se
repartiera en circunferencias de radio r. La inducción magnética además depende
del medio, representado por la constante µ o
permeabilidad magnética. |
| |
|
2.
Campo magnético creado por una espira |
| |
|
 |
|
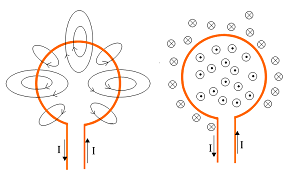
Tiene particular
interés establecer la
forma de las líneas del campo magnético creado por una
espira recorrida por una corriente eléctrica. Para
hacerlo, sirven las
conclusiones obtenidas acerca del campo magnético creado
por un conductor rectilíneo, ya que, aunque la espira
tenga forma curvilínea, podemos razonar tomando pequeños trozos del conductor y asimilándolos
a conductores muy pequeños casi rectilíneos.
Aplicando
este razonamiento se han representado en el dibujo de la
izquierda las líneas
del campo creado por una espira circular de radio R,
mientras que en el dibujo de la derecha se representa dicho campo simbólicamente en el plano de la
espira, mediante puntos y aspas. Un punto indica que ahí
el campo se dirige hacia nosotros y un aspa indica que
ahí el campo lo hace hacia dentro del plano. |
|
| |
|
Resulta muy instructivo considerar
expresamente a la espira como un imán. Así,
la cara de la espira
que mira
hacia nosotros corresponde al polo norte de dicho imán (por ahí
emergen, desde la espira, líneas del campo magnético), mientras
que la cara opuesta (detrás) corresponde al polo sur del imán
(por ahí entran al plano de la espira las líneas del campo
magnético).
En cuanto al valor de la
inducción magnética, es diferente en cada punto que rodea a la
espira y en el punto medio de ella se calcula con la
expresión: |
| |
|
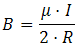 |
| |
|
3.
Campo magnético creado por un solenoide.
|
|
|
|
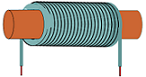
El estudio de la espira,
asimilándola a un imán, sugiere dar un paso más en el diseño del
dispositivo de corriente se asemeje a un imán
natural de geometría rectangular. Dicho paso consiste en
multiplicar el número de espiras arrollando el conductor
una y otra vez. El resultado se denomina solenoide o bobina.
| |
|
 |
|
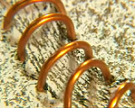 |
|
Las líneas del campo magnético
que produce una sola espira se curvarían
alrededor de ella, pero al colocar sucesivamente
más espiras esas líneas no se pueden curvar para
salir y volver a entrar en la bobina, hasta que
llegamos al extremo del arrollamiento. En
consecuencia, en el interior del solenoide las
contribuciones al campo magnético de cada una de
las espiras se refuerzan y proporcionan un campo
magnético de líneas prácticamente paralelas
entre sí (y paralelas también a la línea que
marcan las espiras)
A la izquierda:
Campo magnético uniforme dentro de un solenoide |
|
| |
|
|
 |
|
 |
|
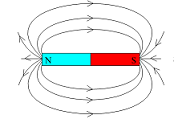
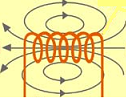
Tal como enseñan los
dibujos adjuntos, la consecuencia de ello es que el
solenoide o electroimán genera un campo magnético, con
geometría muy similar a la
de un imán natural rectangular. Por otra parte, como
el campo magnético depende del medio, con objeto de
aumentar aún más su intensidad se puede incluir en el
interior del solenoide un pedazo de hierro dulce.
A la izquierda: Comparación
entre el campo magnético creado por un imán y el
creado por un solenoide |
|
|
|
|
La permeabilidad
magnética de este material es muy elevada y así se
consigue un electroimán, de inducción controlable
(modificando la intensidad de la corriente) e intensa,
cuyas líneas de fuerza son semejantes a las creadas por
un imán natural y rectangular. |
|
 |
|
|
|
|
Para bastantes aplicaciones es
más interesante utilizar el campo magnético creado en el
interior del solenoide. Si la bobina es rectilínea, en puntos suficientemente alejados de los extremos
dicho campo es prácticamente uniforme, y su valor
es proporcional a la intensidad
de la corriente que circula por las espiras, I, a la
permeabilidad magnética del medio,
µ,
y a la densidad lineal de espiras (es decir, al número de
espiras, N, por unidad de longitud, L): |
|
|
|
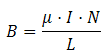 |
|
|
|
Los ejemplos expuestos,
muestran que, con diseños de
corrientes eléctricas adecuados, se pueden producir campos
magnéticos de geometría e intensidad controlables. En relación
con estos conceptos,
Ampere (1775-1836) obtuvo en
1826 una relación general entre la intensidad de corriente
eléctrica que pasa por un hilo y el campo magnético que produce.
Posteriormente la corrigió
Maxwell (1831-1879) y la
incluyó en un conjunto de cuatro ecuaciones (ecuaciones de
Maxwell) que fundamentan la teoría electromagnética clásica. En
el documento vinculado se puede consultar la
ley de Ampere y su
aplicación para deducir las expresiones que calculan el campo magnético
de algunos tipos de corriente. |
|
| |
Índice |
 |
|
|
|