| |
|
 |
SELECTOR
DE VELOCIDADES DE PARTÍCULAS CARGADAS |
 |
|
|
|
| |
|
En presencia de un campo eléctrico (E) y un
campo magnético (B) la fuerza total
electromagnética que se
ejerce sobre una carga (q) es: F = q (E
+ v x B). Por ello, combinando
adecuadamente los dos campos (E y B),
se puede seleccionar a las partículas cargadas
que tengan un valor determinado de la velocidad
(v).
|
|
|
|
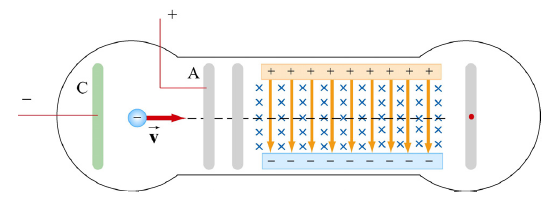
A la derecha se expone un dibujo de un
selector de partículas aplicado a
electrones. Tales electrones son
emitidos por un cátodo (C) y aceleran
hacia el ánodo (A). A continuación se
les aplica un campo eléctrico E y
un campo magnético B (ambos
uniformes).
Tal como muestra el dibujo,
la orientación de tales campos es
adecuada para ejercer sobre los
electrones fuerzas de sentido opuesto.
En estas condiciones la selección de
electrones en función de su velocidad se
basa en que la intensidad de los campos
sea la precisa para que la fuerza total
sobre ellos sea cero. Los electrones que
cumplen esta condición no se desvían de
su trayectoria y, por tanto, inciden
exactamente en el lugar indicado por el
punto de color rojo.
|
|
 |
|
|
|
|
|
Como el módulo
de la fuerza eléctrica es Fe = e·E y el de la
fuerza magnética es Fm = e·v·B, al igualar
ambas, se deduce que la velocidad de los electrones
seleccionados es:
v = E/B
(1) |
|
|
|
Los electrones
adquieren esa velocidad (v) y/o la energía cinética
correspondiente (Ec = m·v2/2)
en su camino entre el cátodo y el ánodo, a lo largo del cual se
les aporta una energía eléctrica (W = e·ΔV):
e·ΔV = m·v2/2 (2) |
|
|
|
|
De modo que (combinando las
ecuaciones 1 y 2) se cumple la siguiente relación entre la carga
y la masa de los electrones: |
|
|
|
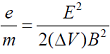 |
|
|
|
|
|
| |
Índice |
 |
|
|
|
|
|