| |
|
 |
EXTENSIÓN DEL MODELO CINÉTICO-CORPUSCULAR A LÍQUIDOS Y SÓLIDOS |
 |
|
|
|
| |
|
Nos planteamos
ahora en qué medida es posible extender el modelo
cinético-corpuscular de los gases a los sólidos y los líquidos.
|
| |
 |
|
De
entrada hay que dejar constancia de límites de
aplicabilidad del modelo a los propios gases. Dicho
modelo considera que las
eventuales interacciones entre las partículas del gas
son asimilables a simples choques elásticos, lo cual
puede ser aceptable únicamente en la medida en que
dichas partículas mantengan su movimiento y sean
diminutas en comparación con las distancia media que las
separa. Estas condiciones dejan de cumplirse cuando el
gas se
comprime de forma apreciable y cuando se enfría en
exceso. Por ello a la ley de los gases, sustentada en el
modelo, se le llama de gases ideales, entendiendo
que los gases reales sólo la cumplen con un cierto grado
de aproximación y que su fiabilidad decae cuando, por
ejemplo, la presión, P, aumenta o la temperatura,
T, disminuye. |
|
| |
|
Estos hechos
muestran que el modelo
cinético-corpuscular tiene que ser matizado o modificado para
poderse aplicar a sólidos y a líquidos. Al mismo tiempo, en el otro
platillo de la balanza hay que considerar que bastantes
propiedades de los gases que sustentan al modelo, también las
tienen, aunque menor grado, sólidos y líquidos. Así por ejemplo,
los líquidos y los sólidos también se dilatan cuando se
calientan, bastantes líquidos se pueden mezclar con facilidad,
etc. La compresibilidad también puede ser vista, con este
planteamiento, como una propiedad que no es drásticamente
distinta entre los gases y el resto de la materia. Los sólidos y
los líquidos son muy poco compresibles, pero tampoco lo son
excesivamente los gases, como se comprueba
cuando, después de haber apretado bastante el émbolo de una
jeringa grande, llega un momento en que ya no resulta nada fácil
seguir comprimiendo el aire encerrado. |
|
|
 |
|
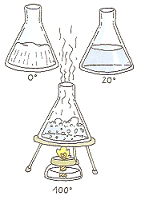
Para extender el modelo
cinético-corpuscular a líquidos y sólidos, nos fijamos
en el hecho de que todas las sustancias se pueden
encontrar en los tres estados, dependiendo de la presión
y la temperatura.
Ello indica que
han de existir fuerzas atractivas entre las partículas,
unas fuerzas que apenas tienen influencia a grandes
distancias o entre partículas con altas velocidades (es
decir, en los gases), pero que, en cambio, deben ser
intensas a distancias cortas o entre partículas con
velocidad menor (en los líquidos y sólidos)
Así se explica satisfactoriamente, por
ejemplo, la diferencia
de volumen cuando un gas pasa al estado líquido y al
sólido. En estos dos estados las
partículas están ligadas por las fuerzas
de atracción entre ellas, aunque permitiendo
movimientos de vibración (o de otro tipo), más o menos amplios
según la temperatura. |
|
| |
|
Otro aspecto en
que nos fijamos es el hecho de que al pasar de líquido a sólido la
materia pierde la propiedad de "fluir", es decir, de difundirse.
Esto hace pensar que el modo y la intensidad con que las las
fuerzas atractivas retienen a las partículas es diferente en
ambos estados. |
| |
|
En el
caso del líquido las partículas dejan "huecos" en la
estructura, de tal forma que, además de vibrar, grupos
de partículas se pueden desplazar ocupando
alternativamente esos huecos. Así se explica que los
líquidos se adapten a la forma del recipiente y también
que bastantes se mezclan con facilidad.
En cambio, las
partículas de los sólidos no pueden realizar este tipo
de desplazamiento, siendo posible únicamente movimientos
de vibración de cada partícula entre las que la rodean.
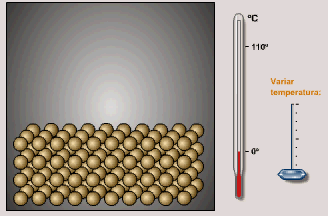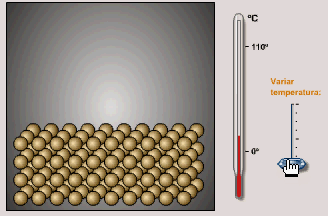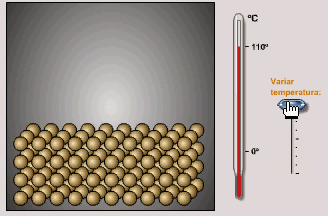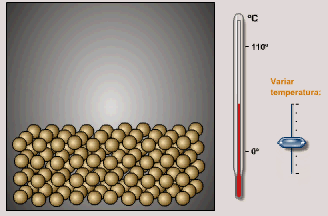
Esta imagen de la estructura cinético-corpuscular de los
sólidos es coherente con el hecho de que tienen una
forma definida, que corresponde a la estructura ordenada
de sus partículas: Tal como simula la animación adjunta,
al aumentar la temperatura aumenta la
velocidad de los movimientos de vibración de las
partículas, pero no cambia esa estructura mientras no se
produzca un cambio de estado. |
|
 |
|
|
|
|
Mediante el modelo
también se establecen las condiciones requeridas para que
se produzcan cambios de estado. Por ejemplo, para que un
gas se convierta en líquido es necesario disminuir la
velocidad de las partículas (enfriar el gas) y/o reducir las
distancias entre ellas (comprimir el gas), con tal de conseguir
que
las fuerzas atractivas lleguen a ser de la intensidad
suficiente. Análogamente sucede para el paso de líquidos a
sólidos. |
|
|
|
Todas estas
consideraciones destacan
la funcionalidad del modelo cinético-corpuscular de la materia.
No obstante, conviene saber que, cuando se profundiza, se constata
la complejidad que puede tener el modelo en muchas situaciones, debido a la propia
complejidad que presenta la estructura interna de la materia. A
modo de ejemplo de ello, podemos mencionar cómo algunos aspectos que presenta el comportamiento del agua
en los tres estados son todavía objeto de estudio. En 2011
se publicaron los resultados de una investigación sobre el
proceso de congelación del agua, a la que se aplica el modelo
cinético-corpuscular mediante un proceso de modelización
avanzada. |
|
|
 |
|
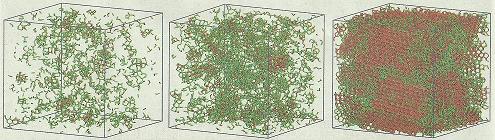
En dicha
investigación se explica el hecho curioso de que, en
circunstancias específicas, el agua no se congela por
debajo de cero grados, sino que se puede mantener
líquida hasta -48 ºC. Para interpretar este hecho, el
ordenador simuló el comportamiento de un número
"grande" de moléculas (exactamente fueron 32 768, una
cantidad significativa, pero todavía inferior a las que
componen una gota de agua), con objeto de determinar los
cambios (en la capacidad térmica, la densidad y la
compresión) del agua al "superenfriarse" y simular la
velocidad de cristalización del hielo.
A la izquierda: Modelización por
ordenador del proceso de congelación del agua |
|
|
|
|
El agua se
puede mantener líquida hasta los 48 grados bajo cero
(30-11-2011) |
|
| |
Índice |
 |
|
|
|
|
|
