| |
|
 |
MOVIMIENTO DE CUERPOS EN EL CAMPO GRAVITATORIO TERRESTRE.
POSIBLES TRAYECTORIAS |
 |
|
|
|
| |
|
 |
|
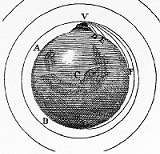
En el
tema sobre
Tiro horizontal y su contribución a las Síntesis
Newtoniana se expone y se comenta con
detalle el "histórico" dibujo
adjunto. Muestra diferentes trayectorias que,
dependiendo del valor de su velocidad inicial, puede seguir un
objeto lanzado horizontalmente desde una colina
(señalizada en el dibujo mediante la letra V).
Estas trayectorias dependen de cuál sea el valor
de esa velocidad inicial horizontal con la que
sea lanzado el objeto. |
|
|
|
|
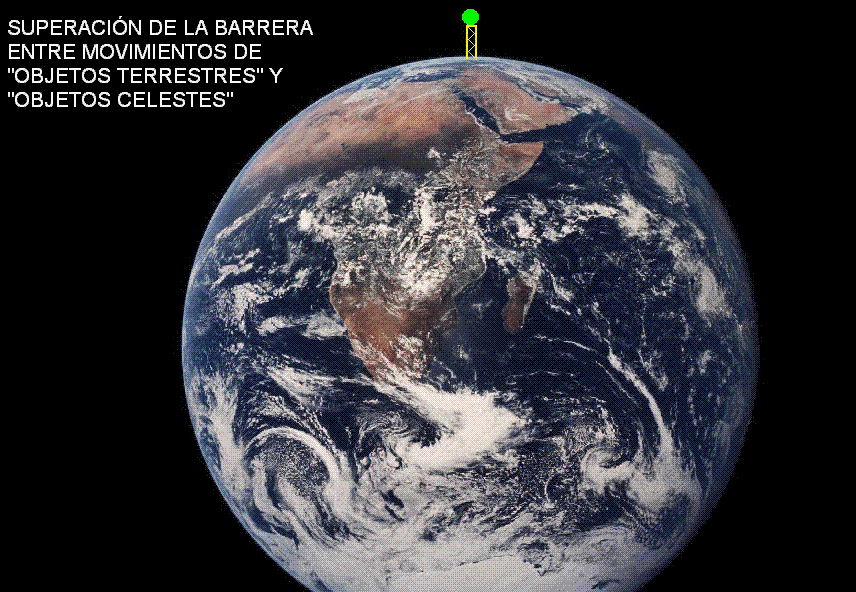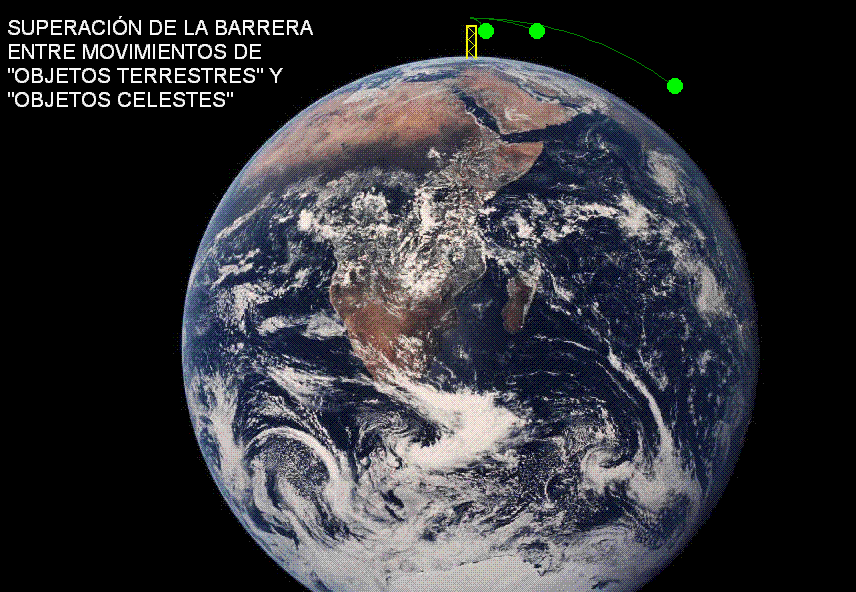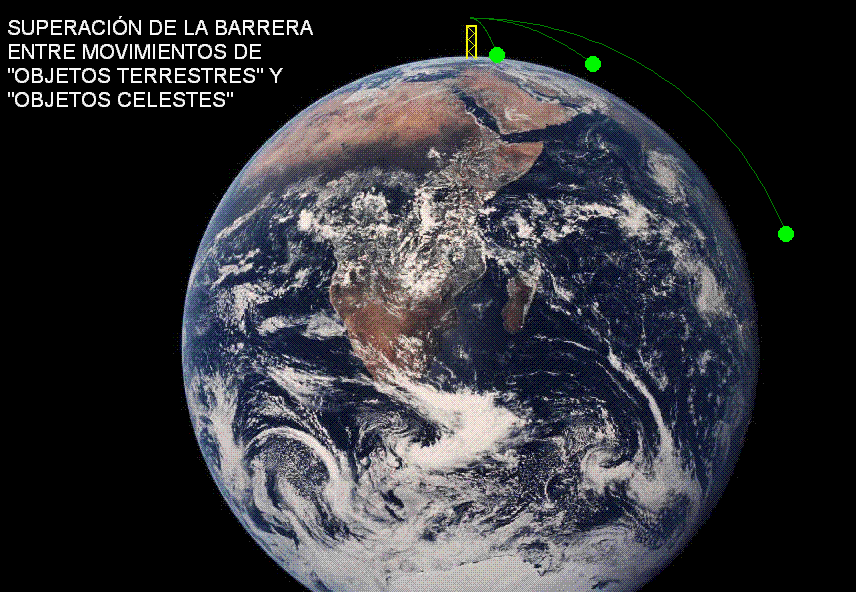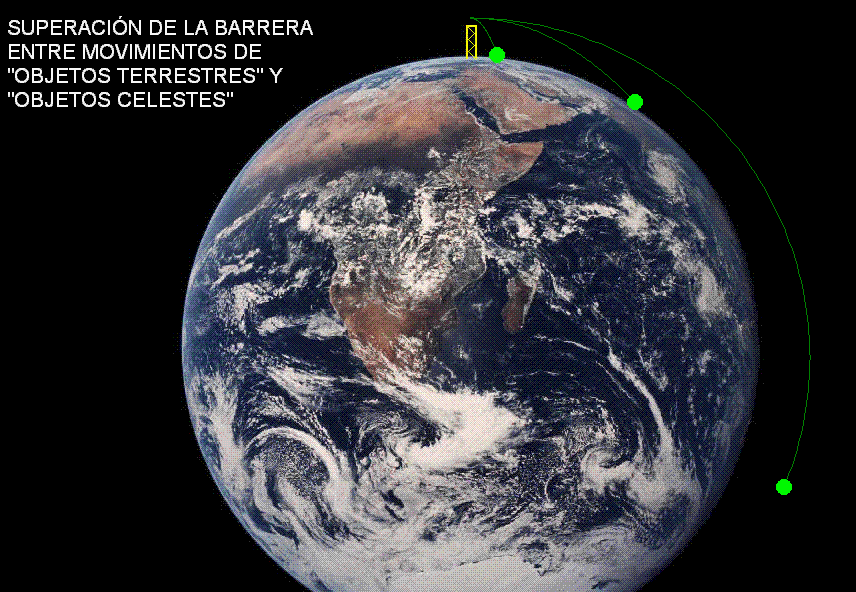
La misma situación
la recrea la animación Modellus
adjunta (debajo), que simula el movimiento
de tres cuerpos lanzados horizontalmente.
Uno de ellos
se lanza con
la velocidad inicial adecuada para colocarse en
órbita.
Los otros dos se lanzan con velocidades
iniciales inferiores y realizan
movimientos elípticos antes de chocar
con el suelo (para una velocidad muy pequeña, y
una altura también muy pequeña, ge podría
considerarse casi constante y la elipse se
acercaría mucho a una parábola).
Clic
aquí para descargar esta animación.
Para usarla en tu ordenador, instala
Modellus |
|
 |
|
|
|
|
Al considerar estos conceptos se pone en
evidencia que no existen diferencias
fundamentales entre, por ejemplo, el movimiento
orbital de un satélite y el movimiento
casi parabólico de una pelota que haya sido lanzada
con muy poca velocidad desde la colina y termine chocando contra el
suelo. Para estudiar ambos movimientos se
requiere usar unas mismas leyes fundamentales, y dichos movimientos representan dos
soluciones particulares de un único problema
general: El estudio de movimientos de objetos
bajo la influencia del campo gravitatorio
producido por un cuerpo celeste, en este caso,
la Tierra. |
|
|
|
Las
leyes generales a aplicar en estos problemas son la
ley
de gravitación universal y los
principios de la
dinámica de Newton. Conjuntamente permiten escribir una ecuación
general para el movimiento de cualquier cuerpo sometido
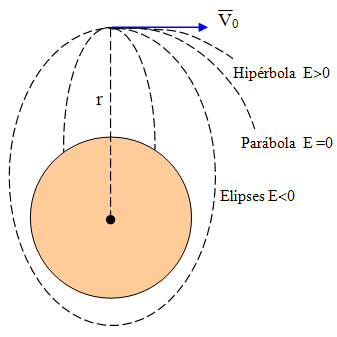
a la atracción gravitatoria de la Tierra. Dependiendo de los valores que adopten los
parámetros intervinientes (velocidad inicial, distancia entre
la Tierra y el cuerpo), se obtienen diferentes
soluciones o, lo que es igual, varias trayectorias posibles
del cuerpo: movimiento rectilíneo vertical,
movimiento parabólico, órbita circular, órbita elíptica
o trayectoria hiperbólica. |
|
|
|
Estas soluciones también se
pueden prever con un planteamiento energético. El sistema formado por la Tierra y el
cuerpo tiene energía cinética positiva (Ec =
mv2/2) y energía potencial gravitatoria
negativa (Epg = - GMm/r). En el balance
de la energía total, caben tres posibilidades:
a) Que
la energía total sea negativa, es decir, que la energía
potencial en valor absoluto sea mayor que la energía
cinética. En ese caso, el objeto está ligado al planeta
(cae al suelo terrestre o permanece en órbita elíptica o
circular)
b) Que la energía total sea nula, es decir que el valor
absoluto de la energía potencial coincida en todo
momento con el valor de la energía cinética. En ese
caso, el objeto se puede alejar indefinidamente de la
Tierra y a una distancia infinita su velocidad
sería 0. La velocidad que tiene el objeto en este caso
especial se llama
velocidad de escape (deducción de su expresión en
este documento) y describe una parábola.
c) Que la
energía mecánica sea positiva, es decir, que la energía
cinética siempre supere al valor absoluto de la energía
potencial. Al satélite le sobre energía cinética para escapar de
la atracción gravitatoria terrestre y describe una hipérbola. |
|
 |
|
|
|
|
En
este documento se expresa de forma operativa
el problema general del movimiento de un objeto sometido
al campo gravitatorio de, por ejemplo, un
planeta o de una estrella. |
|
|
|
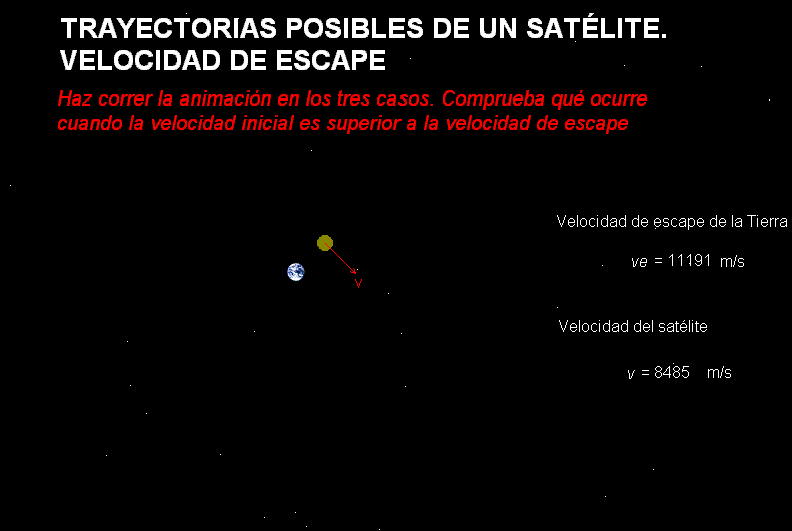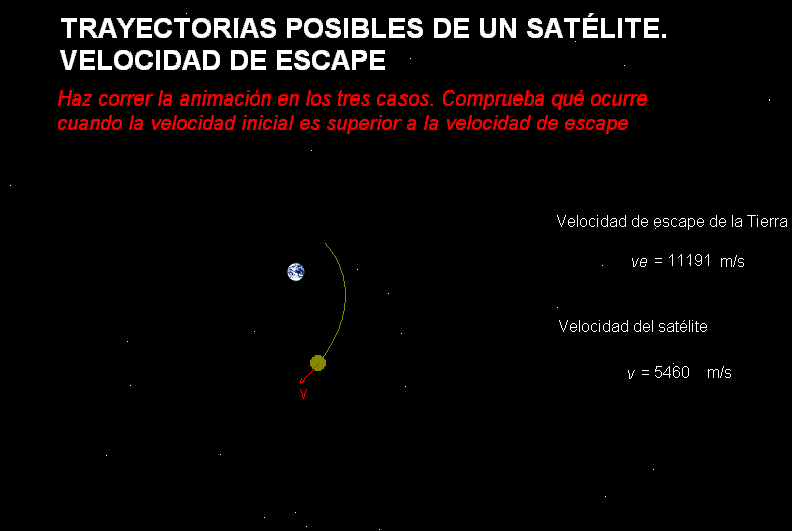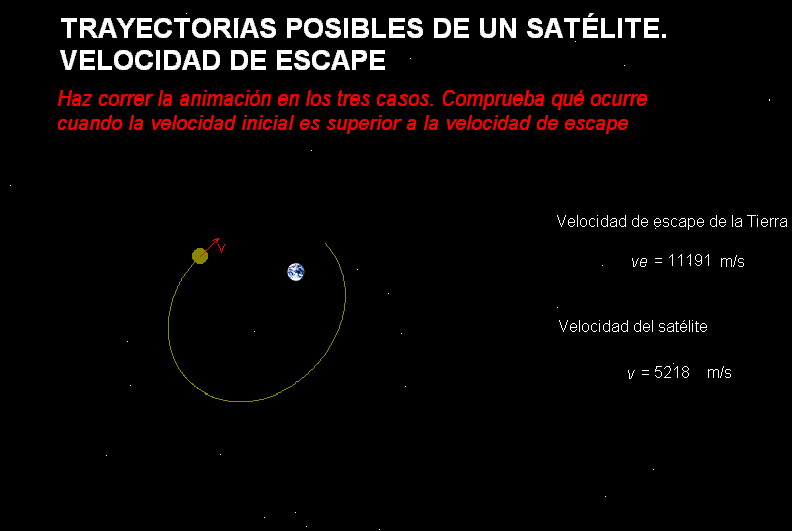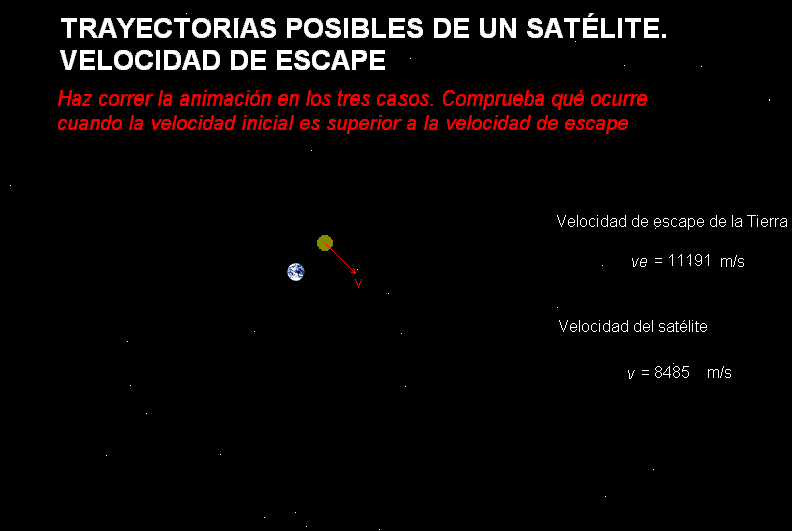
Por su
parte,
la
animación adjunta, representa diferentes
trayectorias que puede tener cualquier cuerpo
que se halla lanzado desde la Tierra, dependiendo de su velocidad de
lanzamiento (ignorando el rozamiento que tendría
lugar si atravesara la atmósfera).
Inicialmente se muestran tres casos (órbita elíptica, órbita límite a
la velocidad de escape y órbita hiperbólica abierta),
pero el usuario puede manipular la animación, ampliando el estudio a cualquier
otro valor de la velocidad inicial del cuerpo.
Clic
aquí para descargar esta animación.
Para usarla en tu ordenador, instala
Modellus |
|
 |
|
|
|
| |
|
|
| |
| |
Índice |
 |
|
|
|
| |
|
|
|