| |
|
 |
MODELOS SOBRE EL CAMPO GRAVITATORIO EN EL INTERIOR DE LA TIERRA |
 |
|
|
|
|
|
|
Teniendo en
cuenta la estratificación del subsuelo terrestre, cabe
plantear varios modelos para calcular la evolución del
campo gravitatorio de la Tierra con la profundidad. Uno
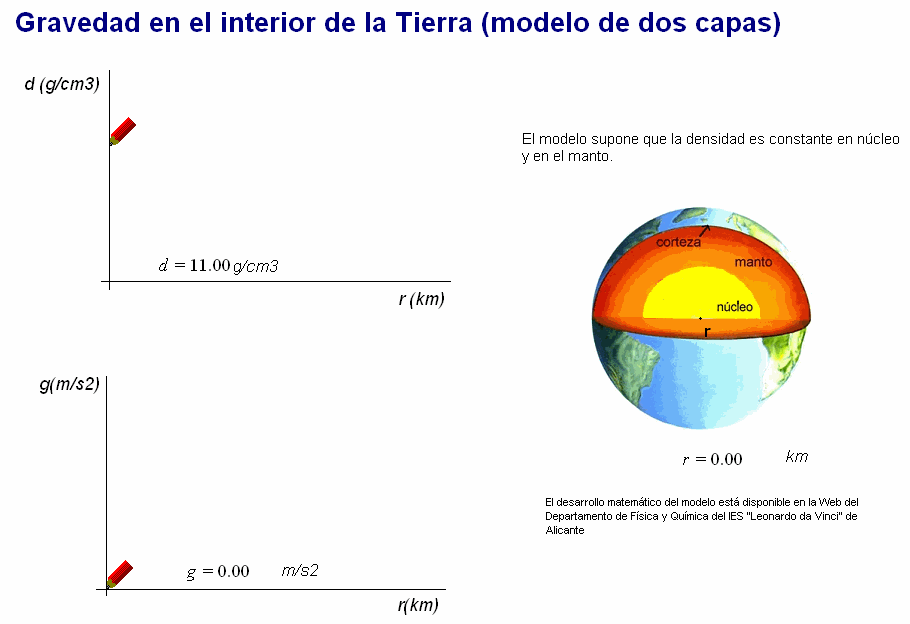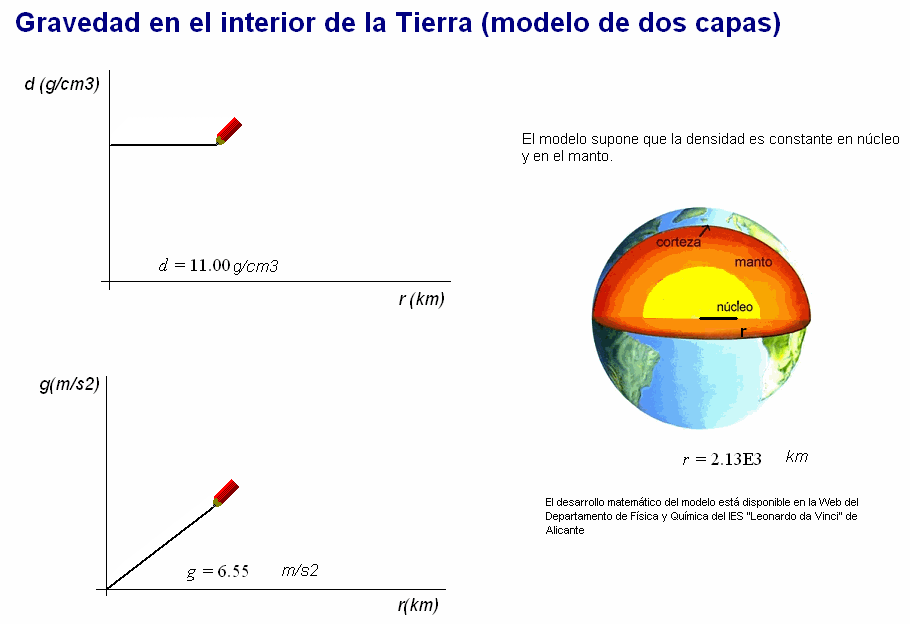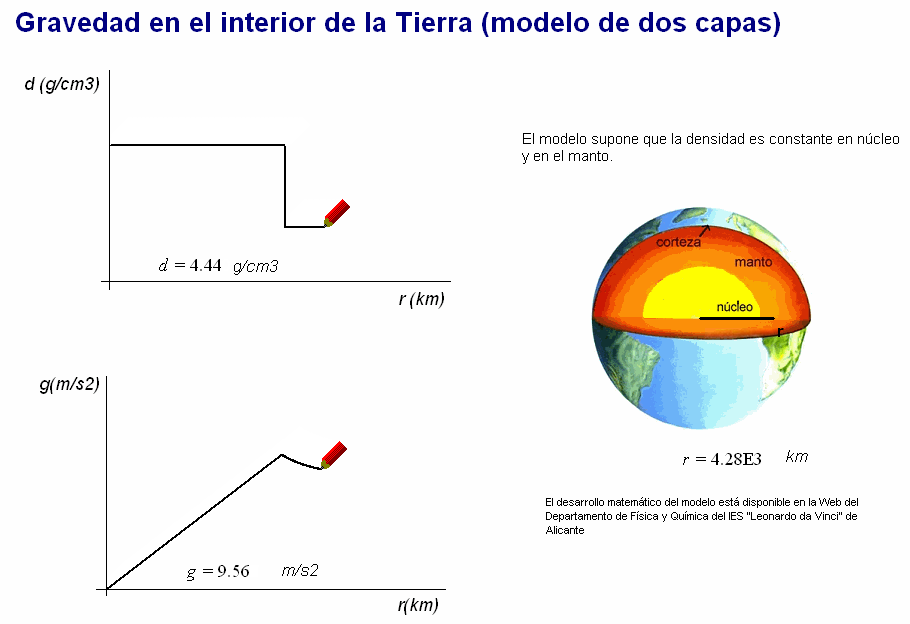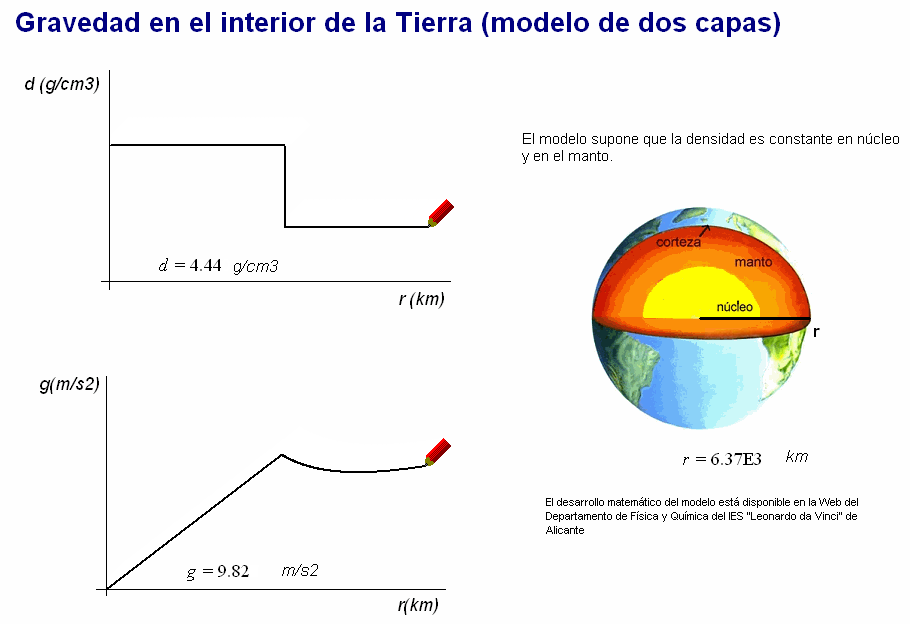
muy sencillo consiste en dividir a la Tierra en sus dos capas principales: el núcleo
(esfera interior de radio 3 490 km) y el manto
(capa esférica que va desde núcleo hasta la superficie).
Existe un salto muy brusco en el valor de la densidad
media del núcleo (11,0 g/cm3) y la del
manto (4,44 g/cm3), de tal modo que se
puede suponer que cada una de ellas tenga una densidad
constante.
|
|
|
|
Entonces, al
desarrollar matemáticamente el modelo
(desarrollo en
este
documento) se obtiene el curioso resultado de
que g alcanza un valor máximo (mayor que el
valor de la superficie: 9,8
m/s2) a la altura donde termina
el núcleo y empieza el manto terrestre.
En
el manto g varía poco en términos relativos,
disminuyendo al principio y aumentando al final:
su valor mínimo en esa zona es 9,32 m/s2 (a
1 370m
de profundidad) y desde ahí g vuelve a
aumentar hasta llegar a la superficie, donde
vale 9,8 m/s2.
Este resultado se
muestra en la animación adjunta.
Clic
aquí
para descargar esta animación. Para usarla en tu
ordenador,
instala
Modellus 3 |
|
 |
|
|
|
|
Desde luego,
la densidad de la Tierra no es constante en sus capas
principales. Por ello, en lugar de considerar dos (o
más) capas de densidad constante, un modelo alternativo
plausible consiste en suponer una disminución progresiva
de la densidad de la Tierra al ir desde el centro hasta
la superficie.
|
|
|
|
 |
|
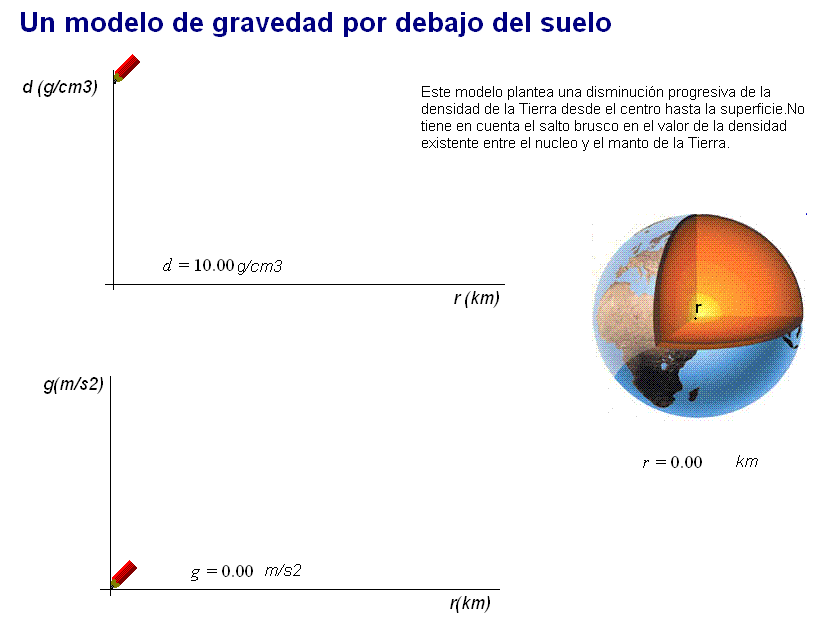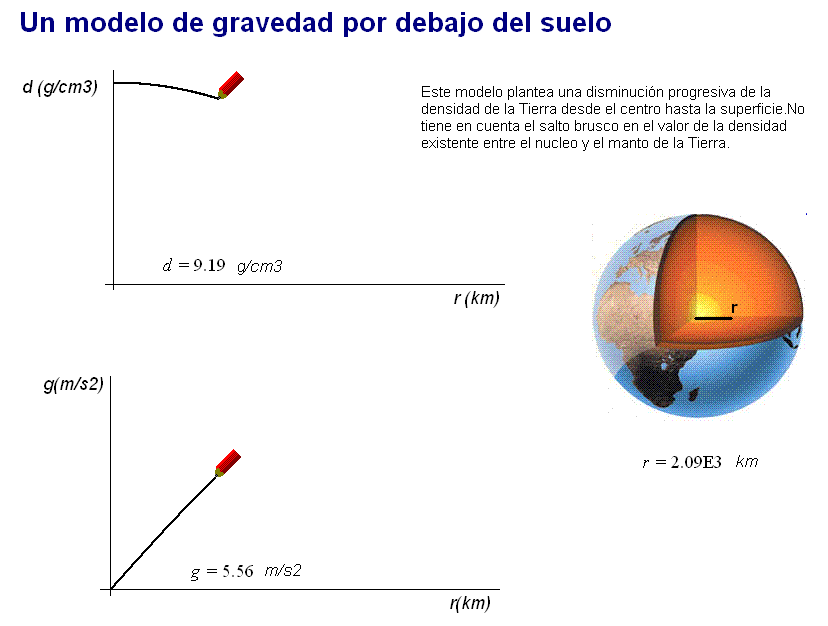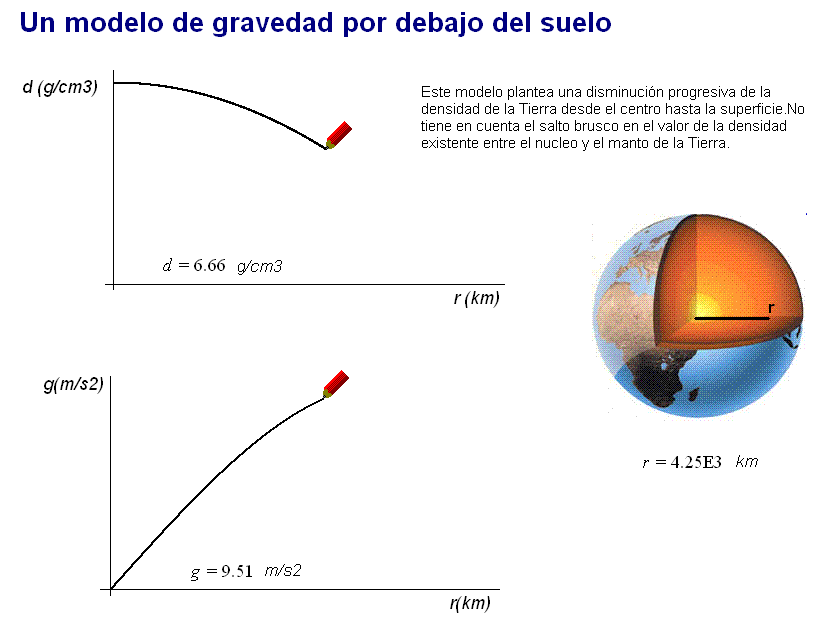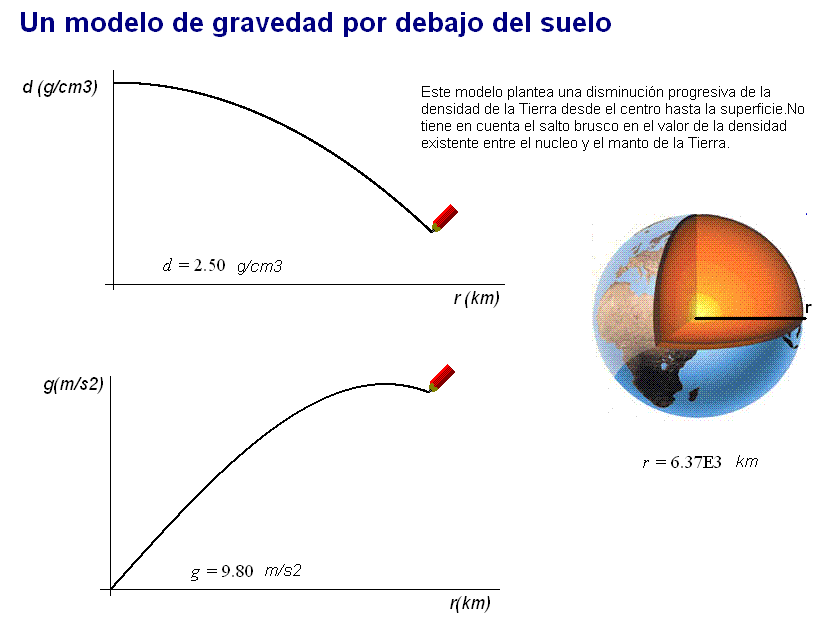
Con una
expresión adecuada coherente con este
planteamiento (desarrollo en
este documento), también se obtiene un valor
máximo de g (igualmente superior a 9,8 m/s2) en
un punto situado por debajo del suelo terrestre.
Igual
que ocurre al aplicar
el modelo anterior, al aplicar éste, a partir de ahí g decrece
lentamente hasta la superficie, donde vale
9,8 m/s2.
Este resultado se
muestra en esta segunda animación.
Clic
aquí
para descargar esta animación. Para abrirla y
manipularla en tu ordenador,
instala
Modellus |
|
|
| |
Índice |
 |
|
|
|
|
|
|