| |
|
 |
EXPERIMENTOS
CON MODELLUS Y SIMULACIONES SOBRE LA CAÍDA EN EL
AIRE Y EN EL AGUA |
 |
|
|
|
|
| |
|
|
| |
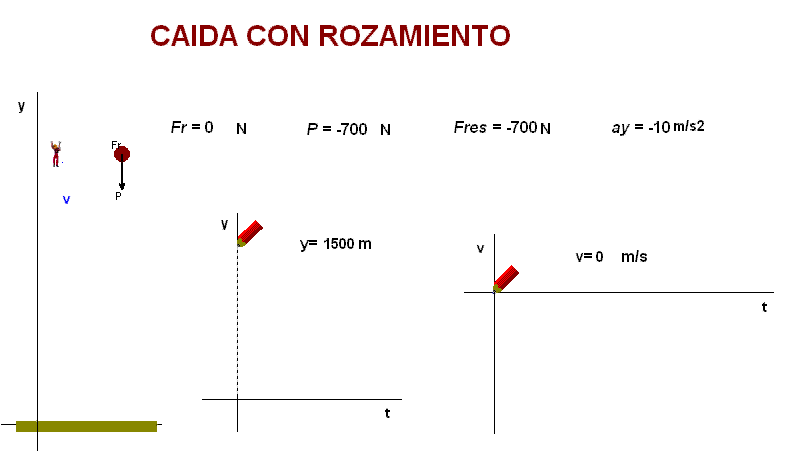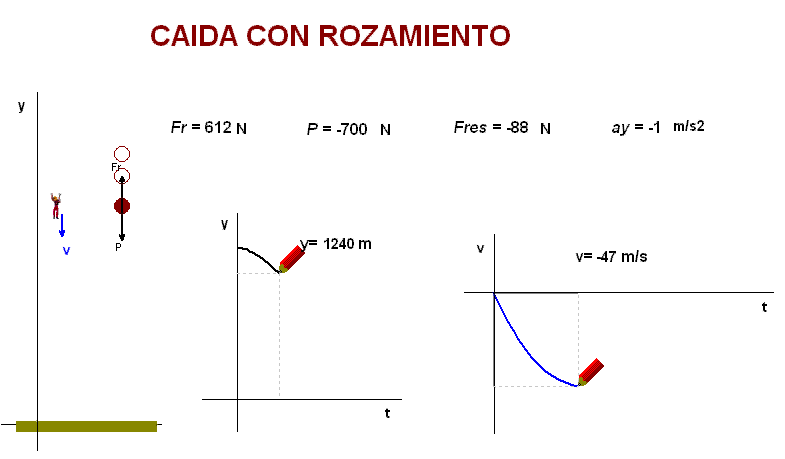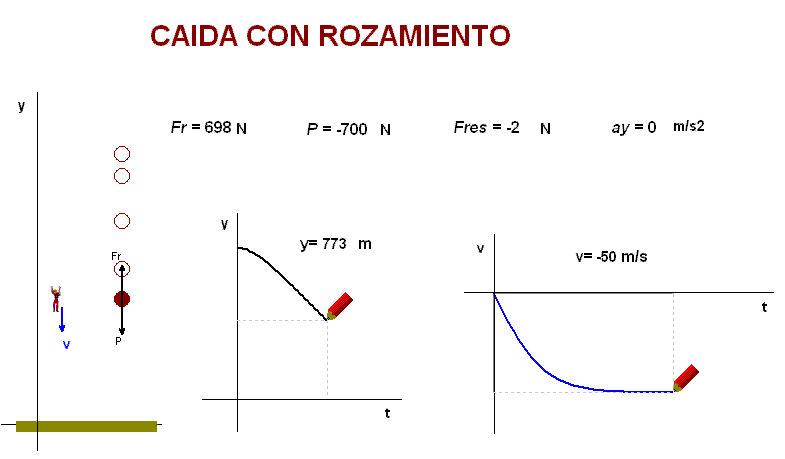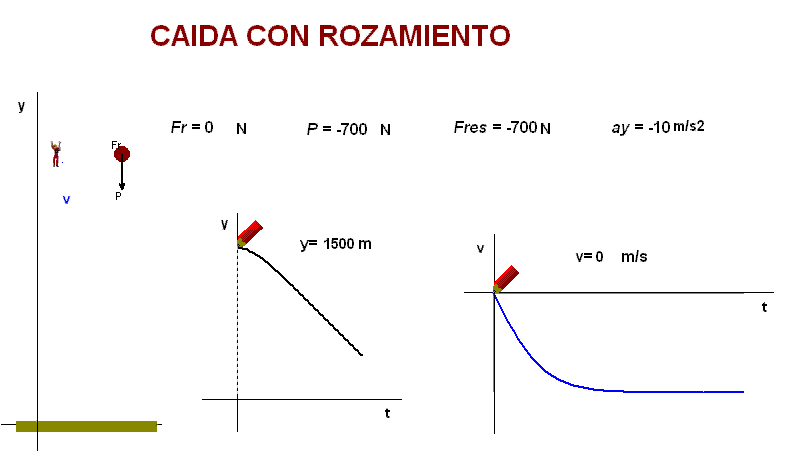
Además de estudiar
experimentalmente la caída en la atmósfera con
rozamiento, usamos el programa
Modellus para simularla (debajo). En el modelo
físico-matemático de la simulación se incorpora una fuerza
de resistencia ejercida por la atmósfera, proporcional a la velocidad para velocidades
pequeñas (régimen laminar) y proporcional al
cuadrado de la velocidad para velocidades más elevadas.
El coeficiente depende del volumen del objeto, su forma
más o menos aerodinámica (que le puede facilitar o
dificultar su penetración a través del aire), el
material, etc. La animación
adjunta enseña que, teniendo en cuenta estos factores, se predice un movimiento de
caída inicialmente acelerado (con una aceleración
decreciente) y, una vez alcanzada la
velocidad límite, uniforme. |
|
| |
|
|
| |
|
|
| |
|
|
| |
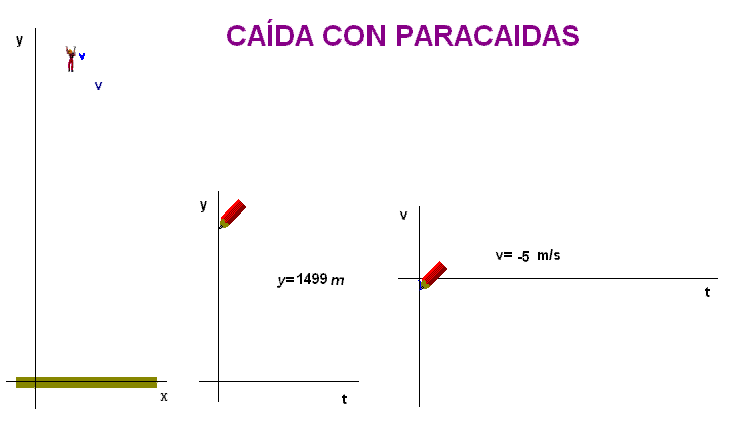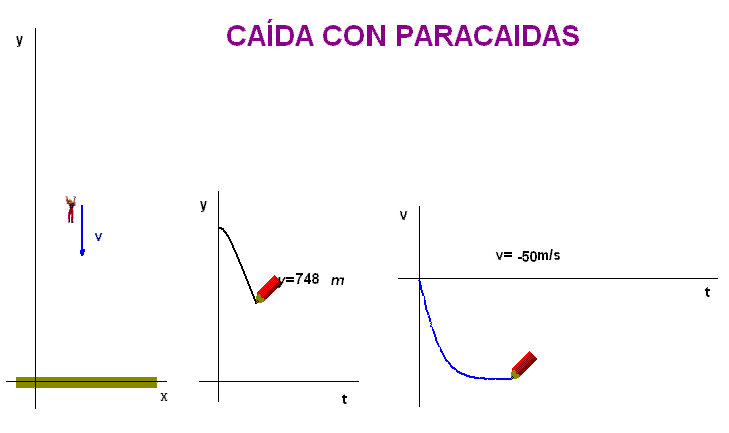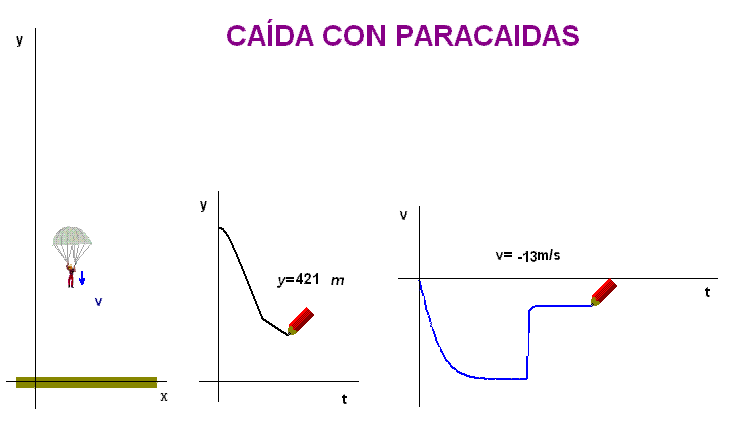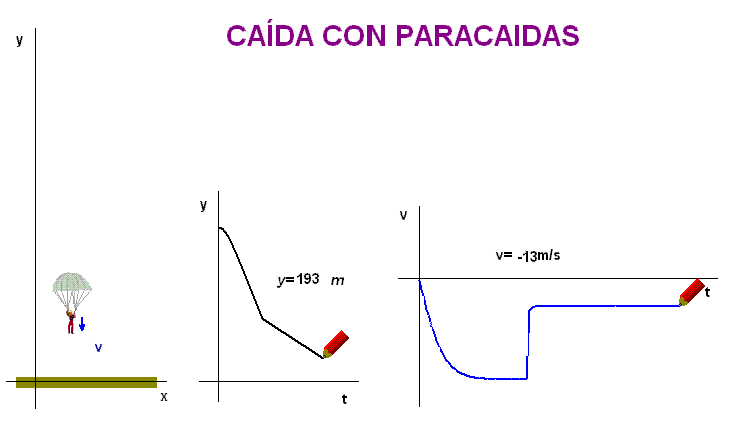
La velocidad límite
de caída de una persona en el aire es bastante elevada
(se puede estimar un valor algo superior a 50m/s),
desde luego excesiva para que llegue al suelo un ser
humano con esa
velocidad. Por eso son
imprescindibles los paracaídas. En la animación adjunta
(debajo) hemos incorporado un paracaídas. En el
momento de su apertura disminuye bruscamente la
velocidad, lo que es equivalente a plantear en el modelo
físico-matemático una modificación repentina de la
velocidad límite. |
|
| |
|
|
| |
|
|
| |
|
|
| |
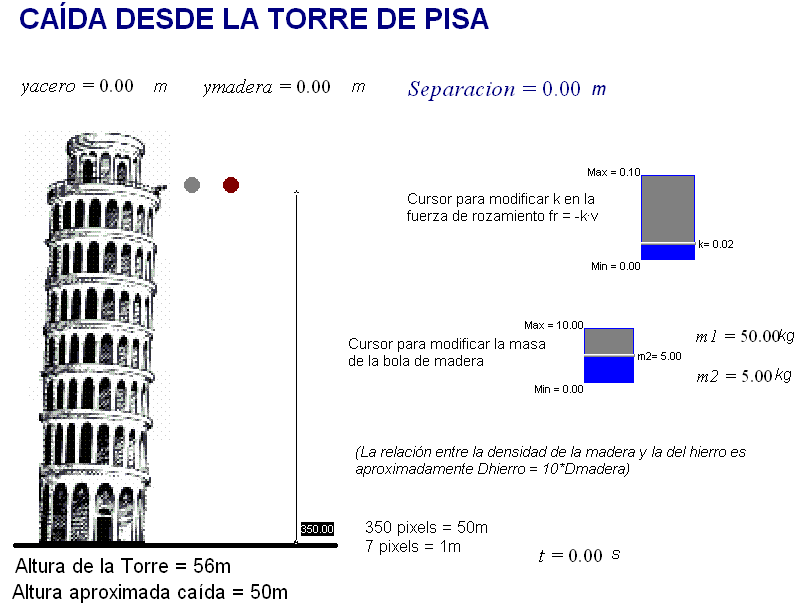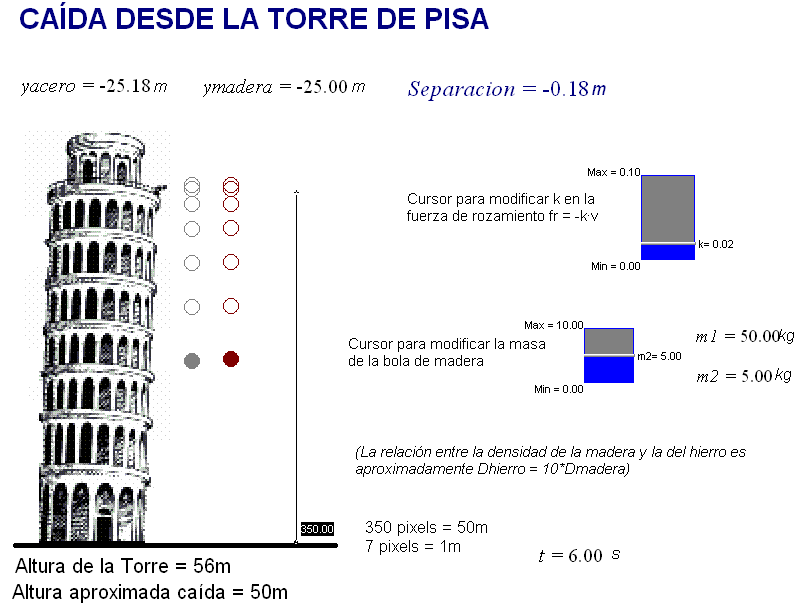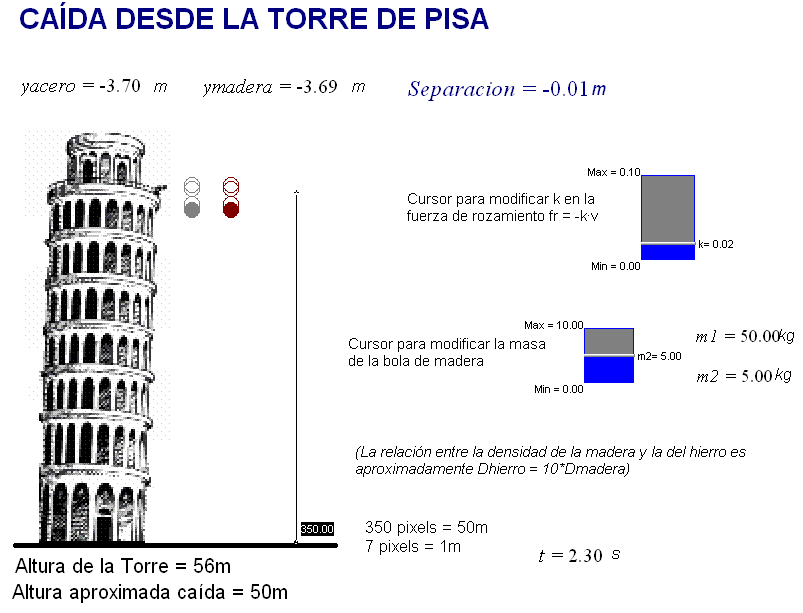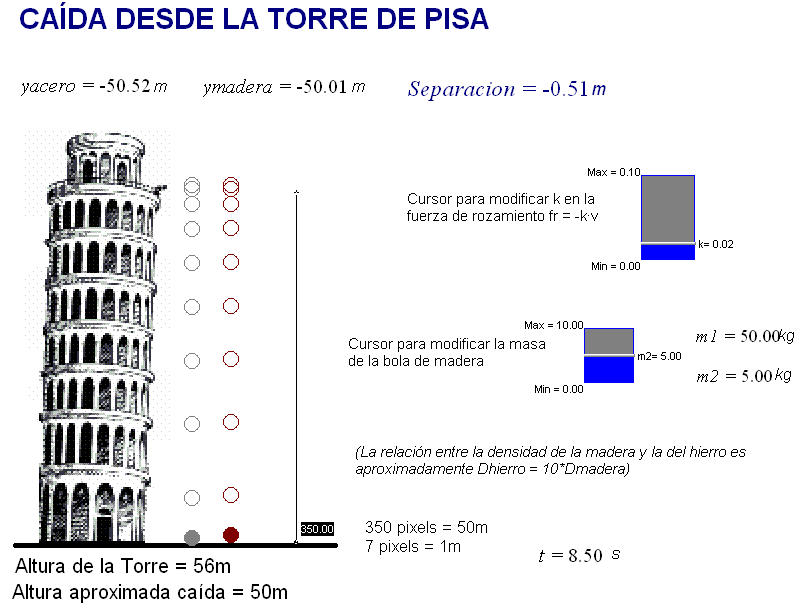
Por otra parte, el
concepto de velocidad límite permite comprobar que
Galileo muy probablemente no realizó el famoso experimento de la
Torre de Pisa y, si lo hizo, no obtuvo el resultado que
dice la leyenda, tal como se suele contar, según la cual el propio Galileo
habría dejado caer desde lo alto de la Torre dos bolas
de masas muy diferentes (quizá de hierro y de madera) y algunos de sus
discípulos habrían comprobado a pie de Torre la caída
simultánea de ambas bolas. |
|
| |
|
|
| |
|
 |
|
Conviene saber que, aunque como hemos dicho la leyenda se suele contar de
este modo, el propio Galileo, realizara o no el
experimento, admitió en un
pasaje de sus diálogos que "las dos bolas
llegaron con uno o dos cúbitos de diferencia (unos 0’5
m)". Galileo atribuyó esa
diferencia a un mero error experimental y destacó que en
todo caso tal diferencia es muchísimo menor que la que
se obtendría según Aristóteles, quien había afirmado que
si un cuerpo pesa el doble que otro, también cae el
doble de rápido.
Modificando las condiciones iniciales
de los movimientos que simula la animación adjunta (en
el gif adjunto vemos que se han ajustado esos parámetros
para obtener el resultado que dijo Galileo que había
obtenido) se
constata que, al intervenir la fuerza de rozamiento del
aire,
la masa inercial y la masa gravitatoria
no se cancelan y, como consecuencia de ello, dos objetos
de masa diferente adquieren aceleraciones diferentes y
tienen una velocidad límite diferente (tanto más
diferente cuanto menor sean ambas masas)
Clic
aquí
descarga la animación. Si no lo tienes, descarga
Modellus 2.5 (32 bits) o
Modellus 3 (64 bits) |
|
|
| |
|
|
| |
|
Un movimiento
interesante de caída dentro de fluidos es el de un
cuerpo sumergido en agua. En este caso, es lógico
esperar que se alcance enseguida la velocidad límite. La
densidad de agua (mucho mayor que la del aire) hace al
empuje ser muy apreciable. Además, la fuerza de
rozamiento es también mucho mayor que en el aire. En
consecuencia, se prevé que el descenso del objeto
corresponda enseguida a un movimiento uniforme a esa
velocidad. |
|
|
 |
|
 |
|
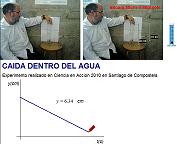
Para comprobar estas hipótesis
se puede realizar un experimento que estudie el movimiento de caída de una esferita dentro
de una probeta llena de agua. La imagen de la izquierda corresponde a
un análisis experimental realizado en el Laboratorio y
la de la derecha a otro realizado en el concurso
Ciencia en Acción 2010,
donde mereció una Mención de Honor del Jurado. El
experimento utiliza una cámara para
filmar el movimiento y el
programa Modellus para simularlo y analizar la
correspondencia entre el movimiento real filmado y un
movimiento uniforme, simulado.
Clic aquí para consultar
estos experimentos. |
|
|
| |
|
|
|
