|
 |
|
CAÍDA DE UNA BOLA DENTRO DEL AGUA
1 (ANÁLISIS CON MODELLUS) |
|
|
|
Experimento
realizado por alumnos de Secundaria y de Bachillerato del IES Leonardo Da Vinci de Alicante
y en el concurso Ciencia en Acción, así como por profesores en
cursos de formación docente. |
|
|
| |
|
PLANTEAMIENTO DEL EXPERIMENTO.
HIPÓTESIS A CONTRASTAR |
|
|
|
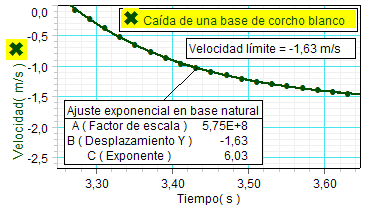
La gráfica procede
del estudio
con sensores
del
movimiento de
caída libre en el aire de un cuerpo ligero (una base
de corcho blanco), realizado en el laboratorio
del Instituto por alumnos de
1º Bachillerato. Como la fuerza
de rozamiento con el aire aumenta a lo
largo de la caída (dicha fuerza es proporcional a la
velocidad del cuerpo), la gráfica muestra que dicha
fuerza tiene una influencia creciente sobre la velocidad
de caída. Llegado un cierto
instante la suma de dicha fuerza de rozamiento y la fuerza
de empuje se equilibra con la fuerza contraria de la
gravedad
y desde ese momento el cuerpo prosigue la
caída con movimiento uniforme a la velocidad límite (en
este caso,
1.63m/s). |
|
 |
|
| |
|
Considerando este concepto,
nos planteamos analizar con Modellus
el movimiento de caída de una bola dentro del agua. Al tener en
cuenta que la
densidad del agua es mucho mayor que la del aire, planteamos a
modo de hipótesis, que la
bola alcanzará enseguida la velocidad límite y, en consecuencia,
esperamos que tenga un movimiento de caída uniforme
casi desde el inicio. |
|
| |
|
VIDEOS SOBRE CAÍDAS
DENTRO DEL AGUA |
|
|
|
Los dos videos situados más a la izquierda los filmaron alumnos de 1º
Bachillerato en el laboratorio del Instituto (en 2010 y
2012). En el primero de ellos, la bola tiene una
densidad muy próxima a la del agua y cae muy lentamente
dentro de ella, mientras que en el otro, la densidad de
la bola es bastante mayor y cae también bastante más
rápido. El tercer video, en orden de izquierda a derecha, se filmó
en la final del concurso
Ciencia en Acción 11, celebrada en Santiago de
Compostela en octubre de 2010 y el cuarto, situado en el extremo derecho de
la pantalla, lo filmó un equipo de profesores en un
curso de formación docente realizado en Valencia en
febrero de 2018. |
| |
|
|
| |
|
Puesto que se
quiere determinar la velocidad de caída de la bola
dentro de la probeta, todos los dispositivos
experimentales prevén adoptar como referencia de
longitudes una altura conocida y
visible a la filmación.
|
|
| |
|
ANÁLISIS
EXPERIMENTAL CON MODELLUS |
|
|
|
Para
realizar el análisis experimental, se comienza volcando el video sobre una página
de Modellus vacía y se escribe en la ventana reservada al modelo
físico matemático de la simulación la ecuación de un
movimiento uniforme.
|
| |
|
 |
|
Con la herramienta de medida que proporciona
el programa para medir longitudes sobre la pantalla se obtiene la equivalencia entre pixels y
m (usando como referencia, en este caso, la altura conocida de la probeta).
Al hacer correr la animación se constata un alto grado de concordancia
entre el movimiento de caída real de la bola
y el
movimiento uniforme de una bola virtual, lo que
viene a confirmar la hipótesis de que la bola de
plástico alcanza enseguida la velocidad límite y
,desde entonces, cae con una velocidad constante.
|
|
|
|
|
| |
|
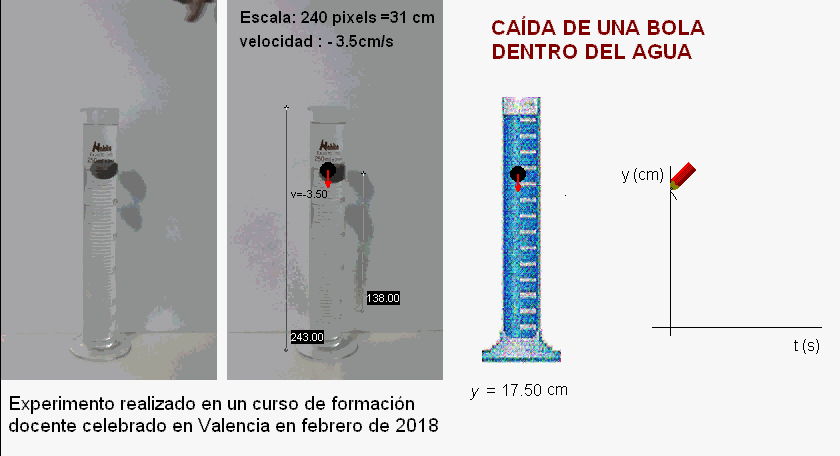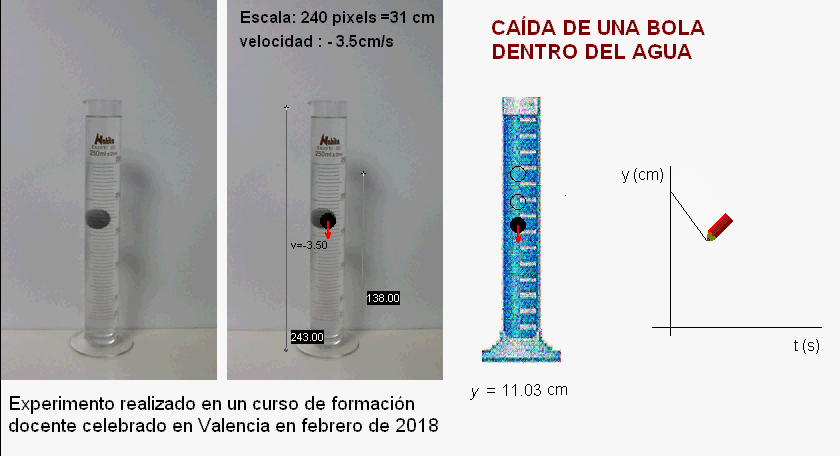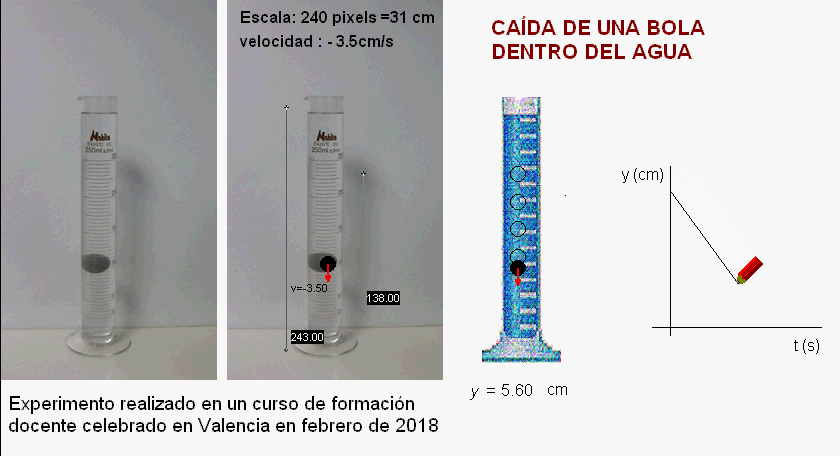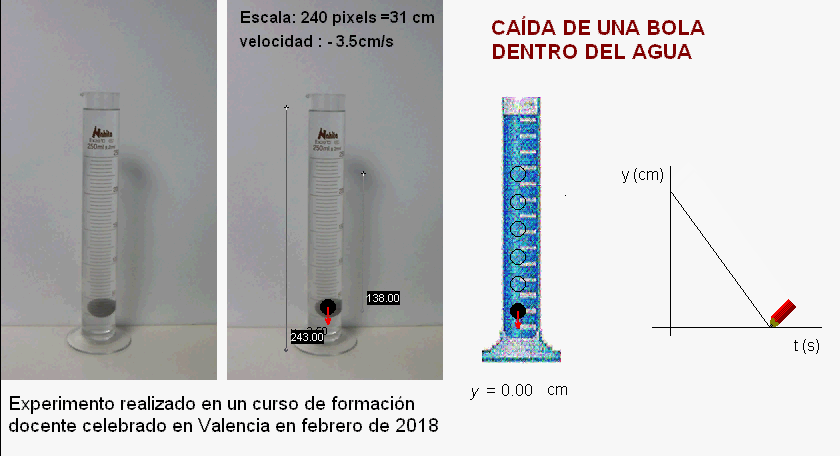Este otro ejemplo
corresponde a un curso de formación docente realizado en
Valencia en febrero de 2018. En este caso, los
profesores colocaron detrás de la probeta una plancha de
color gris que ayuda a aumentar el contraste, mejorando
la visualización de la caída de la bola. |
| |
|
 |
|
|
| |
|
|
En el otro experimento realizado
en el laboratorio con una bola metálica, el
movimiento de
caída es bastante
más rápido, pero se mantiene la concordancia entre el movimiento
de la bola y el movimiento uniforme de otra bola virtual. Por
tanto, la animación constata que también bola metálica alcanza
pronto la velocidad límite (de valor mucho mayor que la de la
bola de plástico) en su movimiento de caída dentro del
agua.
|
| |
|
Clic
aquí
descarga la animación (sólo
para
Modellus 2.5, 32 bits) |
|
|
 |
|
|
|
|
|
|
|
|
Finalmente diremos que en el experimento realizado
en Ciencia en Acción, 4 alumnos de Bachillerato
ofrecían a los visitantes participar en el
experimento, obtener el valor de la velocidad
constante de caída y llevarse la animación
(protagonizada por ellos) de recuerdo. |
|
|
|
|
| |
|
Ficha técnica del experimento en la Web de
Ciencia en Acción
|
|
|
|
