Ampliación del modelo de Bohr. Números cuánticos

AMPLIACIÓN DEL MODELO DE BOHR. NÚMEROS CUÁNTICOS

A pesar del gran avance logrado por el modelo de Bohr, su éxito tampoco fue muy duradero y casi inmediatamente después de su aplicación fue necesario revisarlo para atender a los resultados de los espectros atómicos. Los espectros de átomos poli-electrónicos ya habían evidenciado una estructura mucho más compleja en la que, en lugar de cada línea "gruesa" que podía corresponder a un nivel de energía del modelo de Bohr, se encontraba un conjunto de líneas más finas. Al utilizar espectroscopios más potentes, el espectro de Hidrógeno enseguida mostró que sus rayas espectrales también estaban desdobladas.

En 1916 Sommerfield (1868-1951) dio una interpretación de estos hechos proponiendo una mayor complejidad en la estructura electrónica que la que había considerado el modelo inicial de Bohr: "El desdoblamiento de las líneas espectrales se debe a que cada nivel de energía calculado a partir de los postulados de Bohr en realidad esta formado por varios subniveles". Relacionó esta propuesta con la suposición de que las órbitas del electrón podían ser elípticas y con diferentes excentricidades. 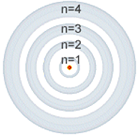Recordemos que el modelo de Bohr inicial utiliza un único parámetro, n, para caracterizar los niveles de energía permitidos del electrón. Este parámetro se llama número cuántico principal y puede tomar los valores: 1, 2, 3..., . Para cada uno de estos valores, se obtiene la energía y el radio de una órbita electrónica que se supone siempre circular.

Para tener en cuenta el desdoblamiento de las líneas espectrales iniciales del átomo de Hidrógeno, Sommerfield introdujo un segundo parámetro, l (número cuántico secundario), que puede tomar los valores los valores l = 0, 1, 2,…(n-1).

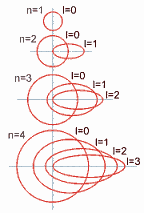
Así, para cada valor de n se permiten varias órbitas electrónicas de diferente excentricidad. Tal como se indica en la figura adjunta l=0 corresponde a la órbita circular, l=1 a la órbita elíptica menos excéntrica, l=2 a la siguiente, de mayor excentricidad que la anterior,.. (la excentricidad de una elipse aumenta cuanto mayor sea la separación entre sus dos focos; una circunferencia es una elipse de excentricidad nula, en la que coinciden los dos focos en el centro de la circunferencia).

Formalmente el número cuántico secundario se liga a una cuantización del momento cinético o cantidad de movimiento angular del electrón en su órbita, porque decir que el electrón sólo puede tener determinadas órbitas elípticas es lo mismo que afirmar que su momento cinético sólo puede tener determinados valores. Por ello, al número cuántico secundario se le denomina número cuántico del momento angular o número cuántico azimutal.

Los subniveles l = 0, 1, 2 y 3 se designan respectivamente con las letras s, p, d y f , derivadas de la terminología inglesa para la espectroscopía. Así, por ejemplo, 2s designa el subnivel de número cuántico principal 2 y número cuántico secundario 0, 3p designa el subnivel de número cuántico principal 3 y número cuántico secundario 1, etc.

Otros hechos iban a complicar aún más este modelo de Bohr-Sommerfield. En 1896, al estudiar la acción de campos magnéticos sobre los espectros de algunos gases, Zeeman (1865-1943), había descubierto el efecto que lleva su nombre: Las líneas espectrales de una fuente luminosa sometidas a un campo magnético intenso se dividen en varios componentes, cada uno de ellos polarizado. Este descubrimiento se enmarcaba en una investigación dirigida por su maestro, Lorentz (1853-1928), con el propósito de suministrar pruebas a favor de la teoría electromagnética de la luz. Además de contribuir a este objetivo, el efecto descubierto enseñó otra complejidad en la estructura del átomo. Para dar cuenta de dicha complejidad, se interpretó el desdoblamiento espectral considerando que un electrón girando alrededor de un núcleo es equivalente a una corriente eléctrica, y como tal produce un campo magnético perpendicular al plano en el que se mueve el electrón (es decir, es un pequeño imán). Al aplicar un campo magnético externo al átomo, ese imán electrónico se orienta.

Entonces, el hecho de que al aplicar el campo magnético al átomo la línea espectral se divida en un número determinado de ellas, indica que esa orientación de la corriente electrónica afectada por el campo magnético también está cuantizada, o, dicho de otro modo, indica que la corriente electrónica sólo puede tener determinadas orientaciones. Estas orientaciones permitidas dependen de la dirección en la que se aplica el campo magnético externo y de la corriente electrónica que lo sufre, la cual a su vez depende del momento angular del electrón y se caracteriza por el número cuántico azimutal, l.

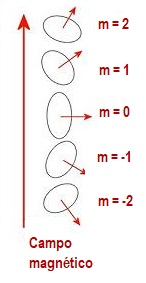
Usando estos razonamientos se introdujo un tercer número cuántico, m (número cuántico magnético), cuyos valores posibles dependen de l. El número magnético m puede tener todos los valores enteros entre -l y +l, incluyendo el cero. Así, por ejemplo, para l=2, m puede valer -2, -1, 0, 1, 2, lo que implica que el subnivel d se desdobla en otros 5. La figura adjunta representa estos 5 desdoblamientos sobre la imagen de una corriente electrónica equivalente a un pequeño imán.

En 1902 Zeeman y Lorentz, fueron galardonados con el Premio Nobel de Física por su investigación conjunta sobre la influencia del magnetismo en la radiación, originando la radiación electromagnética.

Con la introducción de los números azimutal y magnético se explicaban los tripletes (subnivel p) y quintupletes (subnivel d) del efecto Zeeman. Pero, se vio que el efecto Zeeman también presentaba otras colecciones de líneas, que no eran explicadas con estos números y se llamó efecto Zeeman anómalo. Se trata de dobletes que inicialmente se observaron en el subnivel s, donde l=0 y sólo debería haber un valor posible de m (m=0). Posteriormente se comprobó que estos dobletes ocurren en todos los subniveles y en 1925 Uhlenbeck (1900-1988) y Goudsmit (1902-1978) introdujeron un cuarto número cuántico, s (número cuántico de espín) para explicarlos. Este cuarto número tiene la particularidad de no relacionarse con la órbita ocupada en el átomo y hacerlo en cambio con una hipotética rotación del electrón sobre sí mismo (en inglés spin significa giro o girar).

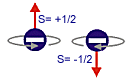
Imaginando al electrón como una partícula cargada que gira alrededor de un eje propio, se deduce que generará un campo magnético y se plantea que únicamente puede tener dos sentidos de giro posibles. A estos sentidos de giro de la hipotética rotación interna del electrón le corresponden dos posibles valores del espín: +1/2, -1/2, que más coloquialmente se denominan espín arriba o espín abajo.

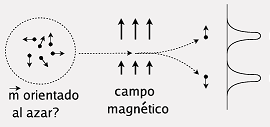
Una manera más formal de interpretar el espín es asignar al electrón un momento angular intrínseco. Con el desarrollo de la mecánica cuántica este concepto se extendió a todo tipo de partículas (aunque no tengan carga eléctrica) y se pudo comprobar mediante un notable experimento realizado en 1922 por Stern y Gerlach. En dicho experimento, un haz de átomos de plata era colimado por dos rendijas estrechas y atravesaba una bobina magnética.

La interacción del campo magnético producido por la bobina con el momento angular de los átomos de plata provoca que éstos se desvíen de su trayectoria. En principio, cada átomo podría tener cualquier orientación de su momento angular, sufriría una desviación distinta, y el haz se abriría de forma continua. Sin embargo, se observó que haz inicial se divide en dos haces perfectamente definidos, lo que indica que el momento angular intrínseco de los átomos sólo tiene dos orientaciones (por tanto, dos posibles valores del espín).