|
|
|
 |
|
PÉNDULO SIMPLE IV. ESTUDIO SOBRE LA INFLUENCIA DE LA LONGITUD |
|
|
| Experimento
realizado por alumnos de Secundaria en el IES "Leonardo Da Vinci" de Alicante
|
|
|
| |
|
|
|
|
|
|
|
|
|
HIPÓTESIS Y DISEÑO EXPERIMENTAL |
| |
| |
|
En los experimentos
realizados sobre la
influencia de otros factores en el periodo del
péndulo simple se ha puesto de manifiesto la
influencia de la longitud, cuyo estudio se
propone ahora específicamente. Se pretende
contrastar la
hipótesis que se emitió sobre de la influencia de
esta variable, según la cual al aumentar la
longitud, debería aumentar el periodo. |
|
|
|
Para ello, al
concretar un diseño experimental tenemos
en cuenta la no influencia de la masa
y el hecho de que la
influencia de la amplitud se puede
despreciar para oscilaciones de pequeña amplitud.
|
| |
|
 |
|
Considerando todo esto, se plantea a los
estudiantes que
determinen experimentalmente el periodo
del péndulo simple en oscilaciones
pequeñas y para longitudes
crecientes del mismo (de 5 en 5 cm). Una variante del
experimento puede consistir en que todos los
grupos midan el periodo que corresponde
a todas las
longitudes.
Otra alternativa es proponer
a cada equipo que determine el periodo
para una determinada longitud del
péndulo, de tal forma que entre todos se
complete el número de longitudes
previsto.
Los equipos pueden usar un
cronómetro ordinario para medir los
tiempos (tomados sobre un número amplio
de oscilaciones y con no menos de 3
mediciones de cada longitud) o, también, pueden
utilizar el sensor de fuerza para
determinar el periodo siguiendo el
procedimiento aprendido en el
estudio de la influencia de la amplitud. |
|
| |
|
|
|
|
| |
|
 |
| |
|
RESULTADOS |
| |
|
|
| |
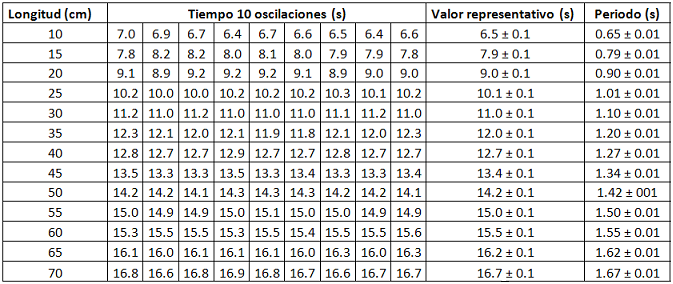
Se muestran resultados obtenidos en 3º ESO,
usando un cronómetro manual para medir el tiempo correspondiente
a 10 oscilaciones, del que se deriva el valor del periodo (una
oscilación). |
|
| |
|
|
| |
|
 |
|
En este caso
realizaron el experimento tres equipos de
alumnos.
Cada uno tomó un mínimo de 3 mediciones
del periodo para cada valor de la longitud, y, en la puesta en común, se
recogió finalmente el conjunto de las
9 medidas que refleja la
tabla adjunta.
Como se observa, un análisis
elemental de dicha tabla confirma la
esperada relación creciente entre la longitud y el periodo,
precisando que dicha relación no es lineal,
porque los incrementos sucesivos del periodo van
siendo menores para incrementos sucesivos de la
longitud iguales entre sí. |
|
|
|
|
|
|
| |
|
 |
| |
|
ANÁLISIS DE LOS RESULTADOS |
| |
|
|
| |
|
 |
|
 |
|
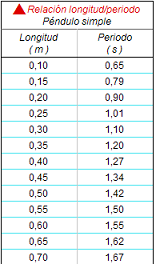
Analizados los resultados en
términos cualitativos se busca una posible relación
matemática entre la longitud y el periodo. Si se exige que al tender la longitud (l)
a cero, el periodo (T) también tienda a cero (lo que
equivale a obligar a
que la gráfica pase por el
origen), entonces, la relación entre la longitud
y el periodo puede ser exponencial: T = K· l n,
debiendo ser, en este caso, el exponente, n,
menor que la unidad.
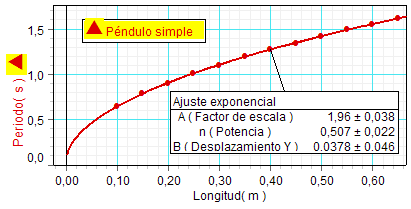
Así lo comprueban los
estudiantes después de realizar un ajuste exponencial sobre
la gráfica experimental, puesto que, de acuerdo con lo
dicho, dicho
ajuste proporciona un exponente muy próximo a
0,5. |
|
|
|
|
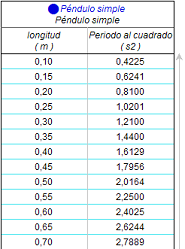
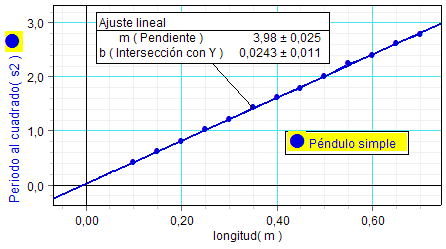
Por tanto,
este análisis indica
que, para oscilaciones de
amplitud pequeña, el
periodo y la raíz cuadrada de la longitud del péndulo
simple son proporcionales, lo
que se puede corroborar también
representando los valores de la
longitud frente a los
correspondientes del cuadrado
del periodo.
Como se
observa, dicha representación
produce una recta que
prácticamente pasa por el
origen. |
|
 |
|
 |
|
|
|
|
|
|
| |
|
 |
| |
|
PÉNDULO SIMPLE Y ACELERACIÓN DE LA GRAVEDAD |
| |
|
|
| |
|
Una consecuencia inesperada
que se extrae del estudio de
la relación entre la masa y el periodo del péndulo
simple es el hecho de que cuerpos de masa muy
diferente (como lo son las bolas de plástico y acero que
conforman los péndulos) caen igual. En 3º ESO los estudiantes
todavía no estudian
Dinámica newtoniana,
por lo que esta cuestión queda
planteada como un problema pendiente, que se investigará
en cursos posteriores. |
|
|
|
Ahora bien, en este nivel los
alumnos sí saben que la caída de los
cuerpos "se debe a la atracción de la Tierra" y algo han
oído hablar acerca de "la
gravedad", como un concepto que juega un papel principal en
los estudios acerca de dicha atracción gravitatoria. Por
tanto, entienden que es
razonable esperar que el periodo del péndulo simple se
relacione (además de con la longitud y con la amplitud)
con la aceleración de la
gravedad, g. De dicha relación se deriva que el
experimento que han realizado también pueda ser empleado para obtener
el valor de g. |
|
|
|
 |
|
|
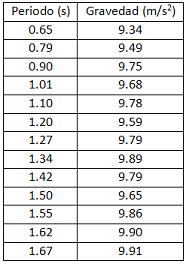
La
tabla adjunta muestra
los valores de la
aceleración de la
gravedad que se
calculan a partir de cada
valor experimental del
periodo obtenido en este
experimento. Como
la fórmula que obtiene
el periodo del péndulo
simple en función de las
variables influyentes
(longitud, l y
aceleración de la
gravedad, g) es: |
|
|
|
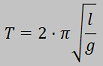 |
| |
|
Dichos valores de la
aceleración de la
gravedad se obtienen
usando directamente la
siguiente expresión: |
|
|
|
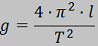 |
|
|
|
|
|
Para obtener un valor
representativo a partir de todos ellos
nos apoyamos en la representación
gráfica ya realizada sobre la relación
entre el cuadrado del periodo y la
longitud del péndulo. De acuerdo con la
fórmula del periodo, la pendiente de
dicha gráfica es: |
|
|
|
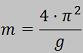 |
|
|
|
Y, por tanto, la
aceleración de la
gravedad se puede
calcular usando la
siguiente expresión: |
| |
|
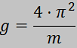 |
| |
|
Si se
consideran todos los
valores experimentales,
esta pendiente sería
3,98 s2/m,
lo que daría un valor de
g igual a 9,92 m/s2.
Este no es el mejor
valor de g que se puede
obtener con estos datos
experimentales.
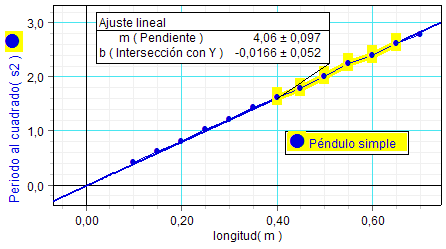
Para
optimizar el
procedimiento interesa
seleccionar un conjunto
más reducido de puntos
de la gráfica (gráfica
adjunta, a la
izquierda), escogidos de
forma que
la recta que los
ajusta sea la que pasa
más
próxima al
origen. Así, la pendiente
resulta 4,06 s2/m
y se obtiene un valor de g
igual a 9,72 m/s2. |
|
|
 |
|
|
|
|
|
|
| |
|
 |
| |
|
ANIMACIÓN DE REFUERZO |
| |
| |
|
 |
|
Al terminar el
estudio experimental sobre los factores
que influyen en el periodo del péndulo
simple, ofrecemos a los alumnos usar la
animación Modellus adjunta,
elaborada por el Departamento.
Dicha
animación simula el movimiento
de oscilación del péndulo simple y
calcula su periodo para oscilaciones
"relativamente pequeñas" (hasta 40º).
Permite modificar el ángulo inicial
(amplitud de las oscilaciones) y la
longitud del péndulo, comprobando cómo
afectan estos cambios al movimiento de
oscilación y al valor del periodo.
Finalmente, a modo de
resumen y ampliación de estos trabajos
sobre el péndulo simple, recomendamos la
lectura de
este documento en el que,
después de desarrollar con detalle todos
estos experimentos, se hace un repaso a
algunos aspectos de la teoría sobre el movimiento de
oscilación del péndulo.
Clic
aquí para descargar la animación.
Para usarla en tu ordenador necesitas
Modellus |
|
| |
|
|
|
|
| |
|
 |
