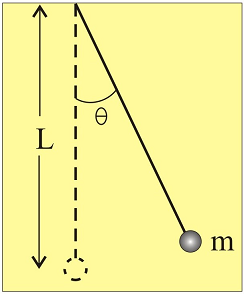Las hipótesis formuladas por la clase se resumen considerando tres magnitudes que pueden influir en el periodo (T) del péndulo simple: la masa del péndulo (m), la amplitud de las oscilaciones (representada por el ángulo inicial, q),  y la longitud del péndulo, L. Los alumnos plantean concretamente las siguientes hipótesis:

 

- En términos generales, suele haber una mayoría de estudiantes que piensa que, a igualdad de los restantes factores, cuanto mayor sea la longitud, L, mayor será el periodo, T, argumentando que una mayor longitud implica también un recorrido mayor en cada oscilación. - Sobre la influencia de la amplitud del péndulo simple, q, la opinión no es tan unánime. Algunos alumnos piensan que a mayor ángulo de oscilación, mayor será el periodo y lo suelen argumentar diciendo que un ángulo mayor implica que la longitud recorrida por la bolita también será mayor. Pero otros no lo tienen tan claro y señalan que a mayor ángulo también la bolita irá más rápida mayor sea la amplitud. - En cuanto a la masa, m, ocurre algo parecido, algunos piensan que cuanto mayor sea la masa, más pesará la bolita y asocian este mayor peso a bajar más rápido, lo que les lleva a pensar que el periodo será tanto menor cuanto mayor sea la masa. Pero también hay otros que señalan que si bien puede ser que baje más rápido, también subirá luego más lentamente…

El diseño experimental "tradicional"  usa un montaje como el que muestra la imagen adjunta para hacer oscilar al péndulo (también se pueden obtener resultados aceptables de forma aún más sencilla: sujetando el extremo superior del péndulo con dos dedos de una mano), que incluye una cinta métrica para medir la longitud del péndulo y un cronómetro para medir los tiempos. Existen, con este montaje, varios detalles de tipo técnico que es necesario tener en cuenta antes de comenzar la propia realización de los experimentos:

 

a) Hay que evitar la posibilidad de que el hilo resbale. Para que no ocurra, se ha de apretar bien la pinza que lo debe sujetar fuertemente por un único punto.   b) La longitud del péndulo deberá medirse desde el punto de suspensión hasta el centro de la bola (se puede determinar fácilmente sumando a la longitud del hilo el radio de ella)   c) Como el cronómetro se acciona manualmente, existe una imprecisión importante en la medida del tiempo (mayor que la propia sensibilidad del cronómetro). Además, el tiempo que dura cada oscilación es bastante "pequeño". Para solucionar estos problemas conviene medir el tiempo t que tarda el péndulo en realizar N oscilaciones completas y dividir dicho tiempo entre el número de oscilaciones realizadas, con lo que obtendríamos: T = t/N. Sin embargo, ello supone admitir implícitamente que el valor del ángulo de oscilación, q, no influye en el período. Por tanto, lo primero que hay que hacer es estudiar la posible dependencia de T con q.

Además de directamente sobre la gráfica, el periodo también se puede obtener realizando un ajuste sinusoidal de la misma. Esta segunda opción permite obtener de una sola lectura el periodo medio correspondiente a varias oscilaciones consecutivas.