|
|
|
 |
|
PÉNDULO SIMPLE II. ESTUDIOS SOBRE LA INFLUENCIA DE
LA AMPLITUD |
|
|
| Experimento
realizado por alumnos de Secundaria en el IES "Leonardo Da Vinci" de Alicante
|
|
|
| |
| |
 |
RESULTADOS OBTENIDOS USANDO UN MONTAJE TRADICIONAL |
 |
RESULTADOS OBTENIDOS USANDO EL SENSOR DE FUERZA |
 |
EL
PERIODO DEL PÉNDULO SÍ DEPENDE DE LA AMPLITUD |
 |
GALILEO Y HUYGENS |
|
|
|
|
|
|
|
|
| |
|
RESULTADOS
OBTENIDOS CON UN MONTAJE TRADICIONAL |
| |
| |
|
En la
primera parte de este trabajo práctico se
plantean varios diseños experimentales con los
que se puede
investigar acerca de los factores que pueden influir en el
periodo del péndulo simple. En el estudio sobre la posible influencia de la amplitud,
los equipos pueden iniciar los experimentos usando el montaje
tradicional, que usa una cinta métrica para
determinar la longitud del péndulo y un
cronómetro para medir el periodo de oscilación. Cada equipo puede utilizar un péndulo propio
y medir varias veces el periodo correspondiente a dos amplitudes
diferentes (en este caso, se hizo una con ángulo inicial
entre 30º y 35º, y la otra con ángulo inicial
entre 5º y 10º). |
| |
|
 |
|
La clase se sorprende
porque los resultados de la mayoría de
los grupos (como el ejemplo de la tabla
adjunta) aunque indican un periodo
algo mayor para la amplitud mayor
(en coincidencia con la hipótesis que
había formulado), también muestran que en todo
caso esta variación sería muy pequeña.
|
|
| |
|
Por ello, no se puede
extraer todavía una conclusión inequívoca, más teniendo
en cuenta la importante imprecisión que
tienen los resultados (recuérdese que el cronómetro se activa
manualmente) |
|
|
|
Intentando explicar por qué
la diferencia entre los valores del periodo para
amplitudes bastante diferentes resulta bastante menor de la esperada, algunos
alumnos pueden sugerir la idea
de que las
oscilaciones de mayor amplitud se baten a mayor velocidad que las de
menor amplitud. Indican que el hecho de que
la velocidad sea diferente
quizá compense al hecho de que la longitud recorrida
también lo es (en sentido opuesto). |
| |
|
|
|
|
| |
|
 |
| |
|
RESULTADOS
OBTENIDOS USANDO EL SENSOR DE FUERZA |
| |
| |
|
Con el sensor se puede
registrar la evolución de la tensión del péndulo
y habrá que hacerlo durante un tiempo bastante
amplio, para empezar a registrar oscilaciones
con un ángulo relativamente grande (unos 60º) y
terminar de tomar mediciones con un ángulo
pequeño (unos 5º o 10º). De la gráfica
correspondiente se pueden obtener valores del
periodo para las amplitudes cada vez menores con
las que va oscilando el péndulo a medida que se
amortigua su movimiento.
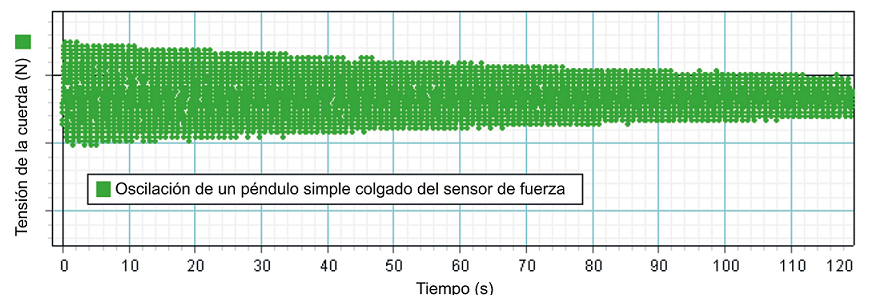
En este caso,
los alumnos
obtuvieron la siguiente gráfica: |
| |
|
 |
| |
|
En la que, como
vemos, se confirma la
esperada oscilación de la tensión de la
cuerda a medida que el péndulo oscila y
también se observa cómo las diferencias entre
la tensión máxima y la tensión mínima del péndulo
decrecen paulatinamente, a
consecuencia del progresivo amortiguamiento de las
oscilaciones (si hubiera dejado oscilar
al péndulo indefinidamente, habría
acabado en reposo en posición vertical y
en esa posición el módulo de la tensión
ya sería igual al módulo del peso de la
bolita). |
|
|
|
|
Seguidamente, obtuvieron el periodo de
oscilaciones de amplitudes paulatinamente
decrecientes seleccionando tramos que las
contienen y que estaban separados por intervalos
iguales de tiempo (en este caso, cada 20 s).
Recordemos que cada oscilación se corresponde
con un recorrido completo de ida y vuelta del
péndulo y, por tanto (como ya hemos visto),
abarca a tres máximos consecutivos (o tres
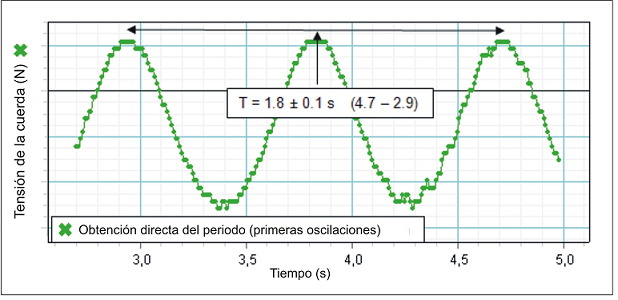
mínimos) de la gráfica. Las imágenes siguientes
muestran dos de estas mediciones: |
| |
|
 |
|
Como vemos, en las
oscilaciones iniciales (es decir, las de
mayor amplitud) se obtuvo un periodo: T
= (1,8 ± 0,1) s. |
|
| |
|
 |
|
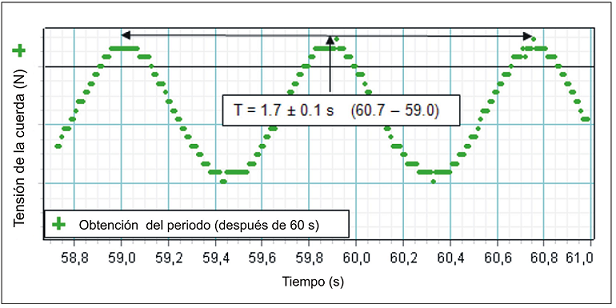
Y en oscilaciones
posteriores, ocurridas después de dejar
oscilar al péndulo durante
aproximadamente un minuto (por tanto, de
bastante menor amplitud que las
primeras) se obtuvo un periodo: T= (1,7
± 0,1) s |
|
| |
|
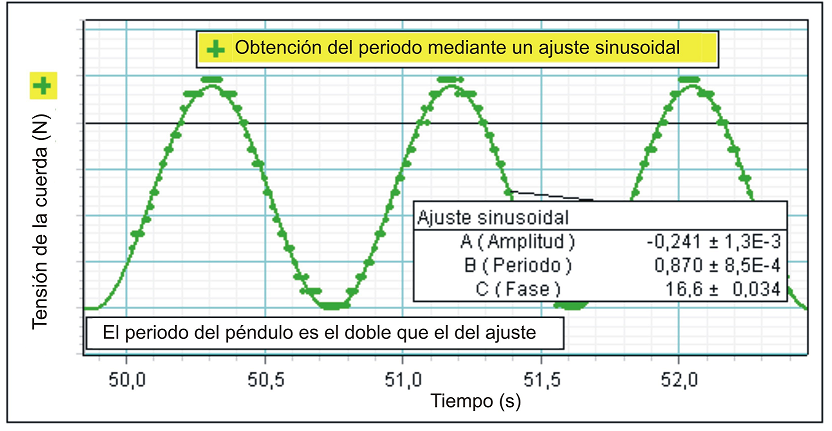
Estos mismos resultados, se
pueden obtener (con mayor precisión) realizando
con el programa un ajuste sinusoidal en las
gráficas, ya que dicho ajuste proporciona los
tres parámetros básicos de la oscilación
registrada por el sensor (amplitud, periodo y
fase). Al usar este procedimiento, hay que tener
en cuenta, una vez más, que el periodo de la
oscilación en la tensión de la cuerda (que es lo
que mide el sensor) es exactamente igual a la
mitad del periodo de una oscilación completa del
péndulo simple. |
| |
|
 |
| |
|
|
|
|
| |
|
 |
| |
|
EL
PERIODO DEL PÉNDULO SÍ DEPENDE DE LA AMPLITUD |
| |
| |
|
Los resultados obtenidos con el sensor,
indican que, aunque en un grado mucho menor que
el esperado, el periodo del péndulo simple depende de la amplitud. Y así es en efecto, como
confirman, no sólo los estudios experimentales
de alta precisión, sino también la propia teoría
del péndulo simple. |
| |
|
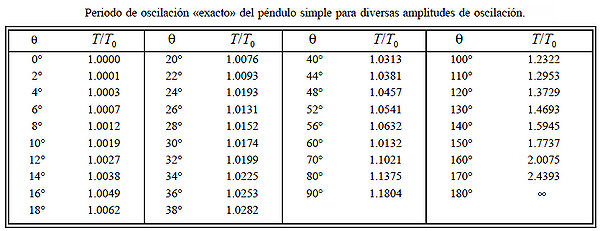
De hecho, la solución de la ecuación
del movimiento del péndulo para
oscilaciones de cualquier amplitud
proporciona valores que se van separando
cada vez más de la solución aproximada
que podríamos considerar si la amplitud no influyera.
La tabla adjunta aporta los
valores del cociente entre el periodo
real o "exacto" de las oscilaciones (T) y el
periodo que
tendrían (To),
si siempre fuera correcta la solución
aproximada (Fuente:
Wikipedia). |
|
 |
|
| |
|
Dicho cociente es
muy próximo a la unidad para ángulos pequeños y,
por eso, para oscilaciones de pequeña amplitud
es legítimo considerar el periodo casi
constante. |
| |
|
|
|
En los laboratorios
de los institutos se pueden
obtener resultados bastante
fiables del incremento del
periodo con la amplitud, sin necesidad
de utilizar tecnología avanzada, como
son los propios sensores de fuerza.
A
modo de ejemplo, recomendamos
el
este trabajo de Luís Ignacio
García, realizado en 2º
Bachillerato (incluye una hoja Excel
muy útil para que los alumnos recojan y
analicen los resultados). Esto, no obstante,
sobrepasa el objetivo de este trabajo
práctico, realizado en 3º ESO, donde sí
informamos a los alumnos del aumento
real del periodo con la amplitud, les
mostramos la gráfica teórica que refleja
dicho aumento y también la tabla de
valores anterior. Usándola realizan (con
nuestra ayuda) algunos cálculos
sencillos, que explican por qué en su
estudio experimental pasa casi
inadvertida la dependencia del periodo
con la amplitud. |
|
| |
|
|
|
|
| |
|
 |
|
|
|
GALILEO Y HUYGENS |
| |
| |
|
Como complemento a este
estudio sobre la influencia de la
amplitud en el periodo del péndulo simple, se
puede pedir a los alumnos que realicen un
trabajo bibliográfico acerca de
las aportaciones que hicieron Galileo y Huygens
en relación con el péndulo simple. |
| |
|
 |
|
En cualquier libro
(o en Internet), se puede encontrar el relato de
la leyenda, según la cual Galileo, un domingo de
1583, cuando era un estudiante de apenas 18
años, se distrajo en la catedral de Pisa al
observar el movimiento oscilatorio de una gran
lámpara colgante suspendida del techo.
Galileo
se sorprendió al ver que el candelero parecía
batir tiempos iguales, fuera cual fuese la
amplitud de las oscilaciones y, supuestamente,
cuando terminó la misa corrió a su casa, donde
ató distintas pesas en el extremo de varias
cuerdas para repetir la experiencia. |
|
| |
|
Cronometró las oscilaciones, utilizando como
patrón de medida del tiempo su propio pulso (en
aquella época no se disponía de cronometro
alguno para medir con un mínimo de precisión el
tiempo) y confirmó que la amplitud apenas
influye en el periodo.
Sea o no verdadera esta leyenda, lo que sí
parece ser cierto es que Galileo sugirió
utilizar un péndulo de una longitud dada para
medir el pulso de los pacientes (este aparato,
conocido como el "pulsómetro", se hizo muy
popular en la medicina) y que también se planteó
construir un reloj de péndulo, pero no lo
consiguió precisamente porque, como hemos vsito, el periodo del
péndulo simple en realidad sí depende de la
amplitud, aunque esa influencia sea
prácticamente insignificante cuando se manejan
ángulos pequeños. |
| |
|
 |
|
|
Más de 70 años
después, en
1657, Christian Huygens realizó el sueño de
Galileo, aplicando con éxito el péndulo a un
reloj. Huygens diseñó un reloj basado en la curva
cicloide (curva que describe un
punto de una circunferencia que
rueda a lo largo de una recta
horizontal). |
| |
|
 |
|
|
|
|
|
En su libro
Horologium oscillatorium,
publicado en 1637, dice "El péndulo simple no puede
ser considerado como una medida del tiempo
segura y uniforme, porque las oscilaciones
amplias tardan más tiempo que las de menor
amplitud; con ayuda de la geometría he
encontrado un método, hasta ahora desconocido,
de suspender el péndulo; pues he investigado la
curvatura de una determinada curva que se presta
admirablemente para lograr la deseada
uniformidad. Una vez que hube aplicado esta
forma de suspensión a los relojes, su marcha se
hizo tan pareja y segura, que después de
numerosas experiencias sobre la tierra y sobre
el agua, es indudable que estos relojes ofrecen
la mayor seguridad a la astronomía y a la
navegación. La línea mencionada es la misma que
describe en el aire un clavo sujeto a una rueda
cuando ésta avanza girando; los matemáticos la
denominan cicloide, y ha sido cuidadosamente
estudiada porque posee muchas otras propiedades;
pero yo la he estudiado por su aplicación a la
medida del tiempo ya mencionada, que descubrí
mientras la estudiaba con interés puramente
científico, sin sospechar el resultado."
|
|
 |
|
| |
|
 |
|
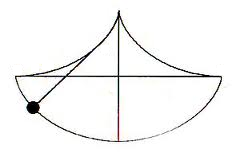
El
péndulo simple cicloidal
se concibe suspendiendo el hilo
entre dos contornos sólidos que tienen
la forma de arcos de cicloide tangentes
en su punto de unión.
Al oscilar el
péndulo, el hilo se ha de ceñir a uno u otro de
esos dos contornos cicloidales, de al
modo que la
longitud efectiva del péndulo queda
disminuida en una proporción que depende
de la amplitud de las oscilaciones. Huygens demostró que si la
circunferencia que genera los dos
contornos tiene un radio igual a la
cuarta parte de la longitud del hilo de
suspensión del péndulo, entonces el
péndulo describe un arco de cicloide y
es rigurosamente isócrono. |
|
| |
|
|
|
|
|
|
|
 |